一种双基地MIMO雷达的相关目标定位方法
王伟,王咸鹏,盖猛
(哈尔滨工程大学 自动化学院,黑龙江 哈尔滨150001)
0 引言
多输入多输出(MIMO)雷达是借鉴通信领域的多输入多输出技术而提出的一种新体制雷达[1-4],是最近几年在雷达领域研究的一个热点问题,具有广泛的应用前景。与传统的雷达相比,MIMO 雷达利用空间分集技术克服目标的闪烁特性[1-2],利用信号分集技术形成很大的虚拟阵列孔径[3-4],提高了目标的空间分辨力和探测性能。
目前MIMO 雷达的研究主要集中在MIMO 雷达的角度估计技术[5]、波束形成技术[6]以及目标成像技术[7]。在双基地MIMO 雷达中,估计出空中目标相对于发射阵列的发射角和相对于接收阵列的接收角,可以根据这两个角度的交叉点对目标进行定位。文献[8]提出了基于Capon 算法的发射角(DOD)和接收角(DOA)联合估计的方法,实现了双基地多个目标交叉侧向定位,文献[9]提出了二维旋转不变子空间(ESPRIT)算法在联合DOD 和DOA 估计中的应用。但由于这些方法需要二维空间处理,计算量庞大,不利于实时处理。文献[10]把双基地MIMO 雷达的二维方位角同时估计问题转化为两个一维方位角估计问题,然后采用两次ESPRIT 算法估计出目标的DOD 和DOA,不需要二维空间谱搜索,但需要对数据协方差矩阵进行特征值分解以及对DOD 和DOA 进行配对。文献[11]提出了一种自动配对的ESPRIT 算法,避免了配对算法的额外计算量。文献[12]提出了一种有效抑制色噪声联合DOD 和DOA 算法,把虚拟阵列划分成两个互不重叠的子阵,通过两个虚拟子阵输出数据的互协方差矩阵来抑制空间色噪声的影响,然后再利用ESPRIT算法实现发射角和接收角的联合估计。文献[13]中采用多项式求根技术实现了联合DOD 和DOA 估计,避免了空间谱搜索,计算量很小,有利于实时处理。文献[14]中指出当空间存在相关目标时,以上算法对于相关目标均失效,无法估计出目标的DOD和DOA.针对该问题,文献[15]提出了一种基于空间前向空间平滑(FSS)算法的相关目标联合角度的估计,但是该算法损失了MIMO 雷达虚拟阵列孔径,估计性能也相应的损失。
本文提出一种双基地MIMO 雷达相关目标的定位方法。该方法在MIMO 雷达发射端和接收端分别构造虚拟阵列,实现相关目标的解相关,然后进行DOD 和DOA 联合估计,且估计的二维参数自动配对,最后利用DOD 和DOA 的交叉点对相关目标进行定位,得到空间相关目标的位置。与前后向空间平滑算法相比,本文算法避免了阵列孔径损失,提高了目标的角度估计性能。仿真结果表明该算法的有效性和良好的估计性能。
1 双基地MIMO 雷达信号模型
如图1所示为双基地MIMO 雷达结构,发射阵列和接收阵列均为均匀等距线性阵列,所有的天线均为全向天线,有M 个发射阵元和N 个接收阵元,dt和dr分别为发射和接收阵元距。各个发射阵元同时发射同频正交的周期相位编码信号,其中发射信号满足以下条件:

其中:si和sj分别为第i 个和第j 个发射阵元的信号;L 为每个周期内的相位编码个数。假设多普勒频移对于信号的正交性没有影响;目标和发射阵元、接收阵元的距离远远大于发射阵列孔径和接收阵列孔径。

图1 双基地MIMO 雷达结构Fig.1 Principle diagram of bistatic MIMO radar
若在相同分辨距离单元上存在P 个目标,第i个目标相对发射阵元的发射角为θti(i =1,2,…,p),相对接收阵元的接收角为θri(i =1,2,…,p),其中(θri,θti)为第i 个目标的位置。接收阵列接收到的信号可表示为
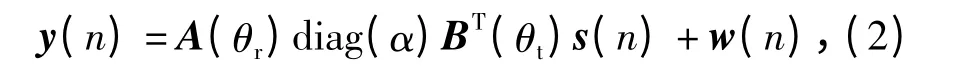
其中:y(n)=[y1(n),y2(n),…,yN(n)]T为接收阵列输出矢量;(·)T表示矢量或者矩阵的转置;diag(α)表示由矢量α=[α1,α2,…,αp]构成的p×p对角矩阵,其中,αi(i =1,2,…,p)为第i 个目标的散射系数;A(θr)=[a(θr1),a(θr2),…,a(θrp)],其中,a(θr)=[1,e-j(2π/λ)drsinθr,…,e-j(2π/λ)(M-1)drsinθr]T为N ×1 维的接收阵列导向矢量,λ 为载波波长;B(θt)=[b(θt1),b(θt2),…,b(θtp)],b(θt)=[1,e-j(2π/λ)dtsinθt,…,e-j(2π/λ)(M-1)dtsinθt]T为M×1 维的发射导向矢量;s(n)=[ej2πf1d,ej2πf2d,…,ej2πfpd]T为散射信号,fi(i=1,2,…,p)为第i 个目标的多普勒频率。w(n)为零均值平稳白噪声,假设它与信号相互独立。
发射信号均为正交信号,根据式(1)接收阵列在l 个重复周期内接收信号与发射信号进行匹配,第m 个匹配滤波器输出数据可以表示为

其中:bm(θt)为发射阵元的导向矢量中第m 个元素;wm(t)为第m 个匹配滤波器中的噪声矢量。因此经过M 个匹配滤波器滤波,接收阵列接收到的数据为

也可以表示为
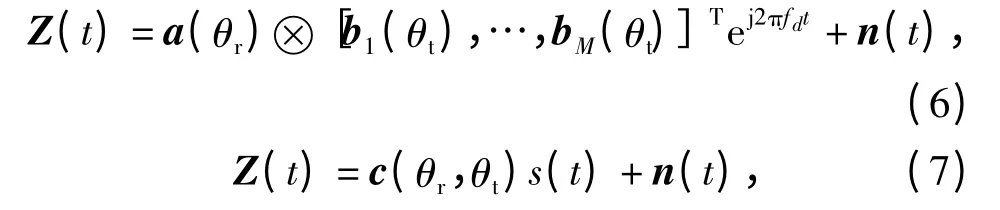
其中:c(θr,θt)=a(θr)⊗b(θt)为MN ×1 维导向矢量;n(t)为高斯白噪声;s(t)=ej2πfdt为单个目标信号。⊗表示Kronecker 乘积。
若空间有P 个目标时,匹配滤波后接收信号表示为

其中:C=[c(θr1,θt1),c(θr2,θt2),…,c(θrp,θtp)]为MN×P 的p 个目标导向矢量;c(θri,θti)=a(θri)⊗b(θti),S(t)=[α1ej2πf1t,α2ej2πf2t,…,αpej2πfpt]T为P个目标散射回来的信号。若p 个目标中有q(q =2,3,…,p)个目标散射信号具有相同的多普勒频率且为同一相位编码信号,那么这些目标是相关的。
由于MIMO 雷达DOD 和DOA 联合估计的算法需要对接收数据的协方差矩阵进行特征值分解,在目标相关情况下,对接收数据的协方差矩阵进行特征值分解会导致信号子空间信息“扩散”噪声空间,使噪声子空间与信号子空间无法正交,导致很多现有的算法无法正确估计这些相关目标的空间位置。本文提出一种相关目标条件下的定位方法,即在MIMO 雷达的发射端和接收端同时构造虚拟阵列,对相关目标散射信号解相关,恢复接收数据协方差矩阵的秩,然后再进行目标的DOD 和DOA 联合估计。
2 一种相关目标定位方法原理
由式(8)可知,MIMO 雷达的导向矢量相当于一个MN×1 个虚拟阵列接收的导向矢量,有两个相关目标散射回来接收信号为
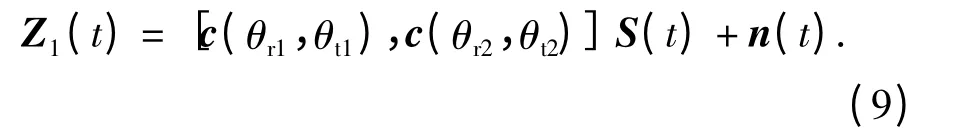
其中,c(θr,θt)=a(θr)⊗b(θt)为MN ×1 维导向矢量。
对于两个相关目标,在接收端和发射端分别构造的第k(1≤k)个虚拟矩阵为

那么Ar和At可表示为
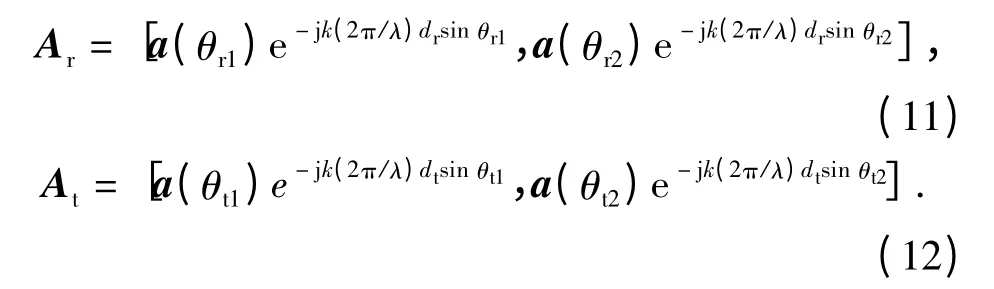
因此第k 个虚拟阵列的导向矢量为

其中:
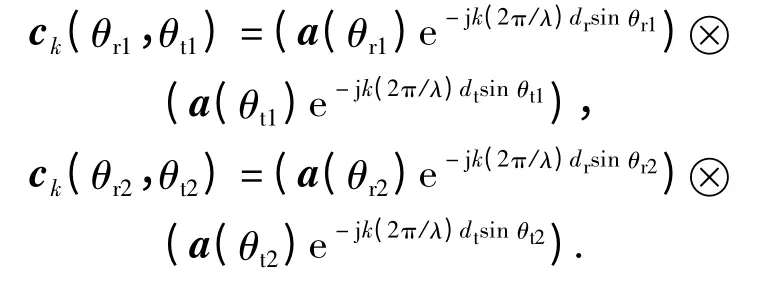
根据Kronecker 乘积的性质:
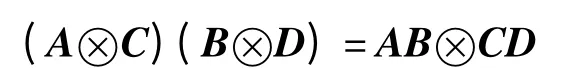
则有
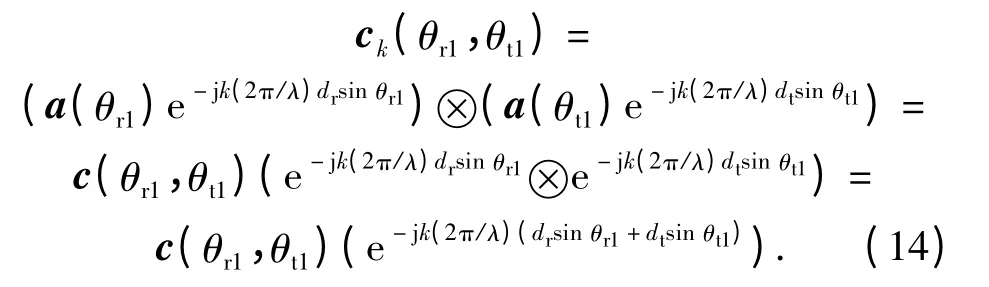
同理可得

则有
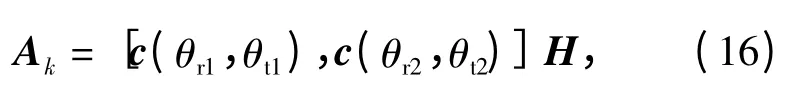
其中,

由式(16)可以知道,对于两个相关目标,这里等价于将MIMO 雷达经过匹配滤波器形成的虚拟阵列通过第k 次虚拟平移构成了第k 个虚拟阵列。由文献[16]可知,当虚拟平移的次数k 大于等于相关目标时,平滑后形成的虚拟阵列协方差矩阵的秩恢复到满秩,从而实现相关目标的解相关。这里为两个,则只需要构造两个虚拟阵列就可以实现对两个相关目标的解相关。
同理,若空间存在p 个相关目标,那么相应的第k 个虚拟阵列导向矢量为

MIMO 雷达的第k 虚拟阵列的接收数据为

其中,nk(t)第k 虚拟阵列中的噪声。
对MIMO 雷达接收的Z(t)和Zk(t)经过有限次初等变换[17]得到一组新的数据

其中,T 为MN×MN 的有限次初等行变换矩阵。
由式(8)和式(19)可得MIMO 雷达接收数据的互协方差矩阵为
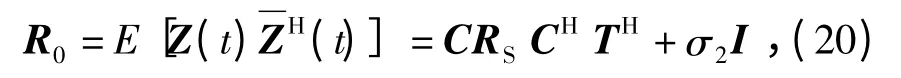
其中,RS=E[S(t)SH(t)].
由式(14)MIMO 雷达的第k(1≤k≤p)虚拟阵列的接收数据的协方差矩阵为

定义一个维数为的MN×MN 反对角置换矩阵

由式(20)、式(21)和式(22)得到相应数据协方差矩阵的修正矩阵

相关目标的散射信号经过虚拟阵列的协方差矩阵为

对式(24)的协方差矩阵进行奇异值分解为

其中:Us和Vs分别是MIMO 雷达虚拟阵列和经过式(19)初等行变换后新阵列的数据的信号子空间,VS=TUS;Un和Vn分别是MIMO 雷达虚拟阵列和经过式(19)初等行变换后新阵列的数据的噪声子空间,Vn=TUn;Σs为的特征值组成的对角矩阵,Σn为小特征值组成的对角矩阵,由ESPRIT 算法原理可以将US分割成Us1和Us2,将VS分割成Vs1和Vs2,其中Us1和Us2分别为Us的前M(N-1)行和后M(N-1)行,Vs1和Vs2分别是Vs的前N(M-1)行和后N(M-1)行,则有
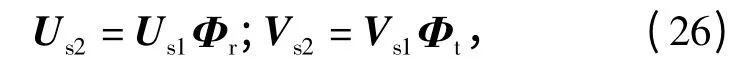
其中:Φr=B-1φrB,Φt=K-1φtK,其中B 和K 分别为Φr和Φt的特征向量组成的相似变换矩阵,φr和φt分别为Φr和Φt的特征值组成的对角矩阵,也就是ESPRIT 算法的旋转不变因子,对角线元素为方位角的参数信息。因此可以通过特征值分解Φr和Φt得到目标相应的方位角,但是方位角参数不能自动配对。
根据矩阵、矩阵特征值和特征值对应的特征向量三者之间的关系,使发射角和接收角度配对[9]



令rri为对角矩阵φr的第i(i =1,2,…,p)个对角元素,那么第i(i=1,2,…,p)目标相对于发射阵列的发射角和接收阵列的接收角估计值分别为

3 仿真及性能分析
为了验证算法的解相干特性以及估计性能,设计了3 组仿真实验。双基地MIMO 雷达发射和接收阵列的阵元距均为半个波长,各个发射阵元同时发射相互正交的Gold 码调相信号,每个周期内码元个数为K=127,码元宽度τ =400 ns,选取250 个周期内的回波信号。接收阵元数N=6,发射阵元数M=3.
实验一:本文算法和ESPRITI 算法对相关目标的联合角度估计性能对比
设空间存在3 个相关的目标,设它们相对于发射阵列的发射角和接收阵列的接收角分别为C(θr1,θt1)=(10°,-50°),C(θr2,θt2)= (-20°,10°),和C(θr3,θt3)=(30°,20°);3 个相关目标的信噪比均为0 dB.图2为文献[9]中的自动配对的ESPRIT 算法和本文算法对相关目标联合角度估计的参数星座图。从图2中可知,ESPRIT 算法无法正确估计相关目标的位置,本文算法可以正确的估计出多个相关目标的位置,且目标参数准确的自动配对。

图2 本文算法和ESPRITI 算法对相关目标的联合角度估计性能Fig.2 The targets localigation of proposed method and ESPRIT
实验二:本文算法和基于前向空间平滑(FSS)算法对相关目标的联合角度估计性能的比较
设空间存在2 个相关目标,它们相对于发射阵列的发射角和接收阵列的接收角分别为C(θr1,θt1)=(30°,20°),和C(θr2,θt2)=(-20°,10°),两个目标的信噪比相等。定义目标发射角估计均方根误差为

定义相关目标接收角的均方根误差为

实验三:目标方位角估计性能与相关目标数的关系

图3 目标发射角估计性能的比较Fig.3 The RMSE of DOD with different SNR
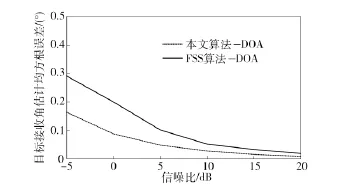
图4 目标接收角估计性能的比较Fig.4 The RMSE of DOA with different SNR
设空间相关目标的信噪比均为0 dB,定义相关目标发射角的均方根误差和接收角的均方根误差定义和实验二一样。图5为相关目标数和目标方位角度估计均方根误差的关系图,从图中可以看出,在所有相关目标均为0 dB 时,随着相关目标的增加,本文算法对相关目标的发射角度的估计均方根误差保持在0.2°左右,对相关目标的接收角度的估计均方根误差保持在0.1°左右。因此本文算法对于多个相关目标估计性能稳定。

图5 相关目标数与目标方位角估计性能的关系Fig.5 The RMSE of angle estimation with different targets
由仿真实验可知,本文方法通过在发射端和接收端分别构造出解相关的虚拟阵列,不损失发射端和接收端的阵元,保持了MIMO 雷达的分辨率,能够同时对多个空间相关目标解相关,正确的估计出目标的位置,对多个目标的估计性能良好且稳定。
4 结论
本文提出一种双基地MIMO 雷达的相关目标定位方法,通过在MIMO 雷达的发射端和接收端构造虚拟阵列,在不损失MIMO 雷达孔径情况下实现了对空间多个目标的解相关,估计出相关目标的空间位置,且估计性能稳定,同时估计参数自动配对,是一种能够实现空间多个相关目标定位的算法。理论分析和仿真结果验证了该算法的有效性。
References)
[1] Fisher E,Haimovich A,Blum R S,et al.Spatial diversity in radars-models and detection performance[J].IEEE Transactions on Signal Processing,2006,54(3):823-838.
[2] Haimovich A M,Blum R S,Leonard J,et al.MIMO radar with widely separated antennas[J].IEEE Signal Processing Magazine,2008,25(1):116-129.
[3] BekkermanI,Tabrikian J.Target detection and localization using MIMO radars and sonars[J].IEEE Transactions on Signal Processing,2006,54(10):3873-3883.
[4] Jian L,Stoica P.MIMO radar with colocated antennas[J].IEEE Signal Processing Magazine,2007,24(5):106-114.
[5] 夏威,何子述,廖羽宇.MIMO 雷达最大似然参数估计[J].中国科学F 辑,2011,42(2):234-345.XIA Wei,HE Zi-shu,LIAO Yu-yu.On the maximum likelihood method for target localization using MIMO radars [J].Scientia Sinica(Informationis),2011,42(2):234-345.(in Chinese)
[6] 郑志东,张剑云.MIMO 雷达波束方向图及其旁瓣抑制方法[J].系统工程与电子技术,2010,32(2):287-290.ZHENG Zhi-dong,ZHANG Jian-yun.Beam pattern and side-lobe suppression based on MIMO radar[J].Systems Engineering and Electronics,2010,32(2):287-290.(in Chinese)
[7] 王怀军,粟毅,朱宇涛,等.基于空间谱域填充的MIMO 雷达成像研究[J].电子学报,2009,36(6):1242-1246.WANG Huai-jun,SU Yi,ZHU Yu-tao,et al.MIMO radar imaging based on spatial spectral-domain filling[J].Acta Electronica Sinica,2009,36(6):1242-1246.(in Chinese)
[8] Yan H,Li J,Liao G.Multitarget identification and localization using bistatic MIMO radar systems[J].EURASIP Journal on Advances in Signal Processing,2008,8(2):1-8.
[9] Miao H,Juntti M,Yu K.2-D unitary ESPRIT based joint DOA and DOD estimation for MIMO system[C]∥IEEE 17th International Symposium on Personal,Indoor and Mobile Radio Communications,2006:1-5.
[10] DuoFang C,Baixiao C,Guodong Q,Angle estimation using ESPRIT in MIMO radar[J].Electrons Letters,2008,44(12).
[11] CHEN Jin-li,GU Hong,SU Wei-min.Angle estimation using ESPRIT without pairing in MIMO radar[J].Electronics Letters,2008,(44):1422-1423.
[12] Chen Jinli,Gu Hong,Su Weimin.An new method for joint DOD and DOA estimation in bistatice MIMO radar[J].Signal Processing,2010,90(2):714-718.
[13] Mohamed Laid Bencheikh,Yide Wang,Hongyang He.Polynomial root finding technique for joint DODA DOD estimation in bistatic MIMO radar[J].Signal Processing,2010,90(2):2723-2730.
[14] Jian Li,Petre Stoica.MIMO radar signal processing[M].John Wiley & Sons,Inc.,2009:167-168.
[15] Zhang Yongshun,Guo Yiduo,Niu Xinliang,et al.Angle estimation of coherent multi-target for MIMO bistatic radar[C]∥International Conference on Image Analysis and Signal Processing,2010:146-149.
[16] Pillai S U,Kwon B H.Forward/backward spatial smoothing techniques for coherent signal identification[J].IEEE Transactions Acoust.Speech Signal Process,1989,37(1):8-15.
[17] Tang Ming,Wang Ding-jiang,Feng Ming,et al.Linear algebra[M].Hangzhou:Zhejiang University Press,2004:50-56.

