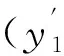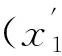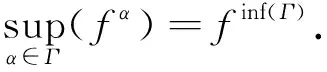效应代数上的模糊滤子

王 敏, 曹怀信, 张坤利

(陕西师范大学 数学与信息科学学院, 陕西 西安 710062)

0 引言

效应代数是由Foulis和Bennett于1994年引入的一种代数结构. 随着量子逻辑研究的发展,关于其代数结构的研究引起了人们的广泛关注. 近年来, 许多学者提出了一些新的代数结构作为研究量子逻辑的模型. 效应代数包含了量子逻辑中经常研究的情形(正交模格和偏序集).

1994年, Foulis在文献[1]中研究了局部滤子并给出了一些重要性质. 后来, Wu Jing在文献[2]中提出了理想和滤子的概念. 模糊滤子之所以重要是因为它包含了经典滤子. 徐扬和秦克云在文献[3]中研究了模糊格蕴涵代数与模糊滤子. 近年来, 相关方面的研究越来越多. 李海洋和李生刚于2008年在文献[4]中研究了伪效应代数中的同余和理想, 并引入了Riesz强同余的概念. 刘东利和王国俊于2009年在文献[5]中引入了效应代数中模糊滤子和模糊理想的概念并研究了它们的一些性质, 引入并研究了强模糊滤子. 在全序效应代数中提出了一个模糊同余关系并证明了这样生成的同余类是一个全序格效应代数. 在此基础上, 本文进一步研究模糊滤子的性质, 引入了正规模糊滤子的定义, 并给出了模糊滤子可以诱导出效应代数的同余关系.

在本文中E是一个效应代数.

1 效应代数的模糊滤子

定义1[5]F是E的非空子集, 如果F满足下列条件, 则称F是E的滤子.

(1)若a∈F, 则b∈E,a≤b,则b∈F；

(2)若a∈F,b∈E,b≤a,则a′⊕b∈F；

映射f：E→[0,1]称为E的模糊子集, 记f′=1-f, 对任意x∈E, 定义(1-f)(x)=1-f(x).记FI(E)为E中所有滤子之集，则易知FI(E)是一完备格.

定义2[5]E的模糊子集f如果满足下面条件, 则称f为E的模糊滤子

(F1)任意x,y∈E, 若x≥y, 则f(x)≥f(y)；

(F2)任意x,y∈E, 若x≥y, 则f(y)≥f(x′⊕y)∧f(x).

事实上, 由(F1)成立容易验证(F2)等价于(F2′):

(F2′)任意x,y∈E, 若x≥y, 则f(y)≥f(x′⊕y)∧f(x).

进而, 我们可以从(F2′)得到(F1). 所以若f只满足(F2′), 则f仍是E的模糊滤子.

记F(E)为E中所有模糊滤子之集, 易验证, 若干个模糊滤子的交集仍是模糊滤子. 若f是E的一个滤子, 令〈f〉=∩{g|g是E的一个模糊滤子且f⊆g}, 则〈f〉是包含f的最小模糊滤子, 称为由f生成的模糊滤子.

易知F(E)是一个完备格, 其中对于任意f,g∈F(E),f∧g=f∩g,f∨g=〈f∪g〉.

定理1 设f是E的一个滤子, 则对任意x∈E,〈f〉(x)=sup{t|t∈[0,1]且x∈〈ft〉}

证明 设g是E的一个滤子,对任意x∈E,

g(x)=sup{t|t∈[0,1]且x∈〈ft〉}

(1)以下证明g是E的一个模糊滤子. 对于任意x∈E,

g(1) =sup{t|t∈[0,1]且1∈〈ft〉}

≥sup{t|t∈[0,1]且x∈〈ft〉}

=g(x)

若存在x,y∈E且x≥y,使

g(y)

=min{g(x),g(x′⊕y)},

则

g(y)

g(y)

从而存在t0,t1∈[0,1], 使x∈〈ft0〉，x′⊕y∈〈ft1〉且g(y)

(2)以下证明f⊆g. 对于任意x∈E, 设f(x)=t2, 则x∈ft2⊆〈ft2〉. 从而有g(x)≥t2=f(x).

(3)若f⊆h且h是E的一个模糊滤子, 则g⊆h. 事实上, 对于任意x∈E,t∈[0,1],若x∈〈ft〉, 则存在ft中有限个元素a1,a2,…,an, 使得a1⊗…⊗an≤x, 对于任意i,1≤i≤n,因f(ai)≥t, 故h(ai)≥t,即ai∈ht, 又ht为E的滤子, 故a1⊗…⊗an∈ht,即h(x)≥h(a1⊗…⊗an)≥t. 从而有h(x)≥sup{t|t∈[0,1]且x∈〈ft〉}=g(x).

综上所述,g是包含f的最小模糊滤子, 即

〈f〉(x)=g(x)=sup{t|t∈[0,1]且x∈〈ft〉},

定义3 设f是E的一个模糊滤子, 若f(1)=1, 则称E的模糊滤子f是正规的.

NF(E)表示E的所有正规模糊滤子之集.

推论1NF(E)是F(E)的一个子格.

定理2 令

φ：NF(E)→FI(E),

fφ(f)={x∈E|f(x)=1},

则φ是态射且为一格同态.

证明 易知φ(1)=1. 对任意x,y∈E,有φ(x⊕y)=(f⊕g)(x)=f(x)+g(x)=2,φ(f)⊕φ(g)=f(x)+g(x)=2,即φ(f⊕g)=φ(f)⊕φ(g)，所以φ是态射.

对于任意f,g∈NF(E),

(1)φ(f∧g)=φ(f∩g)

={x∈E|f(x)∧g(x)=1}

={x∈E|f(x)=1}∩{x∈E:g(x)=1}

φ(f)∧φ(g).

(2)φ(f∨g) =φ(〈f∪g〉)

={x∈E|〈f∪g〉(x)=1},

φ(f)∨φ(g) =〈φ(f)∪φ(g)〉

=〈{x∈E|f(x)∨g(x)=1}〉.

若x∈φ(f)∨φ(g),则存在E中有限个元素a1,a2,…,an使f(ai)∨g(ai)=1,1≤i≤n.ai⊗…⊗an≤x. 因〈f∪g〉(ai)=1,1≤i≤n且φ(f∨g)为一滤子, 故有ai⊗…⊗an∈φ(f∨g),从而x∈φ(f∨g).若x∈φ(f∨g)则

1=〈f∪g〉(x)=sup{t∈E|x∈〈(f∪g)t〉},

故对任意t∈[0,1],x∈〈(f∪g)t〉,从而存在(f∪g)t中有限个元素b1,…,bn使b1⊗…⊗bn≤x.

由t的任意性知x∈φ(f)∨φ(g),

故φ(f∨g)=φ(f)∨φ(g).

综上所述，φ为一格同态.

2 模糊滤子诱导的同余关系

引理1 设f是E的一个滤子,E上的二元关系～定义为:

∀x,y∈E,x～y当且仅当x′⊕y∈f且y′⊕x∈f，则～是E上的同余关系.

定义4 设E是一个效应代数,f是E的一个模糊滤子,α∈[0,1], 定义E上的一个二元运算fα为

fα={(x,y)|(x,y)∈E×E,f(x′⊕y)>α,

f(y′⊕x)>α}

定理3 设f是E的一个模糊滤子, 对于α∈[0,1],fα≠Ø当且仅当f(1)>α.

证明 必要性 若fα≠Ø,则存在(x,y)∈E×E, 使f(x′⊕y)>α, 由模糊滤子定义(F1)知，当x≥y时有

f(1)=f(x′⊕x)≥f(x′⊕y)>α.

充分性 若f(1)>α,则

∀x∈E,f(x′⊕x)=f(1)>α,

因此∀x∈E,(x,x)∈fα,故fα≠Ø.

推论2 设f是E的一个模糊滤子,α∈[0,1],如果fα≠Ø,那么fα是E上的一个自反关系.

证明 由定理3可得

∀x∈E,f(x′⊕x)=f(1)>α,所以(x,x)∈fα. 因此fα是E上的一个自反关系.

定理4 设f是E的一个模糊滤子,α∈[0,1], 若fα≠Ø, 则∀(x,y)∈fα,∀x,y,z∈E,x,y,z两两可加, 都有

f((x′⊕z)′⊕(y′⊕z))>α,

f((y′⊕z)′⊕(x′⊕z))>α,

f((z′⊕x)′⊕(z′⊕y))>α,

f((z′⊕y)′⊕(z′⊕x))>α.

证明 因为

f((y′⊕x)′⊕(x′⊕z)′⊕(y′⊕z))

=f(y⊕y′)=f(1)>α,

又由(x,y)∈fα知,f(y′⊕x)>α. 所以由这两个不等式及f是E的一个模糊滤子可得

f((x′⊕z)′⊕(y′⊕z))

≥f((y′⊕x)′⊕(x′⊕z)′⊕(y′⊕z))∧f(y′⊕x)

=min{f((y′⊕x)′⊕(x′⊕z)′⊕(y′⊕z)),f(y′⊕x)}>α

在上述证明过程中除(x,y)∈fα外交换x和y的位置即可证f((y′⊕z)′⊕(x′⊕z))>α.

类似地可以证明后两个不等式.

推论3 设f是E的一个模糊滤子,α∈[0,1], 若fα≠Ø, 则∀(x,y)∈fα,∀z∈E都有

(x′⊕z,y′⊕z)∈fα, (z′⊕x,z′⊕y)∈fα

证明 因为∀(x,y)∈fα,∀z∈E，有

f((x′⊕z)′⊕(y′⊕z))=f(x⊕y′)>α

f((z′⊕x)′⊕(z′⊕y))=f(x′⊕y)>α

所以

(x′⊕z,y′⊕z)∈fα, (z′⊕x,z′⊕y)∈fα.

定理5 设f是E的一个模糊滤子,∀α∈[0,1],若fα≠Ø,则fα是E上的等价关系.

证明 (1)自反性:由推论2可知.

(2)对称性:显然.

(3)传递性:设(x,y),(y,z)∈fα.下面证明(x,z)∈fα.

由(x,z)∈fα及定理4可得,

f((y′⊕z)′⊕(x′⊕z))>α.

又由于(y,z)∈fα,所以f(y′⊕z)>α.

因此

f(x′⊕z)

≥min{f((y′⊕z)′⊕(x′⊕z)),f(x′⊕y)}>α.

类似可证,f(z′⊕x)>α.因此(x,z)∈fα.

综上所述,fα是E上的等价关系.

定理6 设f是E的一个模糊滤子,∀α∈[0,1], 若fα≠Ø, 则fα是E上的同余关系.

证明 ∀(x1,y1),(x2,y2)∈fα,则由推论3可得

注1 设f是E的一个模糊滤子,α=f(1), 则由文献[5]中的定理2.1可知fα是E上的一个滤子. 此时将E上的二元关系fα定义为

fα={(x,y)|(x,y)∈E×E,x′⊕y∈fα,

y′⊕x∈fα}

={(x,y)|(x,y)∈E×E,f(x′⊕y)=α,

f=(y′⊕x)=α}

引理1说明, 当α=f(1)时, 上面定义的fα仍是E上的同余关系.

注2 设f是E的一个模糊滤子, 令Af={fα|α∈[0,f(1)]}, 由fα≠Ø可知Af不是空集. 由定理6和注1知Af中每一个成员都是E上的一个同余关系.(Af,⊆) 构成一个偏序集, 且是一个链, 其中⊆是二元关系的包含, 此偏序集诱导的格记为(Af,∧,∨).

推论4f0是(Af,⊆) 中的最大元,ff(1)是(Af,⊆)中的最小元.

定理7 设Γ⊆[0,f(1)] , 则

证明 ∀α∈Γ,α≥inf(Γ),所以∀α∈Γ,fα⊆finf(Γ),因此finf(Γ)是{fα|α∈Γ} 的上界.

要证明finf(Γ)是{fα|α∈Γ} 的最小上界, 只需证明对∀β∈[0,f(1)]，若fβ⊂finf(Γ), 则fβ不是{fα|α∈Γ} 的上界.

[1] Foulis D, Bennett M K. Effect algebras and unsharp quantum logics[J]. Foundations of Physics, 1994, 24: 1 331-1 352.

[2] Wu Jing. Ideals, filters, and supports in Pseudo effect algebras[J]. Inter national Journal of Theoretical Physics, 2004, 43:349-358.

[3] 徐 扬, 秦克云. 模糊格蕴涵代数[J]. 西南交通大学学报, 1995,30(2)：121-127.

[4] Li Hai yang, Li Sheng gang. Congruences and ideals in pseudoeffect algebras[J]. Soft Computer, 2008,(12):487-492.

[5] 刘东利, 王国俊. 效应代数中的模糊滤子[J]. 模糊系统与数学, 2009, 23(3): 6-16.