基于区域特征的改进IHS图像融合算法

黄 伟 ，冯 径 ，柳亚婷 ，朱 建

（1.解放军理工大学 气象学院，江苏 南京 211101；2.解放军理工大学 工程兵工程学院，江苏 南京 210007）

图像融合是指利用各种成像传感器获得不同图像，综合各图像的互补信息和冗余信息，产生一幅新的图像，以获得更为精确、可靠、全面的图像描述，从而提高图像的信息分析和提取能力，并更适合于人眼感知[1]。图像融合的处理通常分为像素级、特征级和决策级3个层次，目前大部分研究集中在像素级融合，比较典型的算法有IHS变换法、PCA变换和基于多分辨率分析的方法等。这些算法都是针对整个图像场景进行处理，没有考虑到图像不同区域的空间特征，而通常图像中某一局部区域内的各像素点之间具有较强的相关性，图像中的区域特征往往需要通过多个像素来表征和体现[2]，因此，基于区域特征的图像融合方法更加合理，对降噪和配准的鲁棒性更强。

本文在研究基于区域特征的融合准则的基础上，提出了一种基于区域特征的结合IHS变换和小波变换的图像融合算法，首先分别对多光谱图像和高分辨率全色图像进行IHS变换和直方图匹配[3]，然后对相应频率分量进行小波融合时引入区域特征准则，最后通过实验验证了该算法的有效性和优越性。

1 IHS变换和小波变换

传统的基于IHS变换的图像融合方法存在一定的局限性[4]，首先，该方法要求替换I分量的图像P与I分量之间具有较大的相关性，但在许多实际应用场合，这种要求并不能得到满足，如果二者的相关性很低，有可能带来很大的光谱扭曲现象，针对这个缺点，不直接用P代替I分量，而是根据区域特征原理，以某个特征作为选取标准对P和I分量进行比较，选择更能体现图像细节特征的分量来充当新的I分量。其次，该方法仅适合于参与融合的多光谱图像3个波段的处理，对于多于3个波段的数据融合，IHS变换则无能为力，因此可以采用小波变换等其他方法进行融合。

传统的小波变换融合方法是先对进行融合的两幅图像进行小波分解，将分解后的高分辨率图像的高频分量和多光谱图像的低频分量结合，然后对其进行小波逆变换得到融合后的图像[5]。所得的融合图像在保留大部分光谱信息的同时，空间分辨率也有了一定的提高，但仍然存在一点的缺陷，例如，融合中舍弃了高分辨率图像的低频分量，虽然图中各区域的边界得到了较明显的增强，但图中平滑区域内部的灰度范围被压缩，图像比较昏暗，而且舍弃的低频分量中还含有一部分细节信息，使得融合效果不理想。

2 融合规则

为了克服IHS融合方法中光谱失真和小波变换融合方法图像会出现细节失真的缺点，本文采用结合IHS变换和小波变换的方法来融合多光谱图像和高分辨率图像，并在融合过程中分别对两幅图像小波分解后的低频分量和高频分量引入相应的区域特征准则，具体的融合过程如下：

1）将多光谱图像从RGB空间转换到IHS空间，得到I、H、S 3个分量；

2）高分辨率图像以亮度分量I为参考进行直方图匹配，得到的图像记为P，使之与多光谱图像保持较高的相关性；

3）对I分量和图像P分别进行n级小波分解，得到两组不同分解级上的各个频率的子图像；

4）对小波分解后的各频率子图像引入区域特征准则；

低频部分采用加权平均算子融合法，

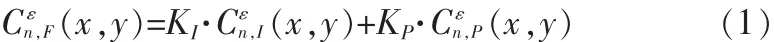
式中，I为多光谱图像经IHS变换后得到的亮度分量，P为高分辨率图像经过直方图匹配后得到的图像，F为融合后的图像，KI、KP为权系数，且 KI＞KP。

高频部分采用改进的区域方差加权融合法，首先选取以当前像素为中心的一个3×3局部区域，然后求出I分量和图像P的各分解层n、各方向ε上对应像素的区域方差，分别记为，再进行归一化处理。

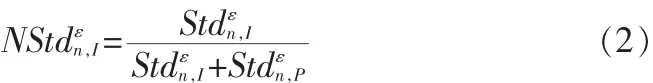
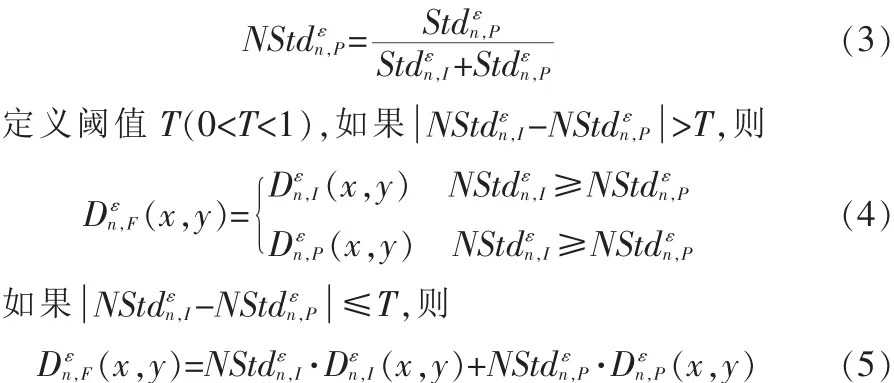
由以上规则可知，在对应的分解层和方向上，当I分量和图像P归一化后的区域方差值差别较大时 （Stdnε，I－Stdnε

，P），说明一幅图像的细节信息较丰富，而另一幅的细节信息则较少，此时选择区域方差较大的像素值作为融合后的小波系数，而当I分量和图像P归一化后的区域方差比较接近时，说明两者都含有丰富的细节信息，此时采用加权平均融合算子来确定融合后的小波系数。这样既可以保留图像的细节特征，又减少了噪声，保证了图像的融合效果。

5）以融合后的低频和高频小波系数进行小波逆变换，得到新的亮度分量I′。

6）用 I′代替步骤 1）得到的 I，并同 H、S分量图像经 IHS逆变换转RGB空间，得到融合后的图像。

文中算法的主要融合过程如图1所示。

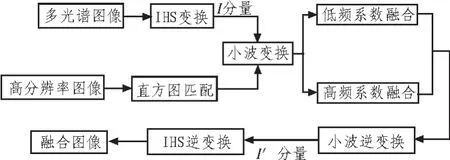
图1 本文算法的过程示意图Fig.1 The process schematic diagram of this algorithm

3 实验及结果分析

对于融合图像质量的评价通常采用主观判断和客观定量分析相结合的方法，本文采用的客观质量评价参数包括信息熵、均方根误差和平均梯度。信息熵是衡量图像信息丰富程度的一个重要指标，融合图像的熵越大，说明融合图像的信息量增加得越多；均方根误差用来衡量融合图像和标准参考图像，均方根误差越小，说明融合图像与理想图像越接近，融合效果和质量越好；平均梯度反映了图像中的微小细节反差与纹理变化特征，图像的平均梯度越大，表示图像的清晰度越好[6]。

文中选用的融合源图像为256×256的低分辨率多光谱图像和高分辨率全色图像，已经过配准，分别如图2（a）、图2（b）所示，理想图像如图2（c）所示。实验在matlab7仿真环境下进行，为了对比不同算法的图像融合效果，分别列出了IHS变换融合法、小波变换融合法和本文算法的融合结果图，分别如图 2（d）、图 2（e）和图 2（f）所示，小波分解级数均为 3 级。

从实验结果可以看出，图2（d）具有较好的清晰度，但图像色调偏暗，且明暗区域对比不是很明显；图2（e）的亮度较源图像有所增强，但是色彩不够丰富，且边缘细节较模糊；图2（f）的色彩和清晰度是3种融合结果中最佳的，亮度上有所提高，消除了传统IHS融合法对图像色调的影响，并且图像的边缘细节更加明显，清晰度提高。

3种算法的图像融合结果的客观评价参数如表1所示，可以看出，信息熵、均方根误差和平均梯度都从客观上说明了本文提出的算法要优于其他两种融合方法。

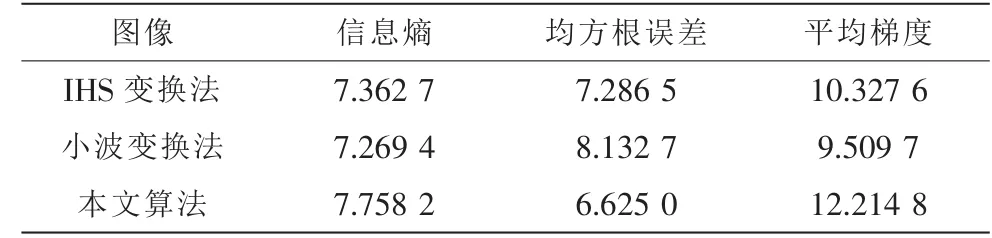
表1 3种融合方法的客观评价参数Tab.1 Objective evaluation parameters of three methods

4 结 论

文中提出了一种基于区域特征的结合IHS变换和小波变换的图像融合算法，首先分别对多光谱图像和高分辨率全色图像进行IHS变换和直方图匹配，然后对源图像小波分解后的相应频率分量进行融合时引入区域特征准则，克服了IHS融合方法中光谱失真和小波变换融合方法中图像会出现细节失真的缺点。实验结果表明，本文算法的融合图像色调明显，对比度强，清晰度高，比传统的IHS变换法和小波变换法更具优越性。

[1]郭雷，李晖晖，鲍永生.图像融合[M].北京:电子工业出版社，2008.

[2]李晖晖.基于区域分割的遥感图像融合方法[J].光子学报，2005，34（12）：1901-1905.LI Hui-hui. A region-based remote sensing image fusion method[J]. Acta Photonica Sinica，2005，34（12）:1901-1905.

[3]吴艳，杨万海，李明.多光谱与高分辨率图像融合算法研究[J].光子学报，2003，32（2）：174-178.WU Yan，YANG Wan-hai，LI Ming.Fusion algorithm of multispectral and high-resolution panchromatic images[J].Acta Photonica Sinica，2003，32（2）：174-178.

[4]Tu T M，Su S C，Shyu H C，et al.A new look at IHS-like imagefusion methods[J].Information Fusion，2001，2:177-186.

[5]Huang X S，Chen Z.A wavelet-based scene image fusion algorithm[C].Proceedings of IEEE TENCON，2002:602-605.

[6]兴旺，田秀华.基于边缘分割的多光谱图像融合方法[J].微计算机信息，2010，26（5）:204-205.XINGWang，TIANXiu-hua.Multispectral image fusion method based on edge segmentation[J].Control and Automation Publication Group，2010，26（5）:204-205.