在GPU上实现Jacobi迭代法的分析与设计
吴玫华
(福建省凯特科技有限公司 福建 福州 350002)
随着 GPU(Graphic Processing Unit,图形处理器)技术的快速发展,GPU的浮点运算能力迅速提升,并大幅度超过了通用CPU(Central Processing Unit)。早期GPU主要用于图形处理,硬件设计上主要考虑数据的并行,一般拥用大量的计算单元,而缺少CPU中用于分支预测、乱序执行等机制的逻辑控制单元,因此可利用GPU上的大量计算单元提升计算性能。Nvidia公司在2008年推出的GeForce GTX 280显卡的浮点计算峰值达到950Gflop/s,相对于当前主流多核CPU的性能提升了许多[1]。GPU的强大计算性能使得大批研究者投入到将大量计算需要和复杂的问题映射成GPU可处理的问题,即利用GPU来做的通用计算GPGPU(General Purpose Computation on GPU)[2]。
Jacobi迭代法[3]是科学计算领域中常用的计算方法,其核心计算是矩阵乘向量。Jacobi迭代法广泛用于求解线性方程组,是许多数值计算问题的核心,用于构成更高级的计算方法。研究这个经典算法在GPU上的实现对在GPU平台上开发相关科学计算程序具有重要的借鉴意义。
笔者在一个含有 Intel Core(TM)Duo E7200 CPU和Nvidia GeForce 9500GT GPU的计算机上实现Jacobi迭代法,并对算法性能进行测试。实验结果表明把算法映射到GPU上执行能够获得较好的加速比,最高得到10.2的加速比。
1 GPU通用计算
最早的GPGPU直接使用了图形学 API(Application Program Interface)编程。这种开发方式要求编程人员将数据打包成纹理,将计算任务映射为对纹理的渲染过程,用汇编或者高级着色语言(如 GLSL、Cg、HLSL)编写 Shader程序,然后通过图形学 API(如 Direct3D、OpenGL)执行。这种方式要求编程人员不仅要熟悉自己需要实现的计算和并行算法,还要对图形学硬件和编程接口有深入的了解。由于开发难度大,传统的GPGPU没有被广泛地应用[4-8]。
尽管在这期间许多非视觉的科学计算问题被成功地映射到显卡上[9-10],但是Nvidia公司发布的CUDA和开放运算语言OpenCL[11]框架才真正引领高性能计算进入了通用GPU计算时代。Nvidia公司于2007年正式发布的CUDA,是一种将GPU作为数据并行计算设备的软硬件体系。
Nvidia的CUDA架构通过对硬件的重新组织,使GPU能够应用于更一般的领域。CUDA试图通过提供一般的高层和低层的API来访问GPU的并行元素,以减轻将问题映射到GPU上的不便[12]。现在的GPU特别适合计算密集型、高度并行化的高性能计算[13]。CUDA提供了对显卡的抽象,把显卡作为能够同时执行大量轻量级线程的设备。这些线程组织成块,块中的每个线程能够访问它们自身的寄存器和块的共享存储器,每个线程也能够与其相邻的线程进行同步。一个内核函数的代码由一个或多个这样的块执行。由于具有CUDA能力的设备允许DRAM的类属存取(聚集和分散),所以每个线程都能访问GPU板卡上的显存和纹理存储器。
2 Jacobi迭代的实现
Jacobi迭代是用于求n元一次方程组ax=b的解。其中a为系数矩阵,x为解向量,b为常数向量。
Jacobi迭代的数学表示为:
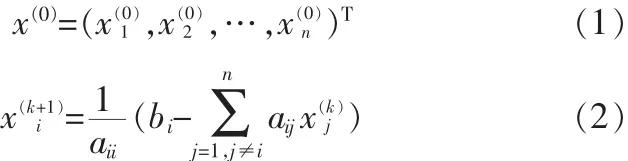
式(1)为给定的初始解向量,式(2)为第k+1次迭代中第i个元素的公式。当前后两次解向量的相对误差小于某个精度或迭代到一定次数,则认为算法结束,退出迭代,输出结果。可以发现式(2)中包含了矩阵乘向量以及向量的四则运算,这些都是可以并行的。
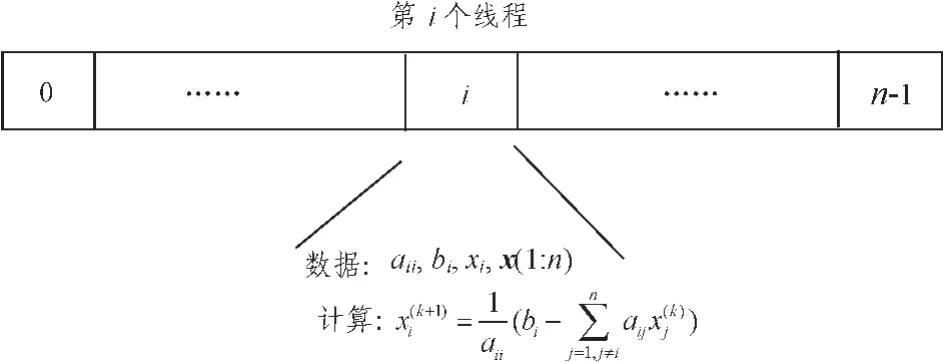
图1 Jacobi迭代的实现过程Fig.1 Basically implement of Jacobi
根据CUDA的编程模型,把每次解向量的计算放到GPU中运行,即kernel函数中实现。每个线程计算解向量的一个元素,因此可以得出每个线程上的数据和计算,如图1所示。映射到第i个线程的数据包括:矩阵a对角线的第i个元素aii;常数向量b的第i个元素bi;第k次迭代的解向量x中第i个元素xki。这3个数据与线程是一一对应的,即第i个线程只访问对应数据序列中的第i个元素。此外,在计算向量点积中还应包含矩阵a第i行的所有元素以及第k次迭代的整个x列向量。
1)基本算法
x_per=x_now= (0, …, 0); //设置初始解向量,x_per为前一次的解向量;x_now为当前解向量//
do
{
count++;//统计迭代次数//
Jacobi_kernel<<<grid, thread>>>( a, b, x_per, x_now );//调用GPU内核函数处理,每个内核函数处理一个解向量中的一个元素//
CopyDataDeviceToHost(x_per,x_now ); //将 GPU 中的数据复制回内存//
if(distance(x_per,x_now )<eps||count>MaxSteps)
Break;//两次的近似相对误差足够小或达到迭代次数上限则退出循环//
}while(ture).
以上为Jacobi迭代的基本实现方法。注意到GPU处理浮点数的速度较快,但GPU与CPU之间的数据传输会消耗大量时间。因此对基本实现方法进行一些修改,不用每次迭代后就将数据传输到CPU进行相对误差和迭代次数的判断,可以执行若干次迭代后再将数据传输回CPU进行判断,这样减少传输时间,从而提高执行效率。在理想情况下,在存储器传输进行的同时,GPU中的各线程也在计算。
2)改进算法
x_per=x_now= (0, …, 0); //设置初始解向量,x_per为前一次的解向量;x_now为当前解向量//
do{
count++;//统计迭代次数//
Jacobi_kernel<<<grid, thread>>>( a, b, x_per, x_now );//调用GPU内核函数处理,每个内核函数处理一个解向量中的一个元素//
if(count%10==0) //每执行10次迭代后进行判断//{
CopyDataDeviceToHost( x_per, x_now ); //将 GPU 中的数据复制回内存//
if(distance(x_per,x_now )<eps||count>MaxSteps)
Break;//两次的近似相对误差足够小或达到迭代次数上限则退出循环//
}
}while(ture).
3 实验结果
在 Intel Core2DuoE7200CPU(2core@2.53GHz)的 OpenMP 2.0计算平台和 NVIDIA GeForce 9500GT GPU (650 MHz)的CUDA SDK 2.0计算平台上分别测试由算法改写的程序在GPU上的运行情况和原始程序在CPU上的运行情况,其中CPU上的程序采用C++语言编写,并使用OpenMP在双核上并行执行。
在不同矩阵规模下测试了在GPU下的两种实现策略与双核CPU程序的性能,结果如图2所示。
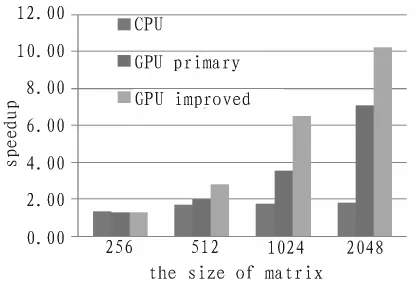
图2 实验结果性能对比Fig.2 Speedup of algorithms
图2 分别给出了Jacobi迭代在各种规模下双核CPU程序、GPU基本实现、GPU改进实现的性能对比。从图中可以看出,GPU程序加速比随着数据规模的增大而增大。GPU处理单元的频率(650 MHz)远小于 CPU(2.53 GHz)的频率。 GPU的性能优势来自于众多的计算单元,以庞大的吞吐率同时进行多点计算,因此要保证GPU性能的发挥,必须提供足够多的可以并行的计算量。从图2中还可以看出,在矩阵规模为256×256时,GPU的性能低于双核CPU程序。一方面是因为计算量较小,无法发挥GPU的性能,另一方面是因为调用kernel函数也存在一定开销,如果计算量太小则计算的开销无法抵消这部分调用的开销。
4 结束语
将数值计算有效地映射到GPU上执行必须考虑多方面的因素,包括访问的效率、分支语句的处理等。本文将科学计算领域中常用的Jacobi迭代在GPU上实现,对数据访问进行优化,获得了良好的加速比。从实验结果也可以看出,随着矩阵规模的增大GPU程序的加速比也在增大,说明算法的可扩展性良好。
[1]NVIDIA.NVIDIA CUDA programming guid version 2.0[S].2008.
[2]JD Owens,M Houston,D Luebke, et al.GPU Computing[J].Proceedings of the IEEE,2008,96(5):879-899.
[3]Jeffery JL.Numerical Analysis and Scientific Computation[M].Addison Wesley,2004.
[4]Kessenich J, Baldwin D, Rost R.The OpenCL Shading Language[R].2003.
[5]Mark W R,Glanville R S,Akeley K,et al.Cg:A system for programming graphics hardware in a clike language[J].ACM Transactions on Graphics-Proceedings of ACM SIGGRAPH,2003,22(3):897-907.
[6]Microsoft.High2Level Shader Language[S].2003.
[7]Pike A.DirectX 8 Tutorial[R].Retrieved March 15,2006.
[8]Shreiner D,Woo M,Neider J,etal.OpenGLProgramming Manual[M].OpenGL ARB, Boston.5th ed.Addison Wes2ley,2005.
[9]Svetlin A M.CUDA compatible GPU as an efficient hard-ware accelerator for AEScryptography[C]//In Proceedings of IEEE International Conference on Signal Processing and Communication,2007:65-68.
[10]Szerwinski R,Guneysu T.Exploiting the power of GPUs for Asymmetric Cryptography[J].Lecture Notes in Computer Science,2008:79-99.
[11]KHRONOS:OpenCL overview web page[EB/OL]. (2009)http://www.khronos.org/opencl/,2009.
[12]Halfhill T.Parallel Processing with CUDA[M].Microprocessor,2008.
[13]Gummaraju J,Rosenblum M. Stream processing in generalpur-pose processors[S].2005.

