基于时滞惯性流形的二维平面壁板非线性气动弹性分析

梅冠华，张家忠，席 光

（西安交通大学 能源与动力工程学院，西安 710049）

气动弹性领域主要研究气动力和弹性结构变形之间的相互作用。气动力产生结构变形，而结构变形又影响着气动力，这种气动力和变形间的耦合作用导致了流体和固体复杂的动力学响应。如颤振、混沌等。这些响应的深入分析对于揭示流固耦合问题的本质，对于该类非线性振动的避免、控制和利用都具有十分重要的意义［1］。

气动弹性问题中的非线性来源于气动力和结构体两方面：流场中的激波、分离会导致结构变形与气动力的非线性关系；几何大变形、材料非线性会引起结构体受力与其变形的非线性关系［2-4］。理论上为准确描述这种非线性气动弹性问题，需综合考虑气动力和结构体的非线性效应。对于目前的气动弹性分析，一部分考虑了气动力的非线性，结构体采用线性假设；一部分考虑了结构体的非线性，气动力采用线性假设；综合考虑两方面非线性特性的分析较为少见。

作为典型的非线性气动弹性问题，对于二维平面壁板颤振模型，平板变形采用Von Karman几何大变形理论，气动力采用修正一阶活塞理论近似，推导出系统的非线性偏微分控制方程。Dowell［5］运用传统Galerkin方法（TGM）研究了系统不同控制参数对于颤振边界和振动幅值的影响，并与实验结果进行对比。然而模态数目的选取是TGM中的关键问题，若选取过少则不能获得精确解，若选取过多则耗费大量计算时间。惯性流形的提出简化了系统离散方程的维数，在保证计算精度的同时减少了计算量。惯性流形（IM）、近似惯性流形（AIM）和时滞惯性流形（IMD）的概念反映了非线性发展方程的高阶模态与低阶模态间的相互作用规律［6-8］。IMD提出非线性发展方程的高阶模态不仅依赖于当前低阶模态分量值，还依赖于高阶分量某个时间间隔以前的值［9-10］。IMD较AIM更加符合实际情况，不仅存在条件大为宽松，且具有良好的收敛性和稳定性［11］。基于IMD思想的非线性Galerkin方法被引入到二维平面壁板颤振模型的求解中，与TGM结果对比发现精度不变且节省计算时间和资源。

对计算结果，分别以无量纲动压和无量纲压缩内力为分岔参数，无量纲振幅为响应作出分岔图形，发现阵发性通向混沌的途径，混沌区域表现出周期窗口和自相似特性。通过对系统的相图、位移的FFT频谱以及Lyapunov指数的分析，验证系统存在稳定、屈曲、谐调和非谐调运动四种典型类型。对非谐调运动的详细研究发现系统存在倍周期运动、准周期运动和混沌运动等丰富的非线性响应。研究结果为识别和进一步控制此类非线性现象提供了依据。

1 力学模型

二维平面壁板颤振模型如图1所示：平板长度为a，为方便理论分析，假设宽度b→∞，则问题简化成二维平板，两端初始拉伸内力N0，平板厚度为h，单位长度质量为ρ，弹性模量E，泊松比μ，上表面沿x方向来流速度为U∞，马赫数M∞≫1，空气密度ρ∞，边界条件为两端简支。

在Kirchhoff-Love假设下，仅考虑板的横向振动w（x，t），应变位移关系采用Von Karman几何非线性大变形理论表示，给出平板运动方程［5］：

图1 二维平面壁板颤振模型Fig.1 2-Dimensional panel flutter model

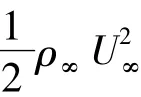
引入无量纲参数：

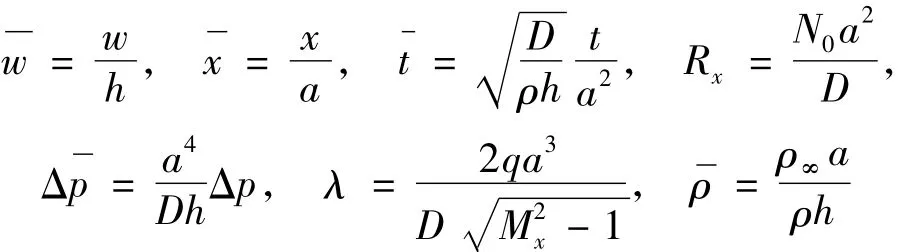
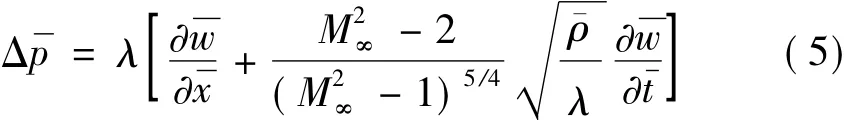
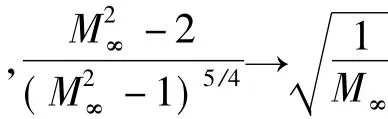
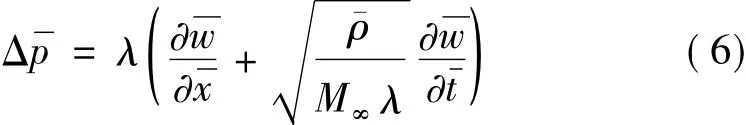
系统控制方程（1）无量纲化为：

边界条件（4）无量纲化为：

2 数值求解方法

根据传统Galerkin方法，构造满足边界条件（8）的基函数列：sin（iπ），i=1，2，…。平板的位移可以设为此函数列的叠加形式：

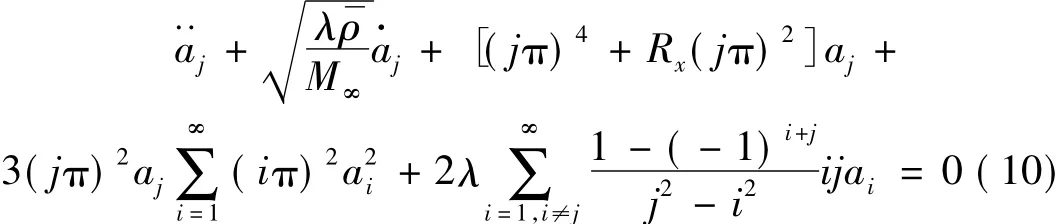
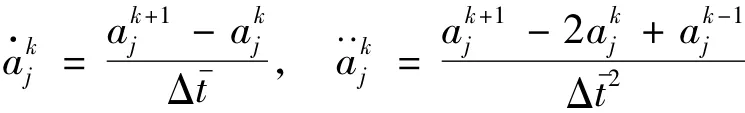
得到k时刻后N个高阶模态方程组为：

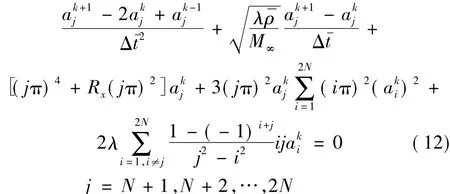
此代数方程组实现了后N个高阶模态用前N个低阶模态表示，且加入了时间滞后。这样后N个高阶模态不用通过繁琐的数值积分，而是直接求解代数方程组得到，从而节省了计算时间。

3 数值分析

为了获得系统的精确解至少需要4到6阶模态，对于4阶以上模态系统的理论分析较为困难，多以数值模拟为主。系统的三个控制参数/M∞、无量纲拉伸内力Rx和无量纲动压λ中∞影响微小，Rx和λ影响显著。由于压缩内力是系统趋于不稳定的因素，因为方便分析，定义无量纲压缩内力R=-Rx/π2，注意R与Rx的方向相反。取定∞=0.01，分别选取λ和R作为分岔参数，采用6阶模态进行数值计算，以=0.75为参考点，计算时间充分长以消除瞬态响应，系统达到稳态响应后，若为平面稳定或屈曲则取其无量纲变形，若为振动则取其无量纲速度=0时刻的无量纲振幅，即取相图上=0直线与系统轨道交点处的值，以此为响应绘制系统分岔图。对于特定参数下系统响应，采用图相图、稳态的FFT频谱图以及Lyapunov指数综合分析。

频谱图中横坐标为无量纲频率，纵坐标为幅值，其反映系统所含不同频率正弦振动分量所占比重，直观上若频谱图中仅有单个脉冲的峰值，则仅含单独频率分量，为谐调运动；若频谱图中存在有限个脉冲峰值，则为有限个频率下正弦振动的叠加，若频率间呈倍数关系，即存在公约数，则为倍周期运动，若频率间不存在倍数关系，即频率成分不可互约，则为准周期运动；若存在无穷个峰值密布于频谱图上，则此状态为混沌，在相图上表现为有限区域内杂乱的非封闭曲线。

混沌的更精确代数判定可用Lyapunov指数［14］，其反应系统初始微小偏差随时间趋于无穷的指数膨胀或收缩状况，正值表示膨胀，零值表示周期运动，负值表示收缩，其绝对值大小表示收缩或膨胀程度的强弱。一般而言系统最大Lyapunov指数为正值则可认为达到混沌状态。采用经典单位球演化伴随GSR正交化置换新矢量的算法计算六阶模态下系统全部Lyapunov指数，若出现正值则认为达到混沌状态，不同参数下混沌系统的前三个Lyapunov指数如表1所示。

表1 不同参数下混沌系统的前三个Lyapunov指数Tab.1 First three Lyapunov Exponents of chaos systems at different parameters

3.1 TGM与IMD计算结果的比较

R=0即平板两端不受初始内力的状况下，当无量纲动压λ逐渐增大跨过临界值λcr=345后，平板发生Hopf分岔，由静态稳定转化为极限环振动，且振幅随λ的增大而增大，如图2（a）所示。FFT频谱分析表明系统仅含单独频率，且该频率随着λ的增大而增大，如图2（b）所示。与TGM结果对比发现IMD结果保留原有精度。

图 2 R=0，振幅和频率随λ变化图Fig.2 Amplitude and frequencyvs.λ at R=0

λ=0即无气动载荷状况下，随R的变化如图3所示。当R逐渐增大跨过临界值Rcr时，平板由静态稳定转化为屈曲失稳，到达两个变形位置中的一个。且变形量随R增大而增大。对比发现IMD结果与TGM结果吻合较好。

3.2 λ变化对系统响应的影响

固定无量纲压缩内力R=4，考虑无量纲动压λ变化对系统响应的影响。以λ为分岔参数，为响应的分岔图如图4所示。

当0＜λ＜114时，系统表现为屈曲，到达两个变形位置中的一个，以λ=100为例如图5（a）所示；

当114＜λ＜159时，系统演变为混沌，以λ=120为例如图5（b）所示，前两个Lyapunov指数为正值如表1所示；

当159＜λ＜173时，系统表现为倍周期运动。以λ=160为例如图5（c）所示，首频率1.59 Hz占据主要地位，各频率间呈现 1、2、3、4、5 倍频关系，2 倍和 5 倍频贡献十分微小，如表2所示；

当173＜λ＜227时，系统演化为混沌状态，以λ=210为例如图5（d）所示，其前两个Lyapunov指数为正值如表1所示；

当227＜λ＜249时，系统发生倒分岔最终演化为单周期振动，以λ=260为例如图5（e）所示，首频率占据了绝对统治地位如表2所示。

图3 λ =0，屈曲变形随R变化图Fig.3 Buckling deformation vs.R at λ =0

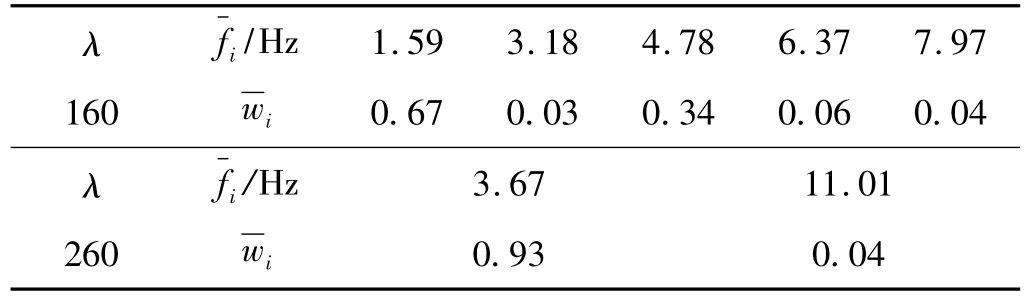
表2 R=4，不同λ下系统主要频率分量及其幅值Tab.2 Main frequencies and their amplitudes of different λ at R=4

图4 R=4，随λ的分岔图Fig.4 Bifurcation diagram of with λ at R=4

3.3 R变化对系统响应的影响

固定无量纲动压λ=200，考虑无量纲压缩内力R变化对系统响应的影响。以R为分岔参数，w为响应绘制分岔图如图6所示，其中图6（a）为整体图，图6（b）为局部放大图。

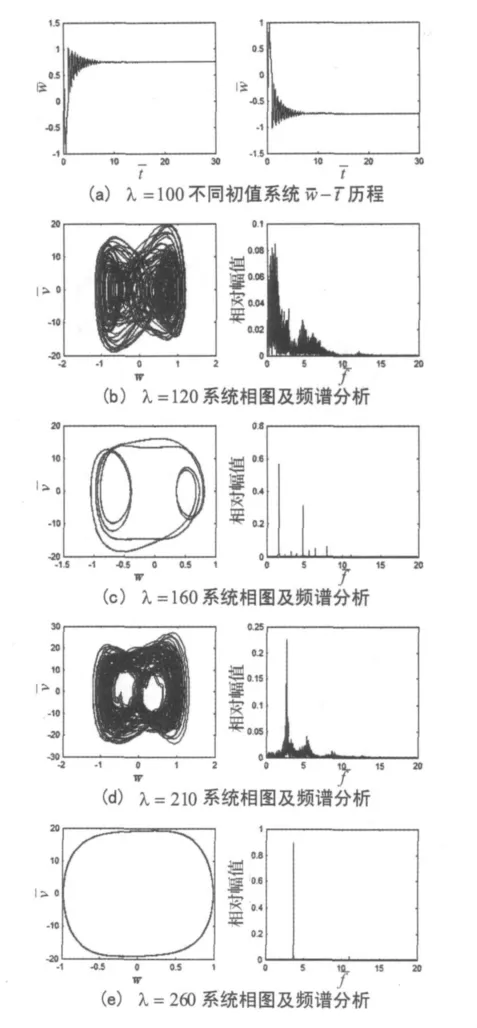
图5 R=4，不同λ下系统相图及频谱分析Fig.5 System phase portraits and spectra analysis of different λ at R=4

当0≤R≤1.875时，系统表现为平面稳定，以R=1.0为例如图7（a）所示，对于任何初始扰动，系统最终回复到静态平衡位置；

当1.876≤R≤3.325 时，系统发生 Hopf分岔，表现为谐调振动，以R=2.5为例如图7（b）所示，振动仅含单独频率3.29 Hz；

当3.326≤R≤3.623时，系统发生一系列倍周期-准周期间歇型的分岔，即为阵发性途径最终通向混沌：以R=3.5，R=3.55为代表的倍周期运动如图7（c）～图7（d）所示，其各频率成分间呈现出倍数关系如表3 所示；以R=3.43，R=3.54 和R=3.60 为代表的准周期运动如图7（e）～图7（g）所示，其各频率成份间并不存在倍数关系，如表3所示。这是由于系统的非线性特性，不同频率的模态间存在耦合，导致在特定状态下单独模态或多个模态占据主导地位，系统则表现为单频率或是多个频率组合的振动形式，故而出现如上复杂的振动行为。

当3.624≤R≤5时，系统通过上述间歇型分岔最终进混沌状态，混沌图形中的自相似结构以及周期亮窗等特性呈现在分岔局部放大图6（b）中。以R=4.5为例的混沌运动如图7（h）所示，其前两个Lyapunov指数均大于零如表1所示。

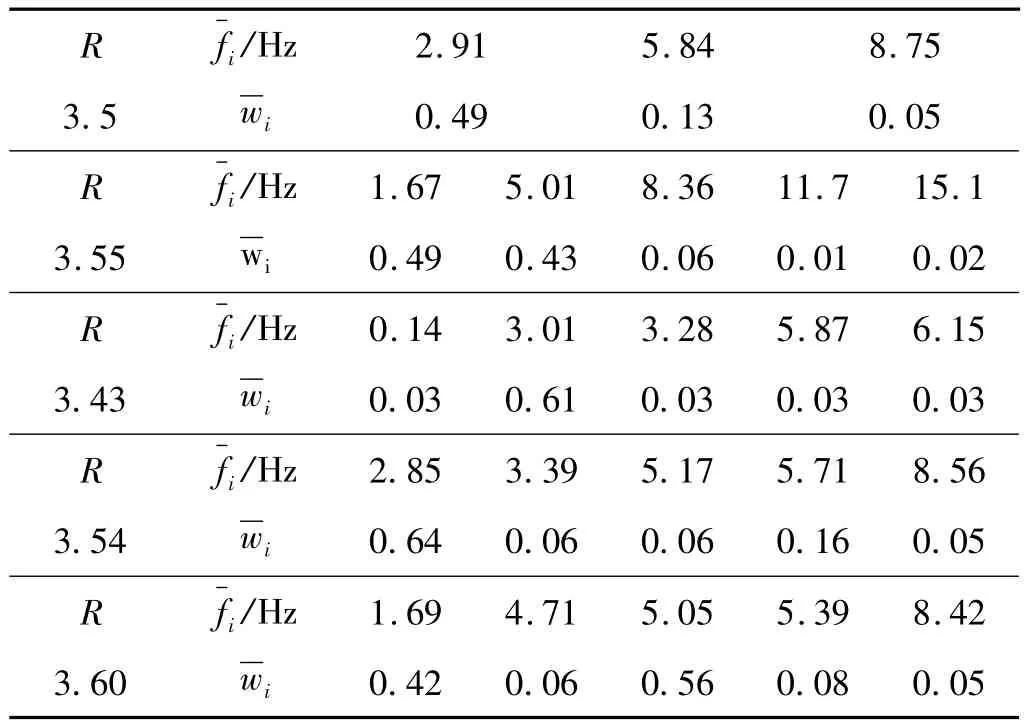
表3 λ=200不同R下系统主要频率分量及其幅值Tab.3 Main frequencies and their amplitudes of different R at λ=200

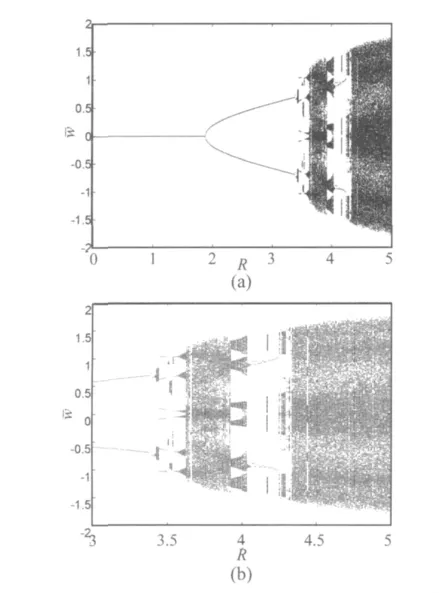
图6 λ=200，随R分岔图Fig.6 Bifurcation diagram of with R at λ=200

4 结论

（1）将基于IMD的非线性Galerkin方法引入到二维平面壁板颤振模型的求解中，结果表明IMD在保留了TGM精度的同时，可以缩减求解维数，大量节省计算时间，为IMD求解类似问题提供了借鉴。

（2）系统的两个主要参数，即λ和R将响应分为多个区域，即：二维平面壁板气动弹性系统在不同参数下表现出平面稳定、屈曲变形失稳、谐调振动、倍周期振动、准周期振动以及混沌等丰富的非线性现象。

（3）分别以λ和R为分岔参数，为响应得出系统分岔图形，通过对其分析发现存在阵发性通向混沌的途径，观察到混沌中的自相似结构以及周期窗口现象。

（4）Lyapunov指数是精确判断混沌的代数判据，出现正值时即可认定系统处于混沌状态，FFT所得频谱图反映了系统所含频率分量及其所占比重，可以定性地识别系统响应。

（5）本文所采用的方法可以用于指导该类非线性气动弹性问题机理的进一步深入研究，所得出的结论可对该类现象的识别和控制提供依据。进而合理利用自激振动现象实现延迟激波产生、延迟分离点和增升减阻等效果。

［1］Kang W，Zhang J Z，Feng P H.Numerical simulation and Aeroelastic Analysis of a Local Flexible Airfoil at Low Reynolds Numbers［A］.In：The 8th Asian Computational Fluid Dynamics Conference［C］.Hong Kong，China，2010：10-14.

［2］Dowell E H. Some recent advances in nonlinear aeroelasticity：fluid-structure interaction in the 21st century［A］.In：51st AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，and Materials Conference，18th AIAA/ASME/AHS Adaptive Structures Conference［C］//Orlando，Florida，USA，2010：12-15.

［3］Dowell E H，Edwards J，Strganac T.Nonlinear aeroelasticity［J］.Journal of Aircraft，2003，40（5）：857-874.

［4］Dowell E H，Tang D.Nonlinear aeroelasticity and unsteady aerodynamics［J］.AIAA Journal，2002，40（9）：1697-1707.

［5］ Dowell E H.Nonlinear oscillations of a fluttering plate I［J］.AIAA Journal，1966，4（7）：1267-1275.

［6］ Zhang J Z，Liu Y，Lei P F，et al.Dynamic snap-through buckling analysis of shallow arches under impact load based on approximate inertialmanifolds［J］. Dynamics of Continuous， Discreteand ImpulsiveSystems， SeriesB（DCDIS-B），2007，14（S5）：287-291.

［7］Foias C， SellG R. Inertialmanifolds fornonlinear evolutionary equations［J］.Journal of Differential Equations，1988，73（2）：309-353.

［8］ Foias C，Manley O，Temam R.On the interaction of small eddies in Ttwo-dimensional turbulence flows［J］.Math Modeling and Numerical Analysis，1988，M 2AN，22（1）：93-114.

［9］ Debussche A，Temam R.Inertial manifolds with delay［J］.Appl.Math.Lett，1995，8（2）：21-24.

［10］戴正德，郭柏灵.惯性流形与近似惯性流形［M］.北京：科学出版社，2000.

［11］张家忠，陈丽莺，梅冠华，等.基于时滞惯性流形的浅拱动力屈曲研究［J］.振动与冲击，2009，28（6）：100-103.

［12］Ashley H，Zartarian G.Piston theory-a new aerodynamic tool for the aaeroelastician［J］.Journal of the Aeronautical Science，1956，23（12）：1109-1118.

［13］ Zhang W W，Ye Z Y，Zhang C A，et al.Supersonic flutter analysis based on a local piston theory［J］.AIAA Journal，2009，47（10）：2321-2328.

［14］ Wolf A，Swift J B，Swinney H L，et al.Determining lyapunov exponents from a time series［J］.Physica D，1985，16（3）：285-317.