通过附加浮筒改良的张力腿平台多体耦合运动响应
闫功伟,欧进萍,2
(1.哈尔滨工业大学 土木工程学院,哈尔滨 150090;2.大连理工大学 建设工程学部,大连 116024)
张力腿平台(Tension Leg Platform,简称TLP),由甲板、立柱、浮筒、张力腿、立管和基础等几部分组成,是一种已经被广泛应用于世界深海油气工程中的半固定半顺应式平台。它通过平行且张紧的竖向张力腿系统与海底相连,保证了平台在纵、横摇和垂荡方向上的良好性能。而平台在纵、横荡和首摇方向上则具有顺应式平台的特征,以很大的惯性力来平衡外荷载,具有较小的运动响应。然而当环境条件更为恶劣或平台就位水深更深时,平台纵、横荡及垂荡方向的运动就很难再满足生产的要求,这在很大程度上限制了TLP在更深海域的应用。
国内外众多学者已经对TLP做了大量的研究,主要集中在TLP环境载荷及其耦合作用、平台形式创新和平台动力响应问题上。Donley等[1]对受到浪、流共同作用的TLP进行了随机响应分析。Vickery[2]从理论和实验两方面研究了风力和波浪对TLP的耦合作用。Kim等[3]指出张力腿和立管均会对深水TLP贡献刚度、阻尼及质量,因此数值模拟中使用包括张力腿、立管及主体的耦合系统是必要的。胡志敏等[4]对波浪载荷的辐射效应深入研究,并以附加质量、附加阻尼等水动力参数的形式计算了辐射效应对TLP的载荷影响。曾晓辉[5-6]等考虑了多种非线性因素对TLP动力响应的影响,推导了TLP六自由度非线性运动方程,并对平台在有限振幅和有限位移条件下的动力响应分别进行了研究。Taflanidis等[7]研究设计了一个质量阻尼器,用于减小平台的运动响应。Yang等[8]进行了位于墨西哥湾的延伸式TLP平台在极端海况下张力腿断开时瞬态效应的数值模拟。
本文提出了在传统式TLP平台张力腿上附加浮筒的新型优化方案,根据我国南海某海域实际海况,分别计算了平台受到的风、浪、流及其联合作用,对比分析了附加浮筒净浮力大小及其就位水深对平台整体运动响应的影响,并进一步模拟了在风、流和随机波浪共同作用下附加浮筒平台的多体耦合运动响应。
定性分析可知,附加浮筒提高了张力腿的内张力,增加了张力腿对平台上体的系泊作用,从而能够减小平台在各方向上的运动响应。附加浮筒自身的水动力性能将会影响到平台的运动响应,同时将系泊系统分成了上、下两个部分。这样还可以降低对平台上体与附加浮筒之间的系泊索的内张力要求,减小张力腿平台对上体荷载的敏感性,适应不同的海况和工作条件。
除了定性分析,本文还通过数值模拟实现了对平台上体、多个浮筒和上、下两段张力腿之间的多体耦合运动响应的分析。多体之间的耦合运动响应是数值模拟的重点和难点,需要根据各浮体和张力腿的运动方程和相互之间的协调条件进行复杂的迭代求解。
1 多体耦合运动分析模型
1.1 模型参数
本文的分析是作为一般方法考虑的,但具体数值计算将采用下面经过总体设计的传统式TLP平台及参数,如图1所示,平台关于x轴和y轴对称。下文给出平台上体、张力腿及附加浮筒的形式及参数。
表1给出了用于分析的传统式TLP平台上体的主要参数。表2中列出了张力腿的参数,包括张力腿的直径、壁厚、就位长度和组成。图1为TLP上体示意图。

图1 TLP主体Fig.1 Hull of TLP

表1 TLP主要参数Tab.1 TLP Parameters

表2 张力腿参数Tab.2 Tendon parameters
图2为平台张力腿上附加浮筒后的就位示意图。附加浮筒没入海平面以下较深处,连接上、下两端张力腿,具体的参数在下文与数值模拟考虑的工况一起给出。
1.2 时域下多体耦合迭代求解方法
分别建立张力腿平台上体、附加附体、上段张力腿和下段张力腿的运动方程,将各浮体的系泊力和张力腿的端部节点力单独列于方程右侧,两者是成对的作用与反作用力,以此为连接可以将各运动方程联立,在时域下通过迭代考虑各浮体和张立腿之间的耦合运动效应。
t时刻,前文提到的各个浮体和张力腿的运动方程均可以表示成如下形式:

图2 带有附加浮筒的TLPFig.2 TLP with additional pontoons

其中:M为各浮体和张力腿的总质量矩阵(包含由于运动而产生的附近质量矩阵);Fm为各浮体受到的系泊力或者各张力腿的端部节点力矢量;C为各浮体和张力腿运动的阻尼系数(包括流体粘滞阻尼系数和因运动产生的辐射阻尼系数);K为各浮体和张力腿单独运动的刚度矩阵;Fi为各浮体和张力腿受到的其他载荷作用矢量。(t),(t),X(t)分别为各浮体和张力腿运动的加速度、速度和位移矢量。方程中各变量单位均采用国际单位制。
各浮体与张力腿之间为刚接,还需满足受力、运动及变形协调的条件。
根据上述运动方程及协调条件建立迭代求解的格式,对于(t+dt)时刻:

则:

上述多体耦合运动的迭代求解格式,实际上是逐步逼近多体之间的受力及变形协调条件的过程。由于方程右侧各荷载的计算也与各体的位移和速度有关,浮体的系泊力与系泊索顶端张力这一对作用与反作用力与各体的变形与运动响应相关,因此,多体耦合的问题将是一个复杂的循环迭代求解过程。本文通过数值模拟的方法来实现多体的耦合运动的模拟及求解。
2 TLP所受环境载荷
TLP就位于深海环境当中,会受到风、浪、流及其联合作用,本文此节主要结合我国南海典型海况环境条件,分析在不同荷载作用下平台的运动响应。
2.1 环境条件
平台响应分析选用的海洋环境参数为本研究项目基础资料中给出的我国南海某海域百年以上海况条件,如表3所示,其中给出了该海域的平均风速、平均流速、有义波高、谱峰周期等参数。

表3 环境参数Tab.3 Environment parameters
选择风、浪、流的入射角均为零的最不利工况,根据平台整体设计结果,计算结构总的风力,可以得出平台上体总风力系数CW总=1.3E3 kg/m,计算平台上体所受总得流力,得出平台上体总流力系数CC总=4.330E5 kg/m。
3 模型水动力参数计算
以前文给定模型为研究对象,下文给出该模型的各水动力参数。
波浪力也可称为波浪激振力,与波浪运动有关,引起浮体的摇荡运动。根据绕射和辐射理论,浮体受到的波浪力可以分为入射波浪力(F-K力)、绕射波浪力和辐射波浪力[9]。
具体数值计算可采用AQWA-LINE软件模块对平台上体的自由浮体状态进行数值模拟。
3.1 平台上体水动力参数
3.1.1 F-K 力
佛劳得-克利洛夫力(Froude-Krylov force,简称F-K力)由未扰动波浪下的动态压力场引起。它和绕射力共同组成了在规则波下作用在浮体上的非粘性力。
在单位波幅波浪作用下给定平台上体受到的F-K力如图3所示。

图3 平台上体各方向F-K力Fig.3 F-K loads of TLP hull
3.1.2 绕射力
当浮体尺度与波浪相比较大时,入射波浪在遇到静止浮体时,在其表面产生一个向外散射的波浪,从而与入射波浪叠加形成新的波浪场,这种现象称之为浮体的绕射现象,而静止浮体受到绕射波浪场作的作用称之为绕射力。它实际上是对“弗劳德-克雷洛夫”假定的修正,当物体的尺寸相对于波长较小时(物体特征尺寸小于波长的20%),绕射力可忽略不计。本例中,单位波幅波浪作用下TLP上体受到的绕射力如图4所示。

图4 平台上体绕射力Fig.4 Diffraction loads of TLP hull
3.1.3 平均波浪漂移力
波浪漂移力表示的是波浪产生的持续的平均波浪阻抗,为二阶量。通常计算平均漂移力分远场解法和近场解法,前者可求得纵、横荡和首摇3个分量,而后者可求得全部6个分量[10]。本例中平台关于x、y轴对称,波浪0°入射,采用远程解法可以计算出平台在单位波幅波浪作用下的纵荡方向上的平均波浪漂移力,其取值如图5所示。
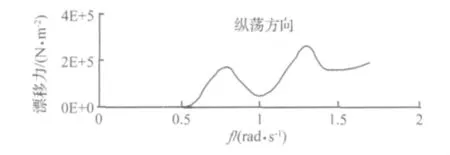
图5 平台上体平均波浪漂移力Fig.5 Mean drift force of TLP hull
3.1.4 辐射阻尼
辐射力是物体在由于自身运动而产生的辐射波浪场中所受到的阻力,可以用辐射阻尼来表征。平台辐射阻尼是一个6×6的矩阵。由于平台的对称性,R11=R22,R44=R55,R15=-R24,Rij=Rji。图 6 给出了平台上体辐射阻尼的取值,其他未列出来Rij均为零。

图6 平台上体辐射阻尼Fig.6 Radiation damping of TLP hull
3.1.5 附加质量
当浮体在水中加速运动时,会带动周围流体做加速运动,流体的惯性就会表现为对浮体的反作用力,这个力被称作浮体的附加质量力。
平台上体的附加质量也是一个6×6的矩阵,由于平台的对称性,M11=M22,M44=M55,M15=-M24,Mij=Mji,图7给出了平台上体附加质量的取值,其他未列出来的值为零。

图7 平台上体附加质量Fig.7 Added mass of TLP hull
3.2 单个附加浮筒的水动力参数
3.2.1 辐射阻尼
附加浮筒设置在海面较深处,且尺寸比平台主体小很多,其辐射阻尼远小于平台上体的辐射阻尼。因此整体计算中忽略了附加浮筒的辐射阻尼对平台运动响应影响。
3.2.2 附加质量
附加浮筒完全浸入水中,不随水深变化而变化。单个附加浮筒的附加质量由其尺寸决定,由模拟软件自动根据尺寸计算得出。
4 数值模拟及运动响应分析对比
4.1 数值模拟流程[11]
(1)建立平台上体及附加浮筒的水动力模型。
(2)计算平台上体及附加浮筒的水动力参数:RAOs,附加质量,附加阻尼,波浪荷载和平均波浪漂移力等信息。
(3)增加系泊系统,即张力腿系统,将平台上体和附加浮筒连接,并固定于海底,分析该耦合系统分别在风、浪、流载荷及其联合作用下的运动响应。
(4)对分析结果进行提取分析处理,给出结论。
4.2 平台的数值模拟工况
本文考虑荷载的最不利情况,假设风浪流载荷均沿0°角入射,则平台主要产生纵荡、垂荡和纵摇运动,主要分以下工况分析平台的运动响应:
(1)附加浮筒位置改变:以附加浮筒提供净浮力为平台0.6倍净浮力的参数为基准,分别考虑附加浮筒质心距静海面距离为:100 m,200 m,300 m,400 m,500 m时附加浮筒的水动力参数及平台运动响应的分析;
(2)附加浮筒浮力改变:以附加浮筒质心距海面100 m为基准,分别考虑附加浮筒净浮力为平台上体净浮力的1 倍、0.8 倍、0.6 倍、0.4 倍0.2 倍。
相应的附加浮筒尺寸如表4所示。

表4 附加浮筒参数确定Tab.4 Parameters of additional pontoon
浮筒的平均密度按经验可以取为180 kg/m3。根据以上参数可以计算出单个浮筒各方向上的转动惯量,在计算平台运动响应时需要用到。
4.3 不同环境荷载作用分析
考虑附加浮筒的不同水深及不同浮力大小,分别对风荷载、流荷载、规则波浪荷载及其联合作用下TLP平台的运动响应进行数值分析,将结果进行对比分析。
图8是平台在不同水深附加0.6倍净浮力浮筒时的运动响应分析结果,图9是平台在100 m水深附加不同浮力浮筒时的运动响应分析结果。表5是无附加浮筒时各荷载下平台运动响应极值及各荷载对平台运动响应的贡献比例分析。

图8 平台在不同水深附加浮筒时的运动响应分析Fig.8 Motion responses of TLP added pontoons in different depth
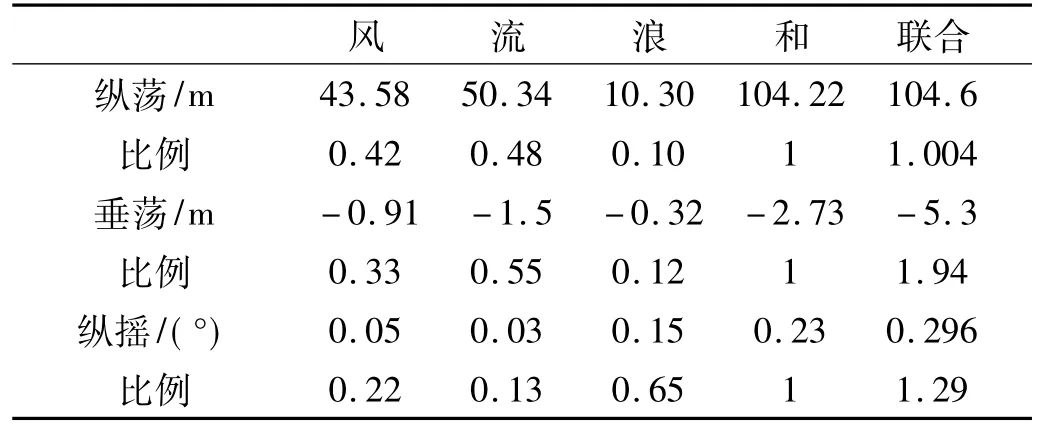
表5 各荷载作用下无附加浮筒TLP的极值响应分析Tab.5 Extreme response analysis of TLP with different loads
结合平台运动响应时程,由图8、9和表5可以看出:
(1)TLP平台有无附加浮筒时,均在入射角为0°的平均风、流荷载的作用下产生明显的纵荡和垂荡响应和较小的纵摇响应,风和流的作用效果接近。波浪使得平台在新的平衡位置发生在纵荡、垂荡和纵摇方向上的往复运动,并对平台的纵摇起决定性作用;
(2)风、浪、流联合作用下平台运动响应极值大于其单独作用之和,这是因为平台上体和张力腿系统之间存在耦合效应,比如平台远离平衡位置时会减小平行张力腿系统对平台垂荡方向和纵摇方向的刚度贡献,而纵荡方向改变不明显,各荷载对平台各方向运动响应贡献比例如表6所示;
(3)由图8可知,附加浮筒后平台各工况下的纵荡和垂荡响应明显减小;各工况下平台的纵摇响应大小不一,但总体取值较小。以在张力腿100 m处附加0.2倍上体净浮力浮筒为例,风、浪联合作用下,平台纵荡峰值减小14.20%,垂荡峰值减小27.28%,纵摇极值减小 18.58%;
(4)随着附加浮筒位置降低,纵荡方向:风或流单独作用时平台响应均线性递增,波浪载荷作用时平台响应先增后减,联合作用时平台响应先减后增,在300 m时为最小值;垂荡方向(负值,取绝对值来衡量大小):风和流对应线性递增,波浪对应先减后增,联合对应先减后增,在300 m时为最小值;纵摇方向:对风或流作用影响不明显,波浪对应先减后增,会超过无附加浮筒响应,联合对应100 m位置响应最小,无明显变化规律;
(5)由图9可以看出,随着附加浮筒净浮力减小,纵荡方向:风和流对应响应明显递增,波浪对应小幅递减,联合对应明显递增;垂荡方向:风和流对应明显递增,波浪对应明显递减,联合对应明显递增;纵摇方向:对风或流作用影响不明显,波浪对应先减后增,会超过无附加浮筒响应,在400 m位置为最小值,联合对应先减后增,会超过无附加浮筒响应,在300 m位置为最小值。
5 随机波浪作用下平台的运动响应
前文表3中给出了我国南海某海域可以用JONSWAP谱表达的波浪参数,同时考虑风、流以及随机波浪联合作用,模拟得出附加浮筒平台和原传统式平台的运动响应对比,如图10~图12所示。
需要说明的是,数值分析模型中TLP平台的初始重心位置为(0,0,13.33 m),垂荡响应大小等于 13.33 m-重心垂荡时程坐标。
由图10(a)可知,附加浮筒后TLP平台纵荡响应及纵荡慢漂响应明显减小;由图10(b)和图10(c)可知,附加浮筒后TLP平台纵荡波频响应有所增大,但响应频率分布特征没有明显变化。
由图11(a)可知,附加浮筒后TLP平台垂荡响应及垂荡慢漂响应明显减小;由图11(b)和图11(c)可知,附加浮筒后TLP平台垂荡波频响应及频率特征没有明显变化。
由图12(a)可知,附加浮筒后TLP平台纵摇慢漂响应略微减小,而总的纵摇响应却略有增大;由图12(b)可知,附加浮筒下平台纵摇响应的波频成分有所增加,但仍处于小值;由图12(c)可知,附加浮筒后平台的纵摇响应的低频部分所占比例增加了,但同时使得平台出现了更高的响应频率。
以上变化的具体大小将在下文的统计值中予以说明。

如表6所示为平台运动响应的统计信息,可知:
(1)附加浮筒前后,平台纵荡低频响应均方差平方与总体均方差平方比值由80.81%增加为82.95%,响应均值减小了18.65%,响应极值减小了15.17%;
(2)附加浮筒前后,平台垂荡低频响应均方差平方与总体均方差平方比值由88.34%增加为89.55%,变化不大,响应均值减小了43.56%,响应极值减小了35.01%;
(3)附加浮筒前后,平台纵摇低频响应均方差平方与总体均方差平方比值由7.35%增加为8.36%,响应均值减小了21.36%,响应极值增加了5.72%。
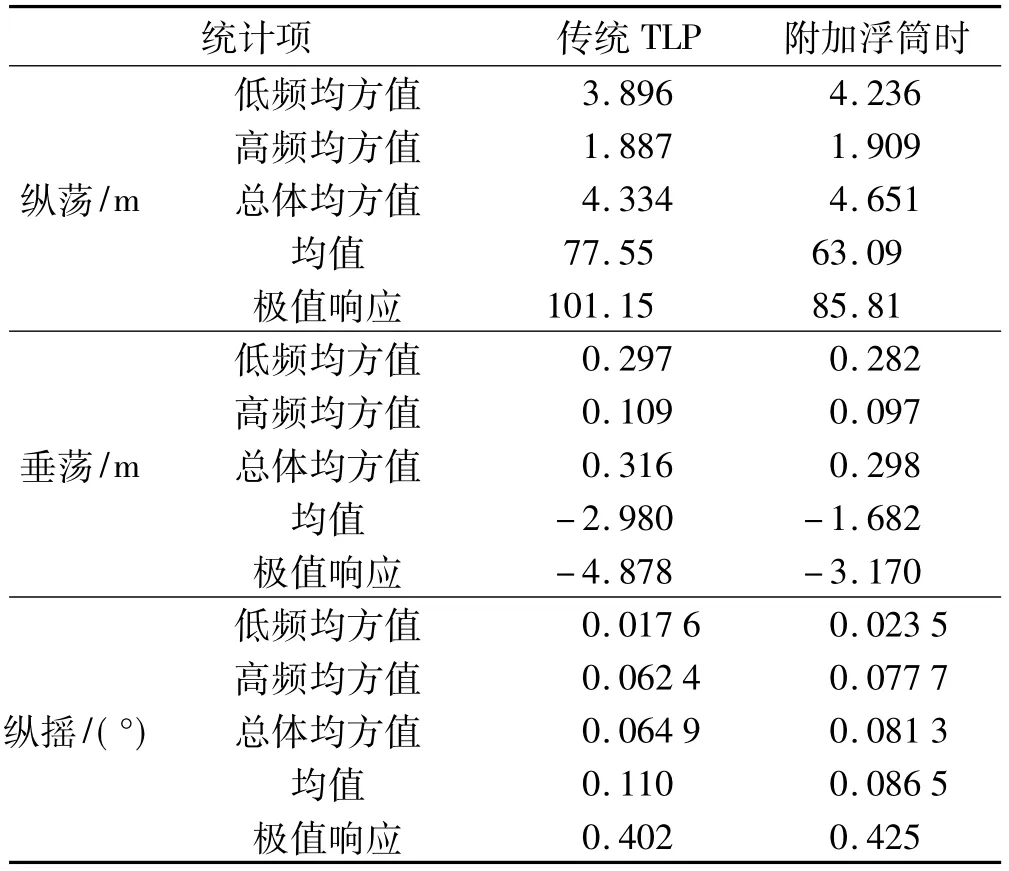
表6 平台运动响应统计值Tab.6 Dynamic response statistical values of TLP
6 结论
本文通过在张力腿上附加浮筒来改良TLP平台的性能,建立了改良平台的多体耦合运动模型并用数值模拟的方法进行了响应分析。由以上分析内容可以到以下几点主要结论:
(1)考虑风、浪、流的联合作用与分别考虑风、浪、流的作用并求和相比,前者会激起更大的TLP平台运动响应极值,增量分别为纵荡(0.4%)、垂荡(94%)、纵摇(29%)。风、流、浪分别作用下TLP平台各方向运动响应极值比约为纵荡 (0.42∶0.48∶0.1),垂荡(0.33∶0.55∶0.12),纵摇(0.22∶0.13∶0.65)。这表明,风和流荷载主要引起了平台的纵荡(90%)和垂荡(88%),而波浪主要引起平台的纵摇(65%)。这是因为风、流荷载为主要的水平荷载作用,而张力腿系泊系统在水平方向给平台提供的刚度很小,使得平台纵荡很大,同时由于张力腿的系泊作用,平台较大的纵荡就会引起较大的垂荡,而波浪为具有一定周期性的时变力,在平台纵摇上的贡献较大。
(2)对不同工况数值模拟得出,附加浮筒可以显著降低各环境荷载单独及联合作用下的张力腿平台的纵荡和垂荡响应极值,作用效果受到附加浮筒就位水深和净浮力的影响,净浮力大小的影响更为明显。附加浮筒对平台的纵摇没有明显一致的作用,随着附加浮筒不同的净浮力和就位水深而增加或减小。以在张力腿100 m处附加0.2倍上体净浮力浮筒为例,风、浪联合作用下,平台纵荡峰值减小14.20%,垂荡峰值减小27.28%,纵摇极值减小18.58%,其他工况的具体效果可以从图8和图9中得出。
(3)在风、流和随机波浪联合作用下,附加浮筒平台和未附加浮筒平台在各方向运动响应极值比分别为纵荡(0.85∶1)、垂荡(0.65∶1)、纵摇(1.06∶1),这表明附加浮筒能够明显减小平台的纵荡(减小15.17%)和垂荡(35.01%)极值响应,而平台的纵摇会略有增加。各方向响应均值会明显减小,纵荡方向减小了18.65%,垂荡方向减小了43.56%,纵摇方向减小了21.36%。分析可知,附加浮筒主要减小了平台在各方向上的慢漂响应,而对平台在该方向上的波频响应的大小及频率成分没有明显影响,还会使得纵摇响应极值有所增加。
[1] Donley M G,Spanos P D.Stochastic response of a tension leg platform to viscous drift forces[J].Journal of Offshore Mechanics and Arctic Engineering,1991,133(2):148-155.
[2]Vickery P J.Wind-induced response of tension leg platform:theory and experiment[J].Journal of Structural Engineering,1995,121(4):651-663.
[3] Kim M H,Tahar A,Kim Y B.Variability of TLP motion analysis against various design methodologies[C]//Proceedings of the International Offshore and Polar Engineering Conference(ISOPE01). Stavanger, Norway,2010:467-473.
[4]胡志敏,董艳秋,张建民.张力腿平台水动力参数计算[J].海洋工程,2002,20(3):14-22.
[5]曾晓辉,沈晓鹏,刘 洋,等.考虑多种非线性因素的张力腿平台动力响应[J].海洋工程,2006,24(2):82-88.
[6]曾晓辉,刘 洋,沈晓鹏,等.有限位移下张力腿平台的非线性动力响应[J].工程力学,2007,24(3):179-184.
[7] Taflanidis A A,Angelides D C,Scruggs J T.Simulationbased robust design of mass dampers for response mitigation of tension leg platforms[J].Engineering Structures,2009,31(4):847-857.
[8]Yang C K,Kim M H.Transient effects of tendon disconnection of a TLP by hull-tendon-riser coupled dynamic analysis[J].Ocean Engineering,2010,37(8-9):667-677.
[9]赵连恩,谢永和.高性能船舶原理与设计[M].北京:国防工业出版社,2009.
[10]王 科,许 旺.FPSO型采油平台波浪漂移力的分析研究[J].哈尔滨工程大学学报,2008,29(12):1261-1265.
[11]闫功伟,欧进萍.基于AQWA的张力腿平台动力响应分析[J].东南大学学报(自然科学版),2009,39(增刊(Ⅱ)):304-310.

