基于核形态成分分析的齿轮箱复合故障诊断研究
杨 杰,郑海起,关贞珍,王彦刚
(石家庄军械工程学院 石家庄 050003)
当齿轮箱出现故障时,有时可能不只存在一种故障,可能是多种故障状态并存,盲源分离为齿轮箱多故障并存的分离提供了一种新的方法,已成功应用到齿轮箱故障诊断中[1-2]。
在盲源分离算法中,经典的独立成分分析(ICA)方法假设源信号是独立统计的。虽然目前ICA方法在许多应用中已证明是成功的[3-5],然而,ICA基于统计独立的假设条件,并不适用于所有的情况。特别是在实际应用中,很多信号或图像具有稀疏性,或者可以对信号或图像进行适当的变换,使其在变换域中具有较好的稀疏性。在稀疏成分分析(Sparse Component Analysis,SCA)中就利用了这一点[6-7]。最近,Starck 等[8-9]另辟新径,提出了另外一种基于信号稀疏表示的分离方法——形态成分分析(Morphological Component Analysis,MCA),该方法的主要思想是利用信号组成成分的形态差异性(可以由不同的字典稀疏表示)进行分离。目前,该方法在图像处理[10-12]和脑信号分离[13]中已经有一些应用,在机械信号处理方面尚未见报道。
当利用齿轮箱振动信号进行故障诊断时,传感器测取的信号是各种源信号的混合信号,这些源信号在传输过程中往往会发生不同程度非线性畸变、混叠等现象,而且这种非线性畸变在齿轮箱发生复合故障时尤为明显。而MCA假设源信号是线性混叠的,因此不能有效地分离出非线性过程的源信号,从而得不到理想的诊断效果。
本文结合核函数把基于MCA的线性盲分离方法拓展到非线性混叠情况,给出了一种非线性混叠信号盲分离算法。该算法首先将混叠信号映射到高维核特征空间,其次,在核特征空间中构造一组正交基,通过这组正交基将高维核特征空间的信号映射到这组正交基张成的参数空间中,从而把非线性混叠信号盲分离问题转化为参数空间的线性混叠信号盲分离问题。最后,在参数空间中,应用基于信号稀疏特性的线性盲分离方法对信号进行分离。该算法收敛精度较高,稳定性好。
1 形态成分分析的基本理论


Stark 等[16]在 BCR(Block-Coordinate-Relaxation)方法的基础上,给出了MCA的数值实现:
(1) 初始化迭代次数Lmax及阈值δk=λk·Lmax/2
(2)Whileδk>λk/2
fork=1,…,n
假设sk'≠k不变,更新sk:
·软阈值法计算系数αk,阈值为δk,得到系数;
·由sk=Φk重构sk。
更新阈值δk=δk-λk/2。
MCA算法只能分离同一信号中具有不同形态的信号分量。Boin等[17]将 MCA扩展到多通道数据情况下,提出了GMCA(Generalized MCA)算法,GMCA是一种快速有效的盲源分离方法,它充分利用了形态多样性和稀疏性的特点,把源看作是形态分量的线性组合,并利用稀疏性来估计源和混合矩阵,取得了较好的实验结果。Xinyi[13]将该方法应用到了脑信号分离中。
对于线性混叠模型:

设源信号是统计独立的,且每个源信号sk是不同形态成分的线性组合:

Tk和Rk分别表示与冗余字典Φk相关的正逆变换,在上述优化问题中,估计第k个源信号中的信号分量由前文提到的 MCA 算法实现,得 GMCA算法如下:
(1) 初始化递归次数Lmax和阈值:∀k,δk=λk·Lmax·λk/2
(2)Whileδk>λk/2
Fork=1,…,n
(3) 假设sk'≠k和αk'不变,更新sk:
·计算源信号sk的粗略估计;
·由阈值δk和MCA算法计算的稀疏分解,得到分解系数{αk,j};
(4)设源信号不变,更新A;
(5) 对∀k,重新归一化αk,sk和δk;
(6) 对∀k,减小阈值δk=δk-λk/2。
2 核形态成分分析算法
2.1 核形态成分分析算法
一般化的非线性混叠信号模型可描述如下:

即xi(t)=fi[s1(t),s2(t),…,sn(t)],F=[f1(·),f2(·),…,fn(·)]T。将混叠信号{x(t),t=1,2,…,T}∈Rn用Φ(·)映射到高维特征空间中,即:

并在高维特征空间Γ中选择一组基:

构造如下正交基:

则可通过该正交基将Φ(x(t))在特征空间中参数化为d维信号:

由于直接计算被映射的数据Φx和Φv是困难的,为此引入核函数k(·,·)满足k(a,·b)=Φ(a)T·Φ(b),则有:
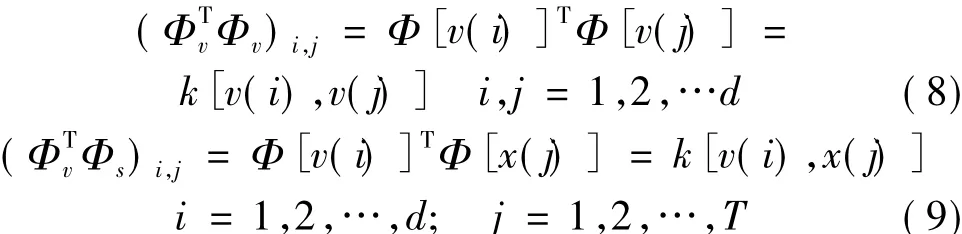
Ψ[x(t)]即是被映射到参数空间中的数据,假设选择的核函数k(·,·)使Φ(·)=F-1(·),则由式(4)、式(5)、式(6)、式(7)可得:

即Ψ(x(t))是s(t)的线性混叠信号。把GMCA算法应用于被映射到参数空间中的数据Ψ(x(t)),得到本文提出的核形态成分分析算法(KGMCA)如下:
(1) 通过特征选择算法从{x(t),t=1,2,…,T}∈RN中选择{v(t),t=1,2,…,d}∈RN;
(2)由式(7)、式(8)和式(9)计算被映射到参数空间中的数据Ψ(x(t))(t=1,2,…,T};
(3)用GMCA算法对Ψ(x(t))进行盲分离,得到源信号。
2.2 特征选择算法
下面研究KGMCA算法步骤1中特征空间Γ中基Φv的选择问题[18]。
设在输入空间(即混叠信号空间)中选择的特征向量数为L,特征向量标记为,在特征空间中的映射为Φ()=,1≤j≤L,给定的特征向量集S={,…,},则输入空间中任一向量xi在特征空间中的映射可以表示为特征向量集S的线性组合:

其中:ai=(,…,)t为参数向量。现在的问题是对于给定的S,求解ai,使得Φi的估计值以最大概率接近Φi,为此,构造如下的评价函数:

用矩阵形式重写式(12),从而最小化δi的问题可表示为内积形式:

其中:KSS为特征向量内积的方阵,KSi为xi与特征向量集S的内积矩阵。问题转化为在输入空间X中寻找S,使其满足式(13),即:

定义适应度函数:

则式(14)等价于:

式(16)可通过递归算法求解,从而得到S,即{v(t),t=1,2,…,d}∈Rn。
3 仿真信号分析
为了检验KGMCA盲分离算法的有效性,进行了如下的仿真,取m=3,n=3,即三个传感器、三个源信号的盲分离。
设三个源信号分别为:

其中:t=1,2,…,1 024,s1(t)的 Gauss脉冲重复频率 0.02 Hz,Gauss脉冲中心频率0.2 Hz,持续时间长度■5 s,简谐波频率0.01 Hz,s2(t)的Gauss脉冲重复频率0.05 Hz,Gauss脉冲中心频率0.4 Hz,持续时间长度■5 s,简谐波频率0.035 Hz,n(t)为随机噪声,信噪比为3 dB,信号采样频率为1 Hz。经非线性关系x(t)=A1tanh(A2s(t))混叠,其中,随机选取混叠矩阵为:

将三路信号非线性混叠并叠加3dB的高斯白噪声,源信号及混叠信号分别如图1(a)和(b)所示,构造Fourier字典和基于8阶消失矩Symlet小波字典,应用KGMCA算法的信号分离结果如图1(c)。
由图1(c)可以看出,源信号被较好地分离出来,且噪声较小。
由于核函数方法的实质就是实现一种由输入空间到特征空间的映射,通过定义特征变换后样本在特征空间中的内积来实现一种特征变化。这就是说,通过引入核函数就可以实现所有的计算,而不需要知道非线性函数和特征空间(核空间)的具体形式。因此KGMCA算法不受非线性函数的具体形式的约束,具有较广泛的适用性。

图1 源信号、混叠信号和分离结果波形图Fig.1 Sources、mixtures and separation result
4 齿轮箱复合故障信号分析
在某型单级齿轮箱上进行试验验证。该系统由电机带动输入轴,输出轴带动负载。主动齿轮齿数Z1=30,被动齿轮齿数Z2=50,输入轴轴承为6206型单列向心滚动轴承,输出轴轴承为7207型单列向心滚动轴承,在主动齿轮的一个轮齿根部加工一道宽为0.5 mm,深为1.5 mm的小槽模拟齿根裂纹故障。轴承故障是在输入轴轴承内圈和外圈通过线切割实现的,对振动信号在时域里进行等时间间隔采样,采样频率为12800 Hz,测量时转速为1 200 r/min,采样时间长度为0.25 s。齿轮故障频率为转频20 Hz,6206型轴承内径为9.5 mm,外径为 46.5 mm,接触角为 0°,滚动体数目为 9,根据轴承的结构尺寸和工作转速,可以计算出轴承不同元件的故障特征频率:内圈故障特征频率108.4 Hz,外圈故障特征频率为71.6 Hz。
在输入轴两端的轴承座和输出轴一端的轴承座上各安装一个传感器,传感器的型号为B&K4508加速度传感器,三个传感器采集的振动信号频谱如图2(a)、图2(b)和图2(c)所示,可以看出采集信号的几个故障特征频率在每一个频谱图上混叠,难以确定哪些故障存在。而且由于齿轮箱系统为典型的含间隙、油膜和时变刚度的多体弹性非线性动力学系统[19],传统的线性盲分离方法不再适用。

图2 三路传感器采集信号的频谱图Fig.2 Spectrum of the vibration signals
为了匹配所分析信号的结构特征,需要根据信号性质或先验知识设计字典。目前,已经构造了多种过完备字典,常用的字典有Dirac字典、Fourier字典、小波字典、小波包字典和Gabor字典等。其中,Dirac字典适合匹配振动信号中的脉冲成分;Fourier字典是典型的频率字典,是频率过离散的简谐三角函数集合,适合分析简谐信号;小波字典是典型的时间-尺度字典,适合分析具有等比例带宽性质的信号。
如果轴承的内圈或外圈有损伤,轴旋转时,这些零件在接触过程中会发生机械冲击。齿轮振动信号主要由齿轮的啮合效应和旋转运动引起,损伤齿轮振动信号中还会出现冲击和瞬态振动特征。为了有效匹配分析齿轮箱振动信号的特征结构,根据齿轮箱振动信号特点,构造了Fourier字典、Dirac字典和基于8阶消失矩Symlet小波的标准正交小波字典以及持续一定时间长度覆盖一定频率带宽的波形函数的组合,分别用以匹配振动信号中的简谐振动、冲击和其他瞬态振动现象。
采用KGMCA算法对采集的三路振动信号进行盲分离,图3分别为分离出的三个源信号的频谱图。

图3 KGMCA分离信号频谱图Fig.3 Spectrum of the separated signals by KGMCA
从图3(a)中能看出20.5 Hz和41 Hz的频率成分,这与齿根裂纹故障特征频率(20 Hz)及二次谐波(40 Hz)接近,由此可认为齿根裂纹故障被有效的分离出来;从图3(b)中能看出71.5 Hz和143 Hz的频率成分,这与滚动轴承外圈故障特征频率(71.6 Hz)及二次谐波(153.2 Hz)接近,由此可认为外圈故障被有效的分离出来。从图3(c)中能看出108.5 Hz和217 Hz的频率成分,这与滚动轴承内圈故障特征频率(108.4 Hz)及二次谐波(216.8 Hz)接近,其他频率幅值成分较小,由此可认为内圈故障被分离出来。经上述分析得出,本文提出的算法能较好地分离出齿轮和滚动轴承的故障特征。
非线性盲源分离算法有:核独立成分分析(KICA)和非线性主分量分析(PCA)等,这些方法在对应的条件和约束下都能获得最佳性能。非线性PCA方法需先对观察信号做预白化的处理,然后最小化非线性PCA准则来获得相应的分离算法。文献[20]中,Oja给出了非线性PCA的一种实现算法,但这一算法收敛速度慢,精度低,且步长的选择不易把握。而KICA基于统计独立的假设条件,并不适用于所有的情况。与这些方法相比,KGMCA算法具有收敛速度快、精度高、对带噪混叠信号分离效果好的特点,但是需要人为设定用于信号分离的字典,如果字典选择不当则分离效果不理想,这是其缺点所在。
5 结论
形态成分分析方法是有别于稀疏成分分析的一种基于稀疏表示的线性混叠信号分离方法,它利用追踪算法来搜索信号最稀疏的表示将产生理想的分离效果。本文结合核特征空间,把这种方法推广到了非线性混叠情况,给出了一种非线性混叠信号盲分离算法。仿真结果表明该算法是有效的,并应用KGMCA算法对设有3种复合故障的齿轮箱振动信号进行分析,成功分离并找到了故障特征,从而验证了该方法在齿轮箱复合故障诊断中的有效性。
然而由于MCA崭新的理论面貌和独到的应用特点,还存在很多问题值得深入研究[21],如:选择何种类型的原子来构造合适的字典和级联字典族;研究好的阈值选择策略提高算法的收敛性;建立基于MCA稀疏分解的评价方法等。
[1]王 宇,迟毅林,伍 星.基于盲信号处理的机械噪声监测与故障诊断[J].振动与冲击,2009,28(6):32-41.
[2]李加文.盲信号理论及在机械设备故障检测与分析中的应用研究[D].上海:上海交通大学,2006.
[3]田 昊,唐力伟,田 广.基于核独立分量分析的齿轮箱故障诊断[J].振动与冲击,2009,28(5):163-164.
[4]李 好.基于独立分量分析(ICA)齿轮传动装置振动信号研究[D].西安:西安科技大学,2009.
[5]苏永振,袁慎芳.基于独立分量分析的多源冲击定位方法[J].振动与冲击,2009,28(8):134-137,157.
[6]Georgiev P G,Theis F,Cichocki A.Sparse component analysis and blind source separation of underdetermined mixtures[J].IEEE Trans.Neural Network,2005,16(4):992-996.
[7]Zibulevsky M,Pearlmutter B.Blind source separation by sparse decomposition in a signal dictionary[J].Neural-Computation,2001,13(4):863-882.
[8]Starch J L,Elad M,Donoho D.Redundant multiscale transforms and their application for morphological component separation[J].Advances in Imaging and Electron Physics,2004,132(82):287-348.
[9] Starck J L,Moudden Y,Robin J.Morphological component analysis[C]//Proc of SPIE,2005,59(14):1-15.
[10]耿瑞敏,练秋生,孙马秋.基于形态学成分分析的指纹分离[J].计算机工程与应用,2008,44(16):188-190.
[11]张 涛,洪文学.基于自适应字典选择的MCA图像修复方法[J].光学技术,2010,36(5):672-677.
[12]付 蓉,李 洁,高新波.基于形态学成分分析的静态极光图像分类算法[J].光子学报,2010,39(6),1034-1040.
[13] Yong X Y,Ward R K,Birch G E.Generalized morphological component analysis for EEG source separation and artifact removal[C]//Proceedings of the 4th International IEEE EMBS Conference on Neural Engineering Antalya,Turkey,2009:343-347.
[14] Chen S.Basis pursuit[D].Department of Statistics,Stanford University,Stanford,CA,1995.
[15] Mallat S,Zhang Z.Matching pursuit with time frequency dictionaries[J].IEEE Transactions on Signal Processing,1993,41(12):3397-3415.
[16]Bruce A,Sardy S,Tseng P.Block coordinate relaxation methods for nonparamatric signal denoising[C]//Proceedings of the SPIE-The International Society for Optical Engineering 3391,1998:75-86.
[17] Bobin J,Moudden Y,Starck J L.Enhanced source separation by morphological component analysis[C]// IEEE International Conference on Acoustics Speech and Signal Processing Proceedings,2006:833-836.
[18] Baudat G,Anouar F.Kernel based methods and function approximation[C]//Proc IJCNN,Washington,DC,2001:1244-1249.
[19]刘国华,赵继学,李亮玉.含间隙和时变刚度的齿轮机构振动特性分析及实验研究[J].机械设计,2010(2):43-49.
[20] Oja E.The nonlinear PCA learning rule in independent component analysis[J].Neural Computing,1997,17:25-46.
[21]李 映,张艳宁,许 星.基于信号稀疏表示的形态成分分析:进展和展望[J].电子学报,2009,37(1):146-152.

