基于遗传算法与能量方程的粘弹性隔震装置参数优化分析

郭一峰，徐赵东，涂 青

（1.东南大学 混凝土及预应力混凝土结构教育部重点实验室，南京 210096；2.苏州工业园区设计研究院股份有限公司，江苏 苏州 215021；3.中南市政工程中南设计研究院，武汉 430010）

结构的振动控制主要包括主动控制和被动控制。主动控制为有源控制，能够根据最优控制理论达到全状态最优反馈增益要求的控制力，但是该方法在实际应用中其经济性和适用性并不能够很好满足。被动控制为无源控制，经济性和适用性能够很好的满足实际需要，但是其设计还存在着很多的问题。粘弹性阻尼器（VED）是一种典型的被动控制装置，它具有经济实用、性能可靠、安装方便等特点，具有广阔的应用前景，因此非常有必要对VED的参数设计方法进行深入的研究。在VED的设计中，由于被动控制的反馈存在种种的约束，无法直接应用最优控制理论，而只能通过其它的一些方法进行参数设计［1-3］：如基于时程分析法、随机振动理论和现代控制极点配置理论等等进行参数设计；采用的优化算法有复形法、Fmincon函数法和遗传算法等等。但是，上述的方法都是对简单的结构模型（层间模型）或者将复杂的结构模型等效成简单的模型进行参数优化。对于复杂结构模型这种等效的优化结果是否具有实际效果还待进一步研究。此外，上述优化方法所采用的目标函数对于地震波比较敏感，不同的地震波，其参数优化的结果也是不一样的。本文将基于遗传算法和能量方程，采用结构全模型进行参数优化，以解决上述方法在模型处理较简单和对地震波敏感两个方面的缺点。

1 粘弹性阻尼器优化计算参数

加入粘弹性隔震装置结构的动力方程如下：

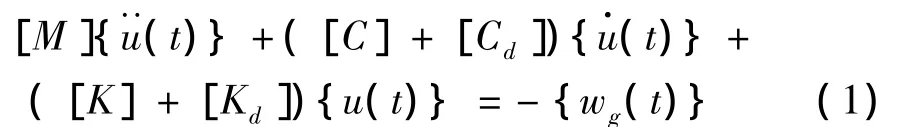
由上式可见，粘弹性隔震装置的隔减震性能仅和等效刚度［Kd］和等效阻尼［Cd］有关。根据文献［4］，可以求得粘弹性隔震装置的等效刚度和等效阻尼：

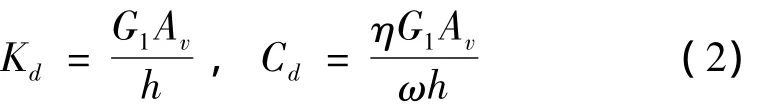
由上式可知，影响粘弹性隔震装置隔减震性能的因素为：G1Av/h、η以及结构的基频ω。

文献［3］中，将储能模量G1、损耗因子η、粘弹性层的剪切面积Av和粘弹性层的厚度h作为多维隔减震装置的计算参数，这种考虑参数影响的方法过于理想，同时也是不切合实际。粘弹性材料的损耗因子η与材料本身性质有关，这个参数可根据具体的环境条件和生产厂家提供的数据选定；结构的基频ω受等效刚度Kd的影响，即与G1Av/h有关。此外，由式（2）可知等效刚度和等效阻尼仅仅与Av/h的值有关，而与具体的Av和h的值无关，将Av和h直接作为参数来优化是不合理的；粘弹性层的剪切面积Av和粘弹性层的厚度h需要根据实际结构需求来具体选取。通过以上分析，本文将Av/h作为优化参数变量，结合实际材料类别确定的储能模量G1和损耗因子η进行优化，然后依据结构实际要求来确定粘弹性层的剪切面积Av和粘弹性层的厚度h。

2 能量方程与优化目标函数

文献［2-3］中采用的优化目标函数是加速度、位移、力等等参数的线性组合，该种方法对地震波数据很敏感，选取不同的地震波，计算所得的加速度、位移和力等参数是不同的，导致优化结果对于不同的地震波也是不相同的［3］。研究表明［4］，结构在地震作用下的响应不仅与结构自身的动力特性有关，还与地震动三要素（幅值、频谱和持时）紧密相关。而结构地震反应的能量分析方法就是一种能够较好的反应结构在地震作用下自身动力特性和地震动三要素对结构反应影响的方法。

在地震作用下，多自由度结构的运动微分方程为：

式中：［M］、［C］、［F］分别为质量矩阵、阻尼矩阵、恢复力向量；{}、{}、{X}分别为结构的加速度、速度和位移为地面运动加速度；{δ}为单位列向量。

对式（1）两端在相对位移下进行积分，并令{X}={}dt，则得：

令：

结构动能：

阻尼耗能：

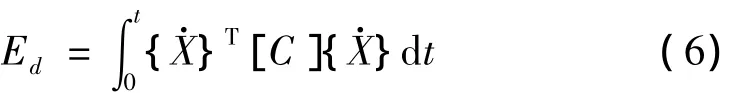
滞回耗能Eh+弹性变形能Es：

地震输入能：

则式（2）可以写成：

式（9）为多自由度体系的相对能量反应方程。

研究表明［4］，在大量地震能量输入结构后，仅很少部分转化为动能和弹性应变能，大部分能量通过阻尼和塑性变形耗散，同时由于结构的塑性变形的不可恢复性，通常将结构的滞回耗能视为结构破坏能量的指标，当结构的滞回耗能能力大于地震输入的能量时，结构是安全的，否则将发生倒塌。结构的动能和弹性应变能在地震过程中相互转化，地震反应结束后均为0。因此，式（9）可以写为：

式（10）表明，在地震的全过程中，地震输入的总能量最终被阻尼和滞回耗能消耗掉。

由式（10）可知，要减小结构的滞回耗能，可通过两种方式：①增加阻尼耗能Ed；②减少地震输入能Ein。

定义函数：α=1-Ed/Ein由式（4）～式（10）可知，地震输入能Ein越小，阻尼耗能Ed越大，α值越小，也就是结构的滞回耗能越小。参数优化的最终目标是在合适的参数下结构的滞回耗能越少越好。

参数优化目标函数取为：

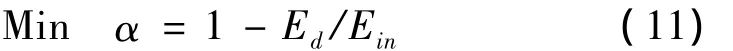
一个设计方案必须满足的条件，称为约束条件。多维隔减震装置的主要组成材料是粘弹性材料，需要控制装置变形，使其不能超过粘弹性材料的极限变形。控制装置变形，实际就是控制装置的刚度，从式（2）可看出，控制Av/h大于某一数值，可保证多维隔减震装置变形不会超过粘弹性材料的极限变形；控制Av/h小于某一数值，可以保证多维隔减震装置具备隔震效果。约束条件如下：

综上所述，优化数学模型如下：

求Av/h

3 遗传算法与优化方法

遗传算法（Genetic Algorithm）是一类基于达尔文的进化论和孟德尔的遗传学说的模拟自然优化选择和有性繁殖过程的一种搜索最优解的方法，它能方便的进行多目标变量优化。遗传算法能在概率意义下收敛到问题的全局最优解，故被广泛认为是一种稳健的全局搜索算法。遗传算法一般包括编码、产生群体、计算适应度值、再生、交叉、变异等操作。本文运用MATLAB编制了相应的遗传算法程序。

本文结合遗传算法优化和ANSYS建模计算二者的优点，对多维隔减震装置的参数进行优化，其具体的优化过程如图1所示。

图1 优化流程Fig.1 Optimization flow

4 数值分析

如图2所示的双层柱面网壳，结构参数为：跨度S=39 m，矢跨比f/S=0.3，壳长L=63 m，壳厚h=2 m，网格尺寸3 m×3 m。杆件规格：上弦杆Φ114×4.0，下弦杆Φ89 ×4.0，腹杆Φ76×4.0，各杆均为热轧无缝钢管，钢材为Q235钢，材料弹性模量E=206 GPa。网壳上弦屋面恒荷载为1.0 kN/m2，节点质量系数为0.3，输入地震波为三向Taft波，时间间隔为0.02 s，持时30 s，最大加速度为400 gal。柱面网壳的支承形式为：无控状态下，两纵边采用三向固定铰支座，两端部只设置垂直约束；有控状态下，两纵边在横向设置粘弹性隔震装置，两端部仍采用垂直约束。粘弹性隔震装置选取粘弹性材料参数取值为：G1=1.0 ×106N/m2，η=1.4。

图2 柱面网壳Fig.2 Cylindrical latticed shell

4.1 优化结果

经优化计算，最终优化结果为：Av/h=3.2。

结构有控状态下地震总输入能和阻尼总耗能时程曲线如图3所示，无控和有控结构地震总输入能对比如图4所示。从图3中可以看出：在7s前，随时间增加阻尼耗能急剧增加；10 s后阻尼耗能渐渐趋于一个常数，说明阻尼耗能在10 s以后增加较少，地震能量主要由结构滞回耗能消耗；阻尼总耗能约占地震输入总能量的28.6%。图4表示无控和有控结构地震总输入能对比。由图4可以看出，无控结构的地震总输入能大于有控结构约30%。粘弹性阻尼器装置使整个结构刚度降低，自振周期延长，因此地震总输入能减少。

无控和有控结构节点绝对位移（三向位移矢量和）与杆件最大应力对比如图5、图6和表1所示，有控结构较无控结构节点最大绝对位移和杆件最大应力都得到了较好的控制，节点最大位移和杆件最大应力的控制率分别为33.4%和40.7%。这表明参数优化的结果是合理有效的，加入粘弹性隔震装置能有效的减小结构在地震动作用下的响应，体现了很好的隔震和减震的双重作用。

图6 杆件最大应力时程曲线Fig.6 Time-history curve of the max stress

为了比较优化效果，选用最优值与随机选取的非最优值进行分析，其中最优值为Av/h=3.2；随机选取非最优值Av/h=6.0。由图7及8可知，最优值控制下的结构绝对位移及杆件最大应力要小于非最优值控制下的值；最优值控制下的结构杆件最大应力为119.3 MPa，非最优控制下的值为168.2 MPa，最优值低于非最优值29.1%；节点最大位移，最优值也低于非最优值20.8%。这表明参数优化的结果是合理的。

表1 无控和有控结构对比表Tab.1 the comparison between the structure with controlled and no controlled

4.2 地震波影响

地震波是一种频带较宽的非平稳随机振动，地震动的主要特性可以通过地震动幅值、频谱和持时三个要素来表示。文献［2-3］中所采用的目标函数优化所得的结果受所选取的地震波的影响较大。为了考察本文所提出的目标函数对地震波的敏感性，本文将选取适用于二类场地土的四种地震波，采用文献［3］的优化目标函数进行优化计算所得的结果（工况一）与本文所采用的优化目标函数所得的结果（工况二）进行对比分析。对比结果如表2所示。

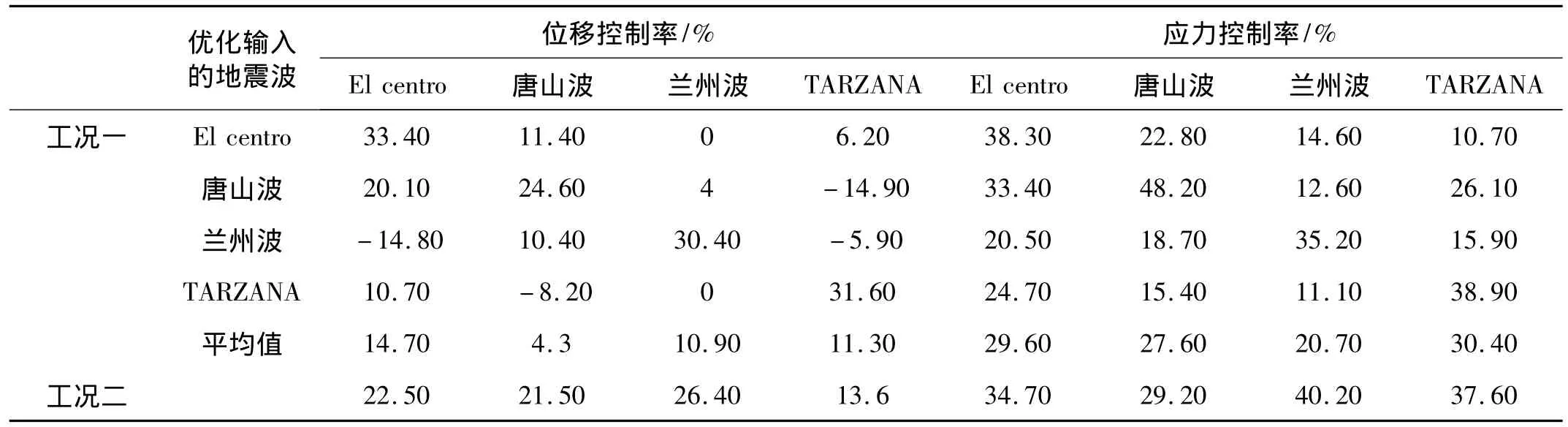
表2 工况一与工况二优化结果对比Tab.2 The comparison between the case1 and case2

以工况一的唐山波（优化过程输入的地震波）为例，由表2可知，结构在4种地震波下的应力都得到了控制，但是结构在输入TARZANA时，位移控制率是负值，这表明工况一中基于唐山波优化所得的粘弹性阻尼器的参数并不适用于TARZANA波。工况一的其他三种波也存在这样的现象。这表明文献［3，8］所采用的优化目标函数对地震波是比较敏感的，在某一地震波下优化所得的参数不一定适合另一个地震波。

工况二采用的参数是基于TAFT波优化所得的，从表2可以看出在各种地震波下，结构的位移和应力都得到了较好的控制。这表明目标函数式（11）对地震波敏感性显著减小。

本文还将工况一下四种地震波优化计算所得的参数的平均值作为粘弹性阻尼器的参数，计算所得的控制率如表2所示，可以看出位移和应力也得到了有效的控制。但是这种多次优化取平均值的方法需要花费很多的时间，而控制效果却比工况二要低。

5 结论

本文基于能量方程研究了粘弹性阻尼器装置的参数优化问题，提出了基于遗传算法的目标优化函数，建立了粘弹性阻尼器装置参数优化模型。以柱面网壳隔减震为例，基于遗传算法和能量方程，采用ANSYS和MATLAB并行对其进行参数优化分析，并分析了该方法对地震波的敏感性，得出以下结论：

（1）基于能量方程的目标函数，采用遗传算法对粘弹性阻尼器参数优化是合理有效的；

（2）采用优化所得的参数的粘弹性阻尼器加设到结构中能有效的减小结构在地震动作用下的响应，体现了很好的隔震和减震的双重作用；

（3）本文提出的目标函数对地震波敏感性显著减小，该目标函数具有较强的适用性。

［1］周晓峰，陈福江，董石麟.粘弹性阻尼材料支座在网壳结构减震控制中性能研究［J］.空间结构，2000，6（4）：21-27.

［2］凌和海，薛素铎，庄 鹏.减震结构中的粘弹性阻尼器参数优化［J］.世界地震工程，2005，21（3）：126-130.

［3］涂 青.隔减震结构中粘弹性阻尼支座的参数优化［J］.东南大学学报（自然科学版），2009，39（1）：73-77.

［4］周福霖.工程结构减震控制［M］.北京：地震出版社，1997.

［5］Park K S，Koh H M，Hahm D.Intergrated optimum design of viscoelastic damped structuralsystems［J］.Engineering Structures，2004，26：581-591.

［6］ Singh M P，Moreschi L M.Optimal placement of damper for passive response co-ntrol［J］.Earthguake Engineering and Structural Dynamics，2002，31：955-976.

［7］卜国雄，谭 平，周福霖.基于能量法的TMD参数优化设计［J］.华中科技大学学报，2008，25（2）：26-30.

［8］赵 波.粘弹性阻尼材料支座在网架结构减震控制中的性能研究［D］.西安：西安理工大学，2007.

［9］ Kwon Y D，Kwon S B，Jin S B，et al.Convergence enhanced genetic algorithm with successive zooming method for solving continuous optimization problems ［J］.Computers and Structures，2003，81（1）：1715-1725.