晃动的流体对渡槽结构振动的抑制与放大效应

李遇春，邸庆霜

（同济大学 土木工程学院 水利工程系，上海 200092）

渡槽在地震或脉动风作用下，渡槽结构会发生振动，渡槽内的流体也会发生晃动，晃动的流体对支撑结构会起减振作用还是会增加结构的振动是一个令人关注的问题。现有的一些研究认为［1-3］，渡槽中的流体具有TLD（调频液体阻尼器）效应，在分析渡槽结构地震反应时，流体不能作为固定质量考虑，当考虑流体晃动效应时，结构的地震反应一般会比流体作为固定质量时要低，因而认为流体的晃动对结构有利，即晃动的流体具有TLD效应。文献［1-3］所论述的流体TLD效应实际上指的是流体晃动的减震效应，现有的流体TLD效应研究都是基于特定的算例得到的计算结论，所得到的某些结论也不尽相同，这些结论是否在一般更为广泛的情况下都适用?有必要做进一步的研究。

渡槽结构工程师需要对槽内流体的晃动效应有充分的理解，才能合理估计结构的地震与或脉动风响应，使得所设计的渡槽结构具有足够的安全储备，如果误认为流体的晃动任何时候都具有减振效应，那将会对结构安全构成不利影响。研究渡槽中流体晃动效应对结构的振动影响，应明确以下二个问题：① 什么是TLD效应?② 什么时候流体对结构振动具有抑制作用?什么时候会具有放大作用?本文将从理论上对以上两个问题展开分析与讨论。

1 什么是TLD效应?

TLD为英文Tuned Liquid Damper的缩写，中文译文为调频液体阻尼器，它实际上是一个盛有液体的容器。TLD本质上是一个动力吸振器，人们可以调节容器内液体的晃动频率使之与结构的基频接近，当结构振动时，TLD能从结构中吸收（并消耗）振动能量，这时TLD中的流体会晃动起来，由于结构的部分振动动能传递给了液体，因而结构的振动幅度会减小，这样就达到结构减振的目的。

由于TLD构造简单、价格低廉，被广泛应用于高层（高耸）建筑的风振控制［4-5］，TLD的设计必须满足二个基本条件：① TLD中的流体晃动频率应调到与结构振动主频率（基频）一致，这可以通过调节流体的断面尺寸来实现；② TLD（子系统）的设计质量应足够小，一般为建筑结构总质量的1% ～2%［4-5］，因为如此小的相对质量对整个建筑结构的主频率（基频）基本没有影响，当TLD被安装在建筑结构上并调频以后，结构的主频率基本保持不变（或者只有细微的变化），这样才能保证TLD的晃动频率与结构主频率一致。实际的TLD通常为浅水型，这时TLD中流体的大多数会晃动起来，流体得到了充分的利用，这样设计的TLD具有较高的效率。

对于渡槽而言，装满水的槽身支撑在结构（混凝土排架、槽墩等）上，看起来很像一个“TLD”，然而这个“TLD”与建筑上所采用的TLD有很大的不同，首先由于渡槽输送水的质量与结构本身的质量相当，有的甚至大于结构本身的质量，当水体的质量加入后，这时结构（包含流体）体系的主频会大幅下降，如果利用渡槽中的水体晃动来达到结构减振的目的，那么必须调节水体的晃动频率与结构主频一致，而这一点实际上很难做到，因为当水体注入渡槽后，结构主频已发生了很大改变；其次渡槽内的水体通常为深水型，这时槽内流体的只有较少的一部分会晃动起来，大多数的流体会像固定质量一样不参与晃动。

2 渡槽流体－结构系统横向动力特性

首先需要对渡槽结构-流体系统进行模态分析才能了解系统的动力特性，从而进一步揭示流体对结构的振动效应。

以下列举四个工程实例，其渡槽结构型式分别为双联排架式、双悬臂式、拱桁架式与斜拉式渡槽（图1～图4）。这些渡槽的结构尺寸与计算取值见文献［6-7］，本文采用ANSYS程序对这四种渡槽结构系统进行建模，建模的方法见文献［8］，流体单元采用Fluid80，槽身结构采用壳单元Shell63，框架结构采用梁单元Beam4，斜拉索采用Link10单元（斜拉渡槽建模与动力特性分析将另文说明）。流体与结构的交界面采用所谓的滑动边界条件，即在交界面上，强制流体与结构的法向位移相等，而两者的切向位移不加以约束。

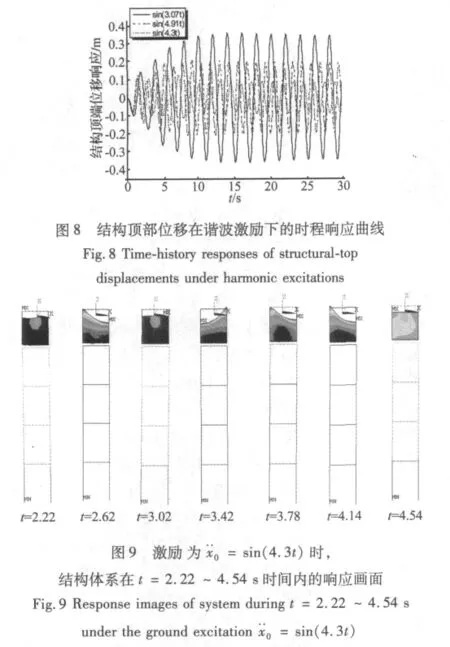
图1为双联排架式渡槽，为了说明问题简单计，仅取了一榀双联排架加以说明；图2为双悬臂式渡槽的一个独立节段；图3为拱桁架式渡槽；图4为斜拉渡槽。其中图1～图3的渡槽在过去均出现过风毁事故［6］。采用Ansys程序对这四种渡槽结构进行空间流-固耦合模态分析，可得到流-固耦合系统一阶与二阶横向振动振型（见图1～图4），它们分别是：① 同相位振型，这时体系的振动频率较低，结构振动的方向与流体的晃动方向一致；② 异相位振型，这时体系的振动频率较高，结构振动的方向与流体的晃动方向相反。

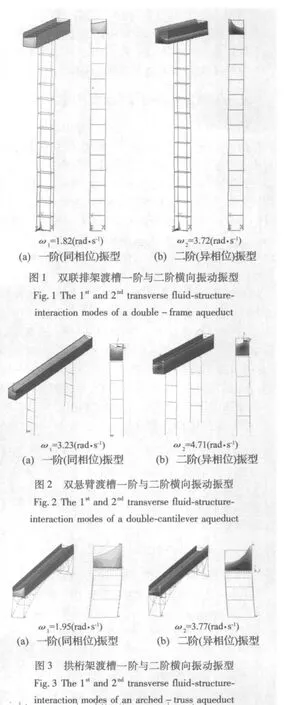
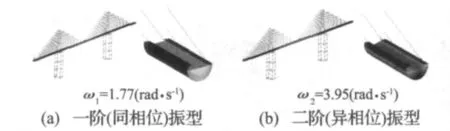
图4 斜拉渡槽一阶与二阶横向振动振型Fig.4 The 1stand 2ndtransverse fluid-structureinteraction modes of a cable-stayed aqueduct

3 流－固耦合作用对横向动力特性的影响

结构-流体系统横向同相位与异相位振型受流体-结构相互耦合的影响，流体-结构相互耦合的强弱取决于支撑结构的刚度与流体质量的多寡，为了展示这种影响，现以文献［7］中的双悬臂渡槽（其横向流-固耦合振型见图2）为例加以说明，排架柱截面为250 mm×400 mm，排架梁截面为250 mm×250 mm，静水截面尺寸为2.05 m×2.0 m，结构跨度为16 m。为了说明问题简单起见，对于图2的双悬臂渡槽，仅通过改变支撑结构刚度来考察流体-结构相互耦合的强弱对体系固有频率的影响，结构的刚度主要取决于结构的布置与截面尺寸，为简单计，这里仅改变支撑结构（双悬臂排架）的弹性模量E来修改结构刚度。设支撑结构的参考弹性模量为E0=3.0×1010（N/m2），取弹性模量E的变化范围为：E=（0.013 ～5.0）E0，采用ANSYS程序，通过空间流-固耦合模态分析，可分别得到系统的一阶（同相位）振动频率ω1、二阶（异相位）振动频率ω2随结构刚度变化的曲线（见图5）。

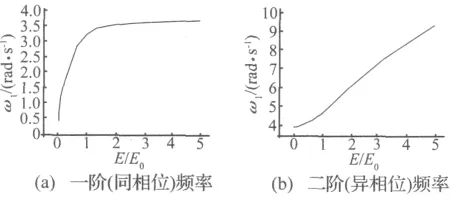
图5 双悬臂渡槽一阶（同相位）频率ω1、二阶（异相位）ω2随结构刚度变化的影响ig.5 Influences of the 1st（in-phase）and 2nd（out-phase）frequencies ω1，ω2due to variation of structural stiffness for a double-cantilever aqueduct

由图5（a）可以看出，当支撑结构刚度较小时，流体-结构的相互作用较为强烈，结构刚度较小的改变会引起流-固耦合系统一阶（同相位）振动频率ω1发生较大的改变；当支撑结构刚度较大时，流体-结构的相互作用较弱，频率ω1随结构刚度改变的影响很小，此时结构的相对振幅很小（几乎不动），体系的振动主要表现为流体的晃动，体系的振动频率ω1趋向于流体的一阶固有晃动频率ωl=3.78（rad/s）。

由图5（b）可以看出，流-固耦合体系的二阶（异相位）振动频率ω2随结构的刚度E近似地呈线性变化。

对于其它结构型式的渡槽，更多的计算分析表明，渡槽流-固耦合作用影响对横向动力特性具有上述（图5）相同的结论，一般的情况是：ω1≤ωl≤ω2。

4 流体的晃动对结构振动的影响分析

4.1 槽内的固定质量、晃动质量效应

为了更好地理解流体晃动的作用，可将渡槽中的流体按等效机械模型［9］考虑。以图6（a）的矩形渡槽为例，则槽内流体可以简化为如图6（b）的固定质量M0与一个质量-弹簧振子（M1，K1）（其中M1为晃动质量，K1为等效的弹簧），质量-弹簧振子对应流体的一阶晃动模态，由于一阶晃动模态在一般动力反应中占有绝对优势地位，因此作为工程应用，一般只需取一阶流体晃动模态即可满足计算精度要求，这里高阶的流体晃动模态忽略不计。图6（b）的模型也通常称之为Housner模型［10］。根据Housner的计算公式，对于不同高宽比的矩形渡槽，表1给出了固定质量M0、晃动质量M1占总质量的份额，表中M为总质量，由表1可以看出，对于常见的高宽比0.6～0.7，槽内固定质量M0占多数，而晃动质量M1占少数，即对于大多数的（矩形）渡槽而言，槽内的水体为深水型，槽内流体的只有较少的一部分会晃动起来，大多数的流体会像固定质量一样不参与晃动。

固定质量与槽体结构同步运动，会加大结构的动力惯性反应。槽内晃动质量M1（子系统）使得结构系统的横向振动模态扩展为如前所述的两个振型：一个为（一阶）同相位振型，另一个为（二阶）异相位振型。流体晃动质量M1在某些情况下对结构能起到减振的作用，对结构安全有利，但在某些情况下则会加剧结构的振动，对结构安全不利。

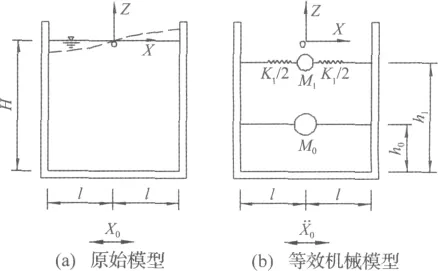
图6 矩形渡槽内流体的等效机械模型Fig.6 Equivalent mechanical model of fluid in rectangular aqueduct

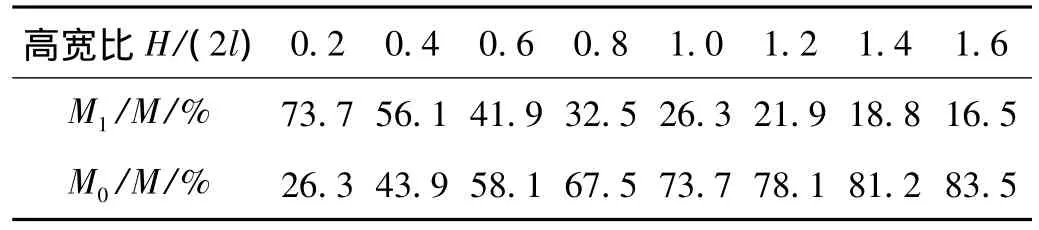
表1 矩形渡槽内不同高宽比下的固定质量M0、晃动质量M1的份额（M为总质量）Tab.1 Percentages of fixed mass M0and sloshing mass M1among total mass with varying aspect ratios for a rectangular aqueduct

4.2 流体对结构的振动效应

渡槽中的流体对支撑结构是否具有减振效应?还是会加剧结构的振动?主要取决于结构系统的幅频响应特性，仍以文献［7］中的双悬臂渡槽为例加以说明，结构阻尼比系数取为5%，取地面加速度脉冲激励为：

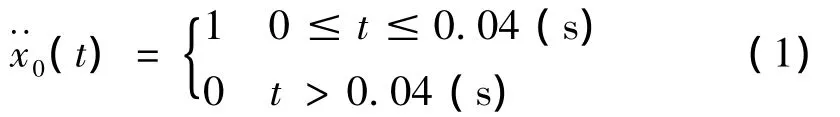
结构刚度按E=3.0×1010（N/m2）（较小）、E=1.5×1011（N/m2）（较大）两种情形考虑，在式（1）的脉冲激励下，首先求解结构顶部位移的脉冲响应，然后对脉冲响应进行Fourier变换可分别得到结构顶部位移的幅频响应曲线见图7。

图7（a）为结构刚度较小的情形，由图可以看出，流体-结构体系出现了两个共振频率，共振峰值对应的频率值为3.07（rad/s），4.91（rad/s），它们正好分别位于结构体系的一阶（同相位）频率ω1=3.23（rad/s）与二阶（异相位）频率ω2=4.71（rad/s）附近。在一阶（同相位）频率ω1处的结构响应幅值较大，而在二阶（异相位）频率ω2处的结构响应幅值较小，在ω3=4.30（rad/s）处，结构响应幅值为极小值。图7（b）为结构刚度较大的情形，由图可以看出，流体-结构体系也出现了两个共振频率，共振峰值对应的频率值为3.68（rad/s），9.20（rad/s），它们正好在结构体系的两个固有振动频率（同相位频率ω1=3.67（rad/s），异相位频率ω2=9.31（rad/s）附近，在第一个固有振动频率ω1处的结构响应幅值较小，而第二个固有振动频率ω2处的结构响应幅值则较大，在ω3=4.30（rad/s）处，结构响应幅值为极小值。

图7（a）、（b）有一个共同的特点，它们均在ω3=4.30（rad/s）处的结构响应取极小值，当再改变结构刚度时，结构响应幅值均在ω3处取极小值，这表明ω3与结构本身无关，ω3仅与槽内的流体截面尺寸有关。

图7 结构顶部位移幅频响应曲线Fig.7 Amplitude-frequency response curves of structural-top displacements

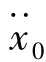
通过以上分析知，只要槽内水体横截面尺寸一定，不论结构如何变化，水体均在频率ω3=4.30（rad/s）处具有减振效应。进一步分析计算表明，其他结构形式的渡槽均具有上述相同的现象，只是ω3的值有所不同而已。

对于一个确定的渡槽流体-结构体系，流体什么时候具有减振效应?什么时候会加剧结构的振动?取决于外动力荷载的频谱特性。对于脉动风作用而言，其卓越频率远低于流体晃动频率，渡槽结构刚度愈小，结构的脉动风响应愈大，这时流体-结构相互作用愈强烈，结构体系的一阶横向同相位振动频率处于较低的位置，同相位模态在脉动风响应中起到主要作用，这时流体晃动与结构的振动方向一致，流体的晃动会加剧结构的振动，对结构会起不利的作用；当渡槽结构刚度较大时，结构的脉动风响应很小，通常可以忽略不计。对于地震作用而言，当场地的卓越频率与ω1（或ω2）接近时，结构会发生共振反应，流体的晃动会加剧结构的振动，但当场地的卓越频率与ω3接近时，流体才具有减振作用（所谓的TLD效应），结构反应较小。根据图7的位移幅频响应曲线可以看出，当动力荷载的频率很小或很大时，结构体系的动力反应很小。

另外需要指出的是，本文所讨论的流体的晃动都，程，系统的固有频率ω1，ω2与流体、结构的振幅无关，现有的研究表明［11］：当流体晃动幅度较大时，流体的运动呈现非线性，系统的固有频率随流体振幅发生变化。对于TLD而言，当流体晃动幅度较大时，流体调频效应被打破，其减振效应会大打折扣，因此水体晃动的幅度越大，TLD减振效应未必越大。

5 结论

（1）渡槽体系的横向模态都呈现两个基本形态：一阶（同相位）振型，这时体系的振动频率ω1较低，支撑结构振动的方向与流体的晃动方向一致；二阶（异相位）振型，这时体系的振动频率ω2较高，支撑结构振动的方向与流体的晃动方向相反。

（2）渡槽内的流体质量可以分为固定质量与晃动质量两部分，其中流体中的固定质量与槽体结构同步运动，会加大支撑结构的动力惯性反应，可能会对结构安全不利。

（3）当外动力荷载的卓越频率与ω1（或ω2）接近时，结构体系会发生共振反应，晃动的流体会加剧支撑结构的振动。

（4）当外动力荷载的卓越频率与ω3接近时，晃动的流体对支撑结构起到减震的作用。

为什么渡槽内的流体在固定的频率ω3处具有减振效应，并且ω3不随结构的改变而改变，其内在物理机制需要作进一步的研究。目前渡槽的设计，由于考虑温度等的影响，槽体与墩体间通常采用施加盆式支座或其他的柔性连接，关于盆式支座或其他的柔性连接对渡槽结构流—固耦合振动的影响需要作进一步的研究。

［1］张俊发，刘云贺，王 颖，等.渡槽-水体系统的地震反应分析［J］.西安理工大学学报，1999，15（4）：46-51.

［2］吴 轶，莫海鸿，杨 春.三维排架渡槽中水的调频液体阻尼效应［J］.水利学报，2005（9）：1115-1120.

［3］季日臣，夏修身，陈尧隆，等.考虑流一固藕合梁式矩形渡槽横向地震响应研究［J］.地震学报，2007，29（3）：328-333.

［4］Wakahara T，Ohyama T，Fujii K.Suppression of wind-induced vibration of a tall building using tuned liquid damper［J］.Journal of Wind Engineering and Industrial Aerodynamics，1992，43（1-3）：1895-1906.

［5］Sun L M，Fujino Y，Pacheco B M，et al.Modeling of turned liquid damper［J］. JournalofWind Engineeringand Industrial Aerodynamics，1992，41（44）：1883-1894.

［6］ Li Y C，Luo L R.Wind-destroyed mechanism analyses of three aqueductbridges［C］.Proceedingsofthe 12th International Conference on Wind Engineering， Cairns，Australia，2007：1535-1542.

［7］李遇春.某双悬臂渡槽风致破坏原因分析［J］.同济大学学报，2008，36（11）：1485-1489.

［8］李遇春，楼梦麟，尚 伟，等.大型渡槽抗震分析中流体的位移有限元模式［J］.水利学报，2003（2）：93-97.

［9］Ibrahim R A. Liquid sloshingdynamics（theoryand applications）［M］.Cambridge University Press，2005.

［10］ Housner G W.Dynamic pressure on accelerated containers［J］.Bulletin of the Seismological Society of America，1957，47（1）：15-35.

［11］ Ikeda T，Nakayama N.Nonlinear vibration of a structures caused by water sloshing in a rectangular tank［J］.Journal of Sound and Vibration，1997，201（1）：23-41.