基于柔性多体动力学的瓦楞成型系统建模与仿真研究

曹大志 ， 赵治华 ， 强洪夫 ， 任革学

（1.清华大学 工程力学系，北京 100084；2.第二炮兵工程大学 201室，西安 710025）

在一些如传送机械、太阳能帆板伸展机构、机械臂等系统中，柔性体的变形对系统的动力学行为产生很大的影响，传统的多刚体系统动力学理论已经不能满足人们对设备越来越高的精度要求。此外随着材料技术和制造技术的进步，越来越多的柔性部件应用到存在大位移和大变形的系统中。于是，柔性体的大变形多体动力学问题不断出现，传统的基于小变形理论建立动力学模型的方法已不能得到这类大变形柔性多体动力学问题的精确解。Shabana［1-2］提出的绝对节点坐标法可以很好的解决这类大变形柔性多体动力学问题，并且在多体动力学领域受到广泛的重视。不同于传统的浮动坐标系法，共旋坐标法或相对节点位移法等，基于绝对节点坐标的单元节点的广义坐标直接采用的是空间坐标及其梯度，因此在解决众多动力学问题中具有很大优势。绝对节点坐标法的出现促进了柔性多体动力学与有限元理论的进一步整合，基于绝对节点坐标法的梁［3］，板/壳［4］和三维实体［5］等单元陆续的提出。在我国对绝对节点坐标法的研究起步较晚。刘锦阳等［6-11］基于绝对节点坐标做了以下工作：考虑了热载荷与结构变形的耦合，分析了复合材料以及柔性板的多体系统动力学；提出一套混合坐标体系，采用绝对节点坐标法进行了验证；此外还考虑了材料的弹塑性，求解了梁的刚柔耦合动力学特性。张云清等［12-14］基于绝对节点坐标法研究了含分数阶阻尼特性元件的多体系统建模和求解问题，并针对约束方程的违约问题提出高效的数值计算方法。蔡逢春等［15］基于绝对节点坐标法建立了一种新的一维二节点输流管道单元，计算和分析了不同边界条件下的输流管道的非线性动力学行为。

在金属冶炼或印刷等轧制工业的加工和处理流程中，带材会自行偏离生产线的中心，向辊子的一边移动，这称为带材跑偏。国外众多学者对轧制过程的出现的带材跑偏的动力学行为进行了研究。Shelton等［16］基于欧拉梁假设推导得到了带材横向位移的数学模型。Laukkanen［17］提出四节点的 Mindlin-Reissner弯曲板单元，并对带纸进行了静力学和动力学分析。Kulachenko等［18］基于混合坐标法提出四节点20自由度的壳单元，采用缩减积分的办法克服了剪切锁死的问题。Yu等［19］对带钢的跑偏纠偏装置进行了多体动力学仿真，此外还有学者对带材的跑偏行为和纠偏装置进行了实验研究［20］。

大型复杂结构本身受诸多因素的限制，其实验往往很难进行，因此有必要借助先进的仿真手段来得到较精确的系统模型。现代柔性多体动力学理论特别是绝对节点坐标法的发展为复杂多体系统的建模和仿真提供了有利的工具。本文借助现代柔性多体动力学理论，以某型号瓦楞机的瓦楞成型系统为对象，建立了系统的柔性多体动力学仿真模型，并对传送带的跑偏等动力学行为进行了分析。

1 柔性多体动力学理论

本节简要介绍基于绝对节点坐标壳单元的有限元格式，赫兹碰撞理论和柔性多体系统方程的求解。

1.1 绝对节点坐标的壳单元描述

Dufva等［14］基于绝对节点坐标体系提出了一种可精确描述任意刚体位移和大变形的四节点36自由度的壳单元。如图1所示。其中a、b和t分别为板壳单元的长度、宽度和高度。

图1 基于绝对节点坐标的四节点壳单元Fig.1 The ANC-based four nodes shell element

此单元含有四个节点，单元的广义坐标表示为：

其中ei为第i个节点的广义坐标，包含有空间位置向量ri及其在中性面上两个方向的一阶导数和，故每个节点共有9个自由度：

单元中任一点的绝对坐标r可表示为单元节点坐标e的有限元插值形式：

其中：ξ为实体单元母单元的自然坐标，N为单元的形函数［4］。单元的动能可表示为：

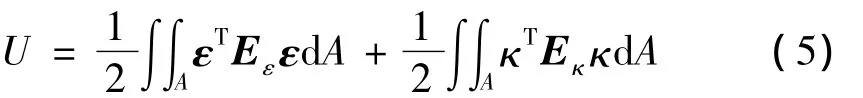
其中：ε和κ分别为壳单元面内的膜应变和横向曲率，具体定义见文献［4］。Eε，Eκ分别为壳单元的弹性矩阵，并且能够描述材料的正交各向异性。

基于虚功原理，无约束的单元的动力学方程可表达为：

式中：Fe为单元弹性力列阵，Qe为广义外力列阵。

1.2 碰撞检测和赫兹碰撞理论

接触碰撞分析是机械动力学的重要环节，很多情况下，机械中各零件之间力的传递是通过两零件的接触碰撞来实现的。在瓦楞机工作过程中，柔性的传送带和刚性的各支撑辊之间存在大面积的接触碰撞，因此需要采用合理、高效的接触算法对其进行建模。

本文采用在单元内布置若干检测点的方法，将柔性传送带与刚体支撑辊侧面的面-面之间的碰撞检测简化为点-面之间的检测，如图2所示。

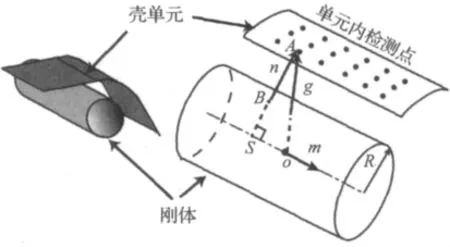
图2 壳单元与刚体的碰撞Fig.2 The shell-to-rigid contact

由赫兹理论可得碰撞点上的摩擦碰撞力f为：

其中n为碰撞点的法线方向，如图2所示。fn、fτ和τ分别为法向碰撞力、摩擦力和切向单位向量，其具体计算公式见文献［21］。

利用虚功原理，作用在检测点p处的碰撞摩擦力fp可以转化为单元广义节点力Qp：

其中N是单元的形函数。

1.3 基于绝对节点坐标的柔性多体系统动力学方程及求解

基于绝对节点坐标柔性体的总动能和总势能可由单元动能式（4）和势能式（5）累加而成：

其中n和ne分别代表节点个数和绝对节点坐标单元的个数。利用第一类Lagrange方程，可得到含约束的基于绝对节点坐标的多体系统动力学方程为：

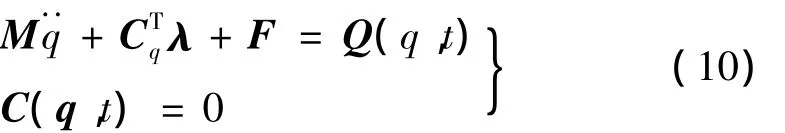
式中：q为柔性的广义坐标；λ为拉格郎日乘子列阵；C（q，t）为约束方程；Cq为约束方程对q的偏导数矩阵；M为柔性体的质量阵；Q为广义外力列阵；F为柔性体的弹性力列阵，是柔性体总势能对q的偏导数：

式（10）是一组典型的微分代数方程组（DAEs），可由隐式的向后差分法［12］（Backward Differentiation Formulas，BDF）求解。

2 瓦楞成型系统的多体动力学建模

瓦楞机是生产瓦楞纸板的机构，它是由传送带，张力辊，上下瓦楞辊等部件组成（见图3）。瓦楞机的基本工作原理：经预热和预湿后的瓦楞原纸（纸2）进入上下瓦楞辊的通道受挤压熨烫成型为瓦楞芯纸。由涂胶辊上胶后随瓦楞辊继续运转，与同时经过预热及温控后到达的面纸1在绷紧的传送带的压力作用下进行热压复合干燥，由此高速运转，生产出二层瓦楞纸板。

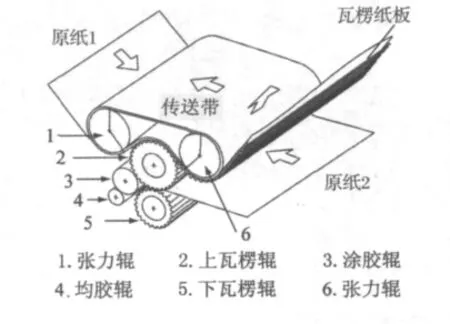
图3 瓦楞机Fig.3 The corrugating machine

如果两个旋转张力辊由于生产或是安装误差导致不平行，或是辊子转动的方向与传送带运行的方向不垂直，就会造成原纸跟随传送带的跑偏、瓦楞芯纸与面纸未对齐、纸板的各种翘曲等各种影响生产的异常现象。因此有必要掌握瓦楞机的动力学行为。

2.1 瓦楞成型系统的尺寸及仿真模型

瓦楞成型系统是瓦楞机的核心，主要是由传送带与三个支撑辊（两个张力辊和上瓦楞辊）组成，模型如图4所示。其中将传送带考虑成柔性体，将支撑辊考虑成刚体，在本文中将瓦楞辊考虑成表面光滑的圆柱体，不考虑瓦楞辊的锯齿。模型参数见表1，其中碰撞相关参数由赫兹碰撞理论通过实验而得到。

图4 瓦楞成型系统Fig.4 Modeling image of corrugating machine

表1 模型参数Tab.1 Model＇s parameters

采用1.1节中所描述的基于绝对节点坐标法的36自由度的壳单元对传送带进行有限元离散，如图5所示。值得注意的是基于绝对节点坐标单元的位移模式相对传统的有限元含有更高阶的完备多项式，因此网格划分的可以相对稀疏。经收敛性测试实验，将传送带划分为40×1的网格密度可保证数值解的收敛。

传送带与三个支撑辊的碰撞采用1.2节所述的点-面检测的办法进行建模。由于基于绝对节点坐标的单元的网格密度相对稀疏，因此在每个板壳单元内部布置7×7=49个检测点，考虑到每个检测点需要和三个支撑辊的圆柱表面进行点-面碰撞检测，因此在模型中共建立49×40×3=5 880个点-面碰撞检测对。

图5 传送带的有限元模型Fig.5 FEM model of resin belt

2.2 瓦楞机工况的边界条件

边界条件主要包含有运动约束和载荷，其中运动约束如图4所示，载荷边界条件如图6所示。

图6 载荷边界条件Fig.6 The load boundary condition

3 仿真结果分析

采用自主研发的多体动力学程序对瓦楞成型系统的仿真模型进行动力学分析，仿真时间取为15 s。采用基于浮动坐标系（floating frame of reference formulation，FFRF）的小变形的壳单元建立相同的动力学模型，并进行对比分析。值得注意的是，由于基于小变形的壳不能较准确的求解大变形的问题，因此本文采用基于FFRF的小变形单元的网格更加精细。

从瓦楞机的工况可知，由于编号为2的张力辊两端所受力大小不同，因此它与编号为1的张力辊不再平行，从而导致了传送带受力不均，发生跑遍。基于ANCF和FFRF两种不同建模方法下，得到编号为2的张力辊沿X方向的位移和传送带中心（见图5）沿Z方向的偏心位移，如图7和图8所示。从两图的对比可知，计算结果基本一致，从而也验证了基于绝对节点坐标建模方法的准确性。此外，采用基于绝对节点坐标的建模方法，需要的单元个数少，相对浮动坐标系下的小变形单元建模的方法，本文中基于绝对节点坐标系的建模方法具有更高的计算效率和计算精度。

在瓦楞机的工作过程中，瓦楞芯纸与面纸的粘合是通过上瓦楞辊与传送带的接触碰撞实现的。适合的碰撞力可以在不压碎瓦楞芯纸的情况下，让面纸与瓦楞更充分的粘合。利用传送带上的检测点与圆柱侧面的解析检测方法，能准确描述带与支撑辊之间的面与面的摩擦碰撞，从而较准确的模拟瓦楞机在压制过程中的工作状态。计算得到的摩擦碰撞力分布如图9所示。

在瓦楞机的工作过程中，研究传送带的最大Mises应力或最大主应力等，可以分析传送带的强度是否满足要求，并且传送带的应力分布规律也是进行其疲劳分析的基础。图10为带中心Mises应力的时间历程曲线，图11为传送带在稳定工作过程的应力分布图。从图11可知由于编号为2的张力辊两端受力不均，因此导致带的应力分布同样不均。在受力较大一端的应力明显比受力小的一端大。带的内部应变分布的不均也直接导致带子朝张力小的方向移动。

图9 碰撞力显示Fig.9 The display of contact force

图12（a）～（e）显示的是传送带的变形历程，在t=0 s时，传送带处于未变形的构型，是一个圆柱壳。在t=0～1 s时间段，由于受张力辊的拉伸以及上瓦楞辊的挤压开始绷紧，然后在逐渐增大的张力的作用下发生弹性变形，随后受瓦楞辊摩擦接触力驱动传送带开始旋转，如图12（d）和（e）中所示。图12（f）为传送带中心点在三维空间中的运动轨迹图，可明显看出传送带经历了大位移、大转动的运动过程。

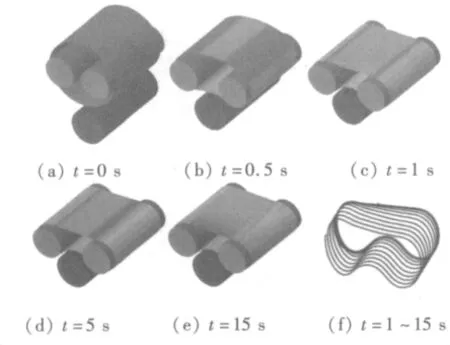
图12 传送带变形历程Fig.12 Snapshots of resin belt animation

对机械的动力学行为分析最终的目的是对系统进行动力学控制。由于现代造纸以及轧制过程的控制非常复杂，设计到速度、张力、压力等大量物理参数，以及结构的变形及部件之间的摩擦碰撞，因此是一个非线性、强耦合的复杂过程。基于绝对节点坐标的建模方法，可以研究不同边界条件下如施加的张力，带材的驱动速度等对带材的动力学行为的影响。此外还可方便地获得如偏移量，碰撞力，应力分布等动力学响应参数，为下一步的动力学控制打下基础，为控制参数的选择和优化提供依据。

4 结论

瓦楞机轧制纸板的过程是个非线性、强耦合的复杂过程，本文采用基于绝对节点坐标的板壳单元离散传送带，既精确地描述了传送带的大转动和大位移的刚体运动，又描述了传送带的非线性变形。采用点-面检测的方法和赫兹碰撞理论描述了支撑辊与传送带之间的大面积接触碰撞、强耦合变形的动力学行为。在自主研发的多体动力学程序中计算得到柔性和刚性部件的动位移，碰撞力大小以及应力分布等动响应，为进一步的动力学控制和系统的设计和改进提供了理论的基础。综上，基于绝对节点坐标的建模方法在处理柔性多体大变形动力学问题具有很大的潜力。

［1］ Shabana A A.Flexible multibody dynamics：review of past and recent developments［J］.Multibody System Dynamics，1997，1（2）：189-222.

［2］Shabana A A.Definition of the slopes and the finite element absolute nodal coordinate formulation［J］.Multibody System Dynamics，1997，1（3）：339-348.

［3］Shabana A A，Yakoub R Y.Three dimensional absolute nodal coordinate formulation for beam elements：theory［J］.Journal of Mechanical Design，2001，123（4）：606-613.

［4］Dufva K，Shabana A A.Analysis of thin plate structures using the absolute nodal coordinate formulation［J］.Proceedings of the Institution of Mechanical Engineers Part K-Journal of Multi-Body Dynamics，2005，219（4）：345-355.

［5］ Gerstmayr J，Schoberl J.A 3D finite element method for flexible multibody systems［J］.Multibody System Dynamics，2006，15（4）：309-324.

［6］Liu J Y，Lu H.Thermal effect on the deformation of a flexible beam with large kinematical driven overall motions［J］.European Journal of Mechanics-A/Solids，2006，26（1）：137-151.

［7］ Liu J Y，Lu H.Rigid-flexible coupling dynamics of threedimensional hub-beamssystem［J］. MultibodySystem Dynamics，2007，18（4）：487-510.

［8］ Liu J Y，Hong J Z.Nonlinear formulation for flexible multibody system with large deformation［J］.Acta Mechanica Sinica，2007，23（1）：111-119.

［9］石 望，刘锦阳.大变形弹塑性梁的刚-柔耦合动力学特性［J］.上海交通大学学报，2011，45（10）：1469-1474.

SHI Wang， LIU Jin-yang. Investigation on rigid-flexible coupling dynamics for elasto-plastic beam with large deformation［J］.Journal of Shanghai Jiaotong University，2011，45（10）：1469-1474.

［10］ Liu J Y，Hong J Z，Cui L.An exact nonlinear hybridcoordinate formulation for flexible multibody systems［J］.Acta Mechanica Sinica，2007，23（6）：699-706.

［11］Liu Z Y，Hong J Z，Liu J Y.Finite element formulation for dynamics of planar flexible multi-beam system［J］.Multibody System Dynamics，2009，22（1）：1-26.

［12］ Zhang Y Q，Tian Q，Chen L P，et al.Simulation of a viscoelastic flexible multibody system using absolute nodal coordinate and fractional derivative methods［J］.Multibody System Dynamics，2009，21（3）：281-303.

［13］田 强，张云清，陈立平，等.含分数阻尼特性元件的多体系统动力学研究［J］.力学学报，2009，41（6）：920-928.

TIAN Qiang，ZHANG Yun-qing，CHEN Li-ping，et al.Dynamics research on the multibody system with fractional derivative damper［J］.Chinese Journal of Theoretical and Applied Mechanics，2009，41（6）：920-928.

［14］ Tian Q，Chen L P，Zhang Y Q，et al.An efficient hybrid method for multibody dynamics simulation based on absolute nodal coordinate formulation［J］.Journal of Computational and Nonlinear Dynamics，2009，4（2）：021009-021014.

［15］蔡逢春，臧峰刚，叶献辉，等.基于绝对节点坐标法的输流管道非线性动力学分析［J］.振动与冲击，2011，30（6）：143-146.

CAI Feng-chun，ZANG Feng-gang，YE Xian-hui，et al.Analysis of nonlinear dynamic behavior of pipe conveying fluid based on absolute nodal coordinate formulation［J］.Journal of Vibration and Shock，2011，30（6）：143-146.

［16］ Shelton J J，Reid K N.Lateral dynamics of a real moving web［J］.ASME J.Dyn.Syst.Meas.Control，1971，93（3）：180-186.

［17］ Laukkanen J.Fem analysis of a travelling web［J］.Computers＆ Structures，2002，80（24）：1827-1842.

［18］ Kulachenko A，Gradin P，Koivurova H.Modelling the dynamical behaviour of a paper web.part I［J］.Computers＆ Structures，2007，85（3-4）：131-147.

［19］ Yu L，Zhao Z，Ren G.Multibody dynamic model of web guiding system with moving web［J］.Journal of Dynamic Systems， Measurement， and Control， 2010， 132（5）：051004-051010.

［20］ Ryu J K，Lee S G，Rhim S S，et al.Simulation and experimental methods for media transport system：PartⅡ，effect of normal force on slippage of paper［J］.Journal of Mechanical Science and Technology，2005，19（1）：403-410.

［21］虞 磊，赵治华，任启鸿，等.基于绝对节点坐标的柔性体碰撞仿真［J］.清华大学学报（自然科学版），2010，50（7）：1135-1140.

YU Lei，ZHAO Zhi-hua，REN Qi-hong， et al. Contact simulations offlexiblebodiesbased on absolute nodal coordinates［J］.Journal of Tsinghua University（Science and Technology），2010，50（7）：1135-1140.

［22］ Hairer E，Wanner G.Solving ordinary differential equationsⅡ：stiff and differential-algebraic problems ［M］.Heidelberg：Springer-Verlag，1996.