非饱和地基中Love波的传播特性

陈炜昀， 夏唐代， 王志凯， 孙苗苗

（1.浙江大学 软弱土与环境土工教育部重点实验室，杭州 310058；2.浙江大学 岩土工程研究所，杭州 310058；3.浙江万科南都房地产有限公司，杭州 310058；4.浙江省水利河口研究院，杭州 310027）

表面波的传播在土木工程、地震工程和地球物理学等许多领域都有着重要的实际意义，并受到广泛地关注。目前，应用较广泛的表面波无损检测方法（SASW法）就是利用面波（如Rayleigh波和Love波）的弥散特性通过分析现场测试结果来反演土层参数（如土层剪切波速度等）的一种方法。此外，在地震工程中，Love波动理论成功地揭示了地震记录中出现的频散波现象［1］。理想弹性介质中Love波的传播机理已得到完善的研究［2，3］，但是这些研究将各类地基弹性化处理，实际应用的合理性还有待证实。随后，越来越多的学者［4-7］将土体视为由一种饱和流体多孔弹性固体所组成的多孔介质。Deresiewicz［4］首先应用 Biot［5］的经典模型研究了这种多孔介质层中的Love波，建立了关于频率和相速度的多孔介质中的Love波的弥散方程。夏唐代［6］运用有限元法推导出饱和土中Love面波的弥散特性方程，并且讨论了饱和土中Love面波波速度的弥散特性及位移分布规律。夏唐代［6］根据Love波的传播特性提出了一种有效地基动力响应计算方法。Wang等［7］利用迭代法求解了横观各向同性的饱和多孔介质中Love波的频散方程，并给出了Love波的弥散曲线和衰减曲线。文献［8］运用解析法建立了交通荷载作用下双层地基中Love波的特征方程，并分析了不同情况下Love波的弥散性和位移分布特征。

上述研究主要是针对地基土或岩石孔隙中只包含一种成分（水、气或油）的情形。然而实际上，地球表面绝大部分覆盖的岩石或土的孔隙中同时包含有两种或两种以上不同的流体，如水，气体和油，使得其土体动力特性也会有明显的变化，因此，对非饱和土中Love波弥散特性研究更有实际意义。但是至今很少有涉及到针对饱和度对多孔介质中Love波的影响的研究，这使得本文的研究具有更大的现实意义。

本文研究了非饱和土中Love波的传播特性，得到了相应的弥散方程，首先分析了饱和度对非饱和地基土层中剪切波传播的影响，然后利用文献［7］中的迭代法求解了该方程并得到了不同模态Love波的频散和衰减曲线，分析了地基土体饱和度、频率与Love波传播波速、衰减系数的关系，最后讨论了饱和度变化对Love波的水平位移分布特征的影响。

1 问题描述

现考虑一个厚度为H，覆盖在一个各向同性、均匀的半无限弹性体上的非饱和土层中Love波的传播。建立的笛卡尔坐标系如图1所示，其中x-y平面在非饱和多孔介质层与弹性体之间的水平分界面上，z轴垂直向下指向半空间。

图1 Love波传播示意图Fig.1 Geometry of the Love wave problem

Wei等［9-10］建立了非饱和多孔介质的本构关系和基本波动方程：

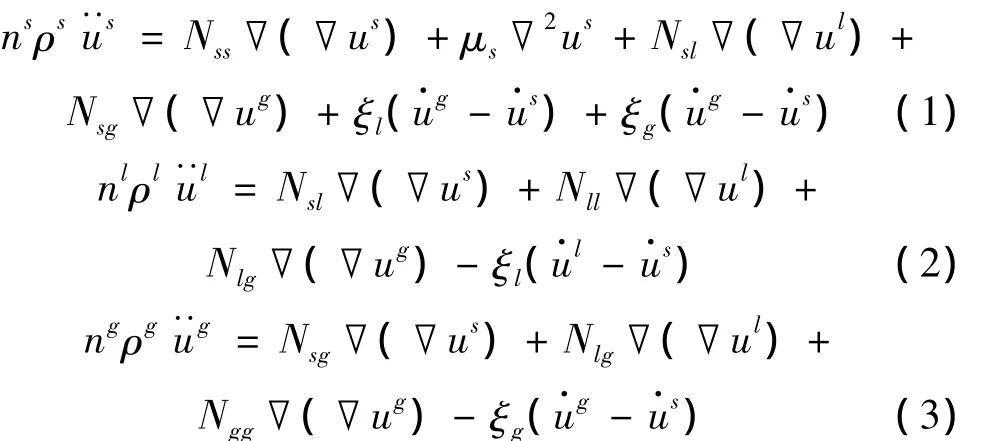
式中：Nss，Nsl，Nsg，Nll，Nlg，Ngg为独立参量［9］；μs为土骨架的宏观拉梅常数；ns，nl，ng分别为固体骨架、水、空气的体积分数；ρs，ρl，ρg分别为三相的密度；ξl和ξg分别为流体和气体的耦合作用参数，Garg［11-12］等提出以下关系式：

式中：ηl和ηg为流体粘度；k为该多孔介质的绝对渗透率；和分别为液体和气体的相对渗透率；Van［13］给出了目前应用较广的VG模型，描述了相对渗透率与饱和度Sr关系式：

式中：m称为VG模型参数。

2 非饱和土层中的场方程

对于本文考虑的反平面剪切运动，只y方向有非零位移分量uy和，以下推导中用上标*表示对应上覆土层的物理量。令固相、气相、液相的位移为简谐时间变化，则：

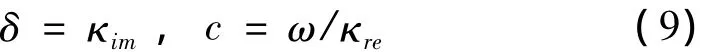
将式 （8）代入式（1）～式（3），得：

其中，γ2=κ2-，且：

从式 （10）～式 （13）可以看出，一方面，复数κ表明非饱和多孔介质层中的Love波是耗散的；另一方面，液相和气相的位移和土骨架的位移是相互耦合的。解二阶偏导方程 （10）可得到非饱和土层中的波场如下：

其中，A1和A2为常数，γ*2=κ*2-。

当z＞0，下覆弹性半空间的位移沿y方向分量可表示为：

3 边界条件和弥散方程

对于本文所讨论的问题，假设上覆非饱和多孔介质层与下部弹性体之间的接触良好。当z=0时，接触平面上应力和位移连续，假设孔隙中的水和气体不能透过接触面。可以得到以下的边界条件：

由边界条件得：

要使上式中A1，A2，A3有非零解，则其系数行列式必须为零，因此可以得到Love波的弥散方程：

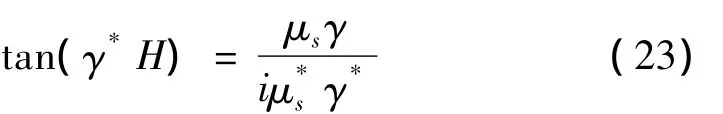
弥散方程（23）是一个复数形式的超越方程，无法获得解析解，通常只有数值解或近似解。现通过分离其实部和虚部可由如下2个实方程代替：

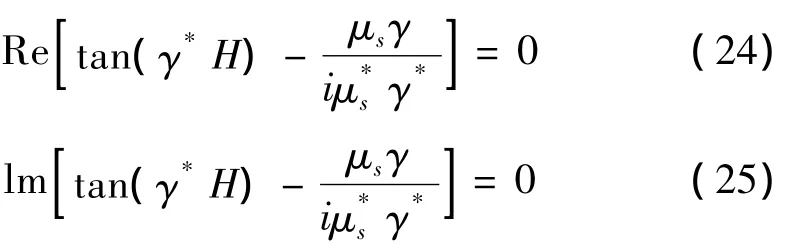
因为已知波的衰减系数很小 （δ≪1），利用文献［7］中的迭代方法求解。

另外，根据式 （20）～式（22），再结合式 （14）、式（15），可以得到上下两种介质的水平位移分别为：

波在传播过程必须要耗散，因此Love波的波场公式（15）中γ的虚部必须大于零，另外，这里假设Re（γ*）＞0，可得Love波的波速范围如下：

其中，非饱和土层和下部弹性半空间中的剪切波速和cs可分别表示为：

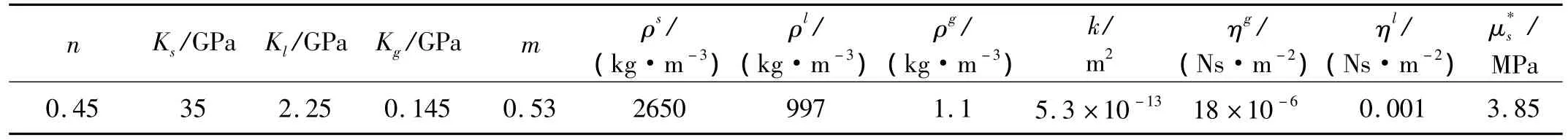
表1 非饱和土的基本参数［14］Tab.1 Basic parameters of unsaturated soil

4 数值分析

本文首先考虑无限空间内非饱和孔隙介质中剪切波的传播并谈论饱和度及频率对剪切波速的影响。算例中孔隙介质物理常数取自Columbia非饱和砂土［14］，如表1。考虑的频率范围从1～107Hz，涵盖了土木工程，地球物理学，及地震工程中可能遇到的频率范围［15］。然后分析在低频率条件下，非饱和土中Love波的传播特性。考虑一个厚度为10 m的非饱和土层覆盖在一个弹性半空间上。非饱和土层物理常数同样取自Columbia非饱和砂土［14］，如表1。假设下部弹性半空间的密度与上部土层中固相介质的密度相同，拉梅常数μs=9 MPa。故下部半空间中剪切波速cs=58.28 m/s。通过数值计算得到了Love波的弥散曲线及其他相关曲线。

4.1 饱和度对剪切波速的影响

图2表示在不同的频率下剪切波速随着饱和度的变化趋势。所考虑的饱和度变化范围为0.01～0.99。可以看出在频率较低时（ω＜106Hz），剪切波速随着饱和度的增加而减小。另外，结果显示，当频率较低时，频率变化对剪切波波速影响很小。图3表示在不同的饱和度条件下剪切波速随着频率的变化趋势。所考虑的频率变化范围为1～107Hz。可以看出，当频率较低时，频率对剪切波速的影响很小，当频率较高时，不同饱和度下的剪切波速将随着频率增加而增加。饱和度越高，土层中Love波波速开始增加所需要的频率越低。

图2 不同饱和度时的剪切波速Fig.2 Velocity of shear waves with different saturation

图3 不同饱和度时的剪切波速Fig.3 Velocity of shear waves with different frequency

4.2 饱和度对LOVE波相速度和衰减的影响

图4给出了第n阶模态波（n=1，2，3）对应不同饱和度时的相速度曲线。在频率较低时，地基中的Love波的波速与下部介质中的剪切波速接近；当频率较高时，则趋近于上层地基中的剪切波速。从图4可以看出，各种模态的Love波在不同饱和度条件下的波速都是随着频率增加而减小的。饱和度越高，Love波波速越低。这是由于Love波是由上下不同介质中的剪切波SH波干涉产生的。当饱和度升高时，上部土层中剪切波速减小，所干涉产生的Love波波速也随之降低。从图4看出，在频率较低时，波速减小较快，当频率较高时，波速趋于缓慢。当饱和度不同时，第1模态的Love波的截止频率都等于0 Hz。但是从图4看出，当饱和度分别为：0.2，0.4，0.6，0.8 和 0.99 时，第 2 模态波的截止频率值分别为：31 Hz，28 Hz，26 Hz，24 Hz 和23 Hz；第2模态波的截止频率值分别为：61 Hz，58 Hz，51 Hz，48 Hz和45 Hz。因此，高模态 （n≥2）的 Love波的截止频率值和饱和度有关，饱和度越高，截止频率越低。

图5出了对应不同饱和度时Love波的衰减曲线。从图中可以看出，三种模态的Love波的衰减在不同饱和度条件下，都是随着频率的增加先迅速增加而后趋于缓慢。而且饱和度越高，波衰减越快。

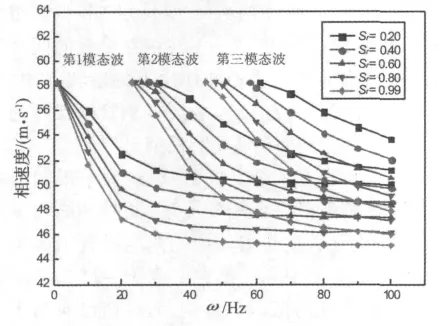
图4 不同饱和度时的Love波的频散曲线Fig.4 Dispersion curve of Love waves with different saturation

图5 不同饱和度时的Love波的衰减曲线Fig.5 Attenuation curve of Love waves with different saturation

4.3 饱和度对LOVE波水平位移分布的影响

图6和图7分别给出了频率分别为10 Hz和40 Hz时不同饱和度时的第1阶和第2阶模态波水平位移分布曲线。图中位移幅值均采用了无量纲化。可以看出Love波的最大位移总是出现在自由表面上。对于下部弹性半空间（z≤0）而言，饱和度的变化对其水平位移分布影响较为显著。饱和度越高，水平位移幅值减小越快，相应的位移影响深度越小。另外，从图中可以看出，高阶模态波的水平位移较低阶模态波衰减更快，其位移影响深度也越小。

5 结论

本文运用解析法建立了非饱和土层中Love波的弥散特征方程和位移方程，并利用迭代法对弥散方程和位移方程进行了数值计算分析。数值计算结果表明，在实际工程中关注的频域范围内（ω≤106Hz），地基中的剪切波速不受频率变化影响，且随饱和度增加而逐渐减少。

此外，算例结果表明饱和度对土层中Love波的波速、衰减和水平位移分布影响较为显著。高阶模态（n≥2）Love波的截止频率和饱和度有关，饱和度越高，截止频率越低。实际地震波的频率较小，主要为第1阶模态的Love波。本文理论为分析实际工程提供了理论依据，有一定的实际应用价值。

［1］黎在良，刘殿魁.固体中的波［M］.北京：科学出版社，1995.

［2］Ewing W M，Jardetzky W S.Elastic waves in layered media［M］.London：McGraw-Hill Book Company（UK）Limited，1957.

［3］夏唐代.地基中表面波特性及应用［D］.杭州：浙江大学，1992.

［4］Deresiewicz H.The effect of boundaries on wave propagation in a liquid filled porous solid：II.Love waves in a porous layer［J］.Bulletin of the Seismological Society of America，1961，51（1）：51-59.

［5］Biot M A.Theory of propagation of elastic waves in a fluidsaturated porous solid：I.Love frequency range［J］.The Journal of the Acoustical Society of America，1956，28（2）：168-178.

［6］夏唐代，王立忠，吴世明.饱和土中Love波弥散特性［J］.振动工程学报，1994，7（4）：357-362.

［7］ Wang Y S，Zhang Z M.Propagation of love waves in a transversely isotropic fluid-saturated porous layered half-space［J］.The Journal of the Acoustical Society of American，1998，103（2）：695-701.

［8］颜可珍，夏唐代.交通荷载作用下地基中Love波的传播特性［J］.岩土力学，2005，26（7）：1118-1122.

［9］ Wei C，Muraleetharan K K.A continuum theory of porous media saturated by multiple immiscible fluids：I.linear poroelasticity［J］.International Journal of Engineering Science，2002，40（16）：1807-1833.

［10］ Wei C，Muraleetharan K K.A continuum theory of porous media saturated by multiple immiscible fluids：II.lagrangian description and variationalstructure［J］. International Journal of Engineering Science，2002，40（16）：1835-1854.

［11］ Garg S K，Nayfeh A H.Compressional wave propagation in liquid and or gas saturated porous media［J］.Journal of Applied Physics，1986，60（9）：3045-3055.

［12］ Berryman J G，Thigpen L，Chin R C Y.Bulk elastic wave propagation in partially saturated porous solids［J］.Journal of the Acoustical Society of America，1988，84（1）：360-373.

［13］ Van G M T.A closed-form equation for predicting the hydraulic conductivity of unsaturated soils［J］.Soil Science Society of America Journal，1980，44（5）：892-898.

［14］ Lo W C，Sposito G，Majer E.Wave propagation through elastic porous media containing two immiscible fluids［J］.Water Resources Research，2005，41（2）：1-20.

［15］ Murphy W F.Effects of partial water saturation on attenuation in massilon sandstone and vycor porous-glass［J］.Journal of the Acoustical Society of America，1982，71（6）：1458-1468.