车辆动载下路基土竖向动应力及扩散规律

刘 伟，汤连生，张庆华

(1.广州市城市规划勘测设计研究院，广东广州 510060;2.中山大学地球科学系，广东广州 510275)

车辆动载下路基土竖向动应力及扩散规律

刘 伟1，汤连生2，张庆华1

(1.广州市城市规划勘测设计研究院，广东广州 510060;2.中山大学地球科学系，广东广州 510275)

推导了车辆动载作用下路基土中竖向动应力的求解方法，提出用速度系数来表征车辆动载下路基顶面产生的竖向动应力与车辆运行速度的关系，并模拟试验确定了速度系数的取值为0.105。原位监测试验表明:车辆动载在路基顶面产生的竖向动应力值约为0～16 kPa，大小与车辆载重及运行速度等因素有关。计算分析了5种类型车辆动载下路基土中竖向动应力的扩散规律。结果显示:随着深度增加，路基土中的竖向动应力逐渐减小，当路基土的深度超过8m时，所有类型车辆荷载在路基土中产生的竖向动应力不到路基顶面的10%;车辆载重越大，竖向动应力扩散速度越慢。

车辆动载;路基土;动应力;速度系数;扩散规律

0 引言

动荷载作用下土体力学行为的研究最早可以追溯到20世纪30年代，在60年代达到较成熟的阶段，主要集中在地震、波浪及机器基础等领域［1］。1965 年，G.Eason［2］研究了多种形式的移动荷载作用下，均质弹性半无限空间的三维稳态响应，他的研究仅限于低音速的情况。D.L.Lansing［3］为了研究爆炸和冲击波，求解了移动点荷载作用下半空间的稳态响应。但很少有学者将移动荷载下半空间稳态响应使用于交通荷载作用下路基土动应力的研究。

1988 年，Hyodo 和 Yasuhara［4］将 10 t重的卡车作为交通荷载以0、10、20、30和35 km/h的速度在试验道路上往复运动，得到了交通荷载作用下不同深度地基的竖向应力，可采用半正弦加载曲线描述。凌建明，等［5］采用基于弹性层状体系，采用荷兰Shell研究工作组的BISAR程序，计算了交通荷载路基顶面及路基土中的竖向应力，分析建立了路基动应力的动力模式，但并没有给出具体的求解方法，而且该程序仍然是基于静土力学理论编制的。王常晶，等［6］研究了列车移动荷载在弹性地基中引起的动力响应问题，认为地基土中动应力分布规律与条形荷载等静力荷载引起的应力分布规律相似。李金风，等［7］探讨了重复荷载作用下沥青混合料的永久变形问题。但到目前为止，交通荷载作用下路基土中动应力时空分布规律等问题并没有解决好，特别是在国内，有关交通荷载下路基土动应力的研究还比较少见。实际工程建设中，路基工后沉降的预测分析仍是将交通荷载简化为静荷载来计算路基土在交通荷载作用下的竖向应力［8］。

笔者通过理论分析和试验研究，探讨了路基顶面竖向动应力与车速之间的量化关系，提出了“速度系数”的概念并确定了速度系数的值。并在Eason［2］等研究的基础上，对车辆动载进行简化处理，建立了车辆动载作用下路基土中竖向动应力的求解方法。通过原位监测试验和数值分析，确定了5种不同类型车辆动载在路基土中产生的竖向动应力沿深度方向的扩散规律。

1 弹性半无限空间竖向动应力的求解

假定大小为P的矩形移动荷载(长、宽分别为2a、2b)作用在弹性无限半空间表面(图1)，荷载以匀速V沿直线运动。引入笛卡儿坐标分量，x轴正方向与荷载移动方向重合，z轴正方向指向半空间内部。半空间任意一点的3个方向的位移分别为u、v、w。半空间位移以图示方向为正，应力以压应力为正，拉应力为负。

图1 移动荷载作用下的弹性半空间模型Fig.1 Model of elastical half space under moving loads

运动平衡方程为［2］:

式中:σx，σy，σz，τxy，τxz，τyz为应力张量的分量;t为时间;ρ为半无限空间的密度;λ、μ为半无限空间的拉梅常数。

根据Eason的研究结果［2］，如果荷载移动速度为低音速(小于瑞利波速)，则弹性半无限空间竖向动应力表达式为:

2 试验模型说明

典型的道路结构一般由路面结构(面层、基层、底基层)和路基土(路基填土层、天然路基土层)组成。试验将道路结构简化为3层结构进行模拟:素混凝土模拟道路结构的面层;中粗砂模拟道路结构的基层、底基层和路基填土层;淤泥质软土模拟天然路基土层。采用电动模型车模拟实际交通荷载进行加载。

试验边界条件根据受力分析确定，道路结构及车辆模型与实际道路相似比为1∶8。

3 速度系数

在求解车辆动载下路基土中产生的竖向动应力时，假定路基土为弹性半空间，其顶部受到面层作用产生竖向动应力与面层的材料、厚度以及车辆的载重、运行速度等因素有关。竖向动应力与车辆运行速度的关系可以用速度系数来描述。

3.1 速度系数的定义

图2为通过室内模型试验得到的路基顶面竖向动应力与车速之间的关系。模型车载重从26～66 kg不等。

图2 路基顶面竖向动应力与车速的关系Fig.2 Relation between dynamic stress and speed of vehicles

式中:qV为车速为V时路基顶面的竖向动应力;q0为静止时路基顶面的竖向动应力。

3.2 速度系数的取值

由图2知，kV(直线斜率)为常量。根据模型试

从图2可以看出，车辆荷载在路基顶面产生的竖向动应力随车速的增加而增大，当车辆载重不变时，动应力与车速基本成正比关系。因此，可用速度系数kV来表征车辆在移动状态下和静止状态下对路基顶面作用力的关系:验得到的不同载重车辆的kV值见表1。

表1 kV与车辆载重的关系Table 1 Relation between kVand load of vehicles

从表1可以看出，车辆动载作用下路基顶面产生的竖向动应力与车辆运行速度大致呈线性相关，速度系数kV为常数，与车辆的大小和重量无关。因此，在计算实际路面车辆动荷下路基土顶面的动应力时，可根据表1确定kV取值约为0.105。

4 路基土中动应力的计算模式

假定路基为均质、各向同性弹性体，力学性能服从虎克定律，路基在水平方向和向下的深度方向均为无限，为弹性半无限空间体。由于车辆荷载并不是直接作用于路基土表面，而是经过面层的作用后才传递到路基土表面，因此，只能把路基顶部受到竖向动应力作为计算路基土中竖向动应力的输入荷载。为简化计算，假定车辆动载对路基顶面的作用位于车辆的前后4个轮胎之间的矩形范围内。同时假定车辆荷载在整个矩形面积上是均匀分布的，荷载速度为V。当V=0时，车辆荷载为静荷载。由于kV为常数，车辆动载在路基顶面产生的竖向动应力与等量静荷载产生竖向静应力与车速成正比，根据公式(8)有:

荷载的长度等于车辆的轴距l1，宽度等于车辆的轮距l2，为矩形荷载，有:

将公式(9)、公式(10)代入公式(4)中，即可得到车辆动载下路基土中竖向动应力的计算公式:

5 数值计算分析

5.1 验证分析

根据公式(11)和公式(12)，计算不同车辆动载条件下路基土中产生的竖向动应力，并与模型试验测试结果进行对比。结论如图3，分别为理论计算得到的竖向动应力(实线)与模型试验测试获得的竖向动应力(虚线)随路基土深度的分布曲线。

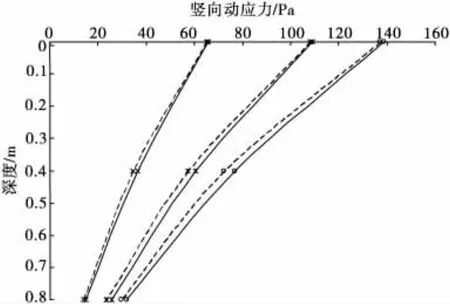
图3 计算结果与试验测试结果比较曲线Fig.3 Curve of academic result and testing result

从图3可以看出，计算结果与试验测试结果基本吻合，误差一般在10%以内。由于文中的试验模型与实际道路相似比为1∶8，在计算实际层状结构路面时，路基土中动应力计算的误差可能会被放大尚需进一步研究。应当指出，若不以应力精确计算为目的而从讨论动、静应力本质特征角度出发，利用文中模型分析动应力特征是合理可行的。

5.2 竖向动应力与荷载强度的关系

图4为通过C++程序计算得到的不同深度上的竖向动应力σz与矩形荷载强度的关系。计算时，l1=6 m，l2=4 m;土层密度ρ=1.8 ×103kg/m3;泊松比 ν=0.3;常数 λ =127.5 MPa，μ =85 MPa;荷载速度V=80 km/h。

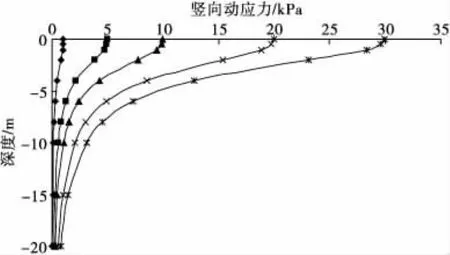
图4 竖向动应力随深度变化曲线Fig.4 Curve of dynamic stress along with depth

从图4可以看出，在车辆动载作用下，路基土中竖向动应力与深度呈非线性关系，随着深度的增加，减小的趋势越来越平缓;在相同的深度上，荷载强度越大，则产生的竖向动应力值越大，竖向动应力与荷载强度基本成正比关系，如图5。

图5 竖向动应力与荷载强度的关系Fig.5 Relation between dynamic stress and load intensity

5.3 竖向动应力与车速的关系

图6为通过C++程序计算得到动应力与矩形荷载速度的关系。计算时，设定矩形荷载边长l1=6 m，l2=4 m;密度 ρ=1.8 ×103kg/m3;泊松比 ν=0.3;常数 λ =127.5 MPa，μ =85 MPa。其中 P 为路基顶面受到的竖向动应力，P=(1+kV)q0。从图6可以看出，当其它条件相同时，路基土中竖向动应力随着车速的增加呈增大的趋势。

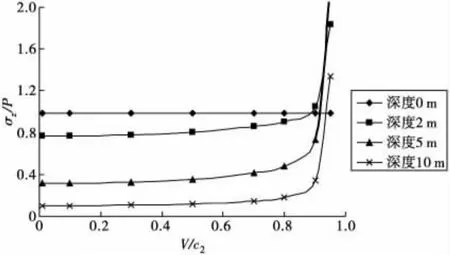
图6 σz/P与V/c2的关系Fig.6 Relation between σz/P and V/c2

需要指出，笔者给出的仅仅是低音速情况下的解。当车速与路基土中剪切波速率比 V/c2＞0.8时，σz/P-V/c2曲线的斜率明显增大;当 V/c2＞0.92时，σz/P＞1，这显然不符合实际情况。一般情况下，土体剪切波速率要远大于公路交通荷载的运行速度，即有 V/c2＜＜0.8。因此，对于车辆动载，公式(11)是适用的。

5.4 竖向动应力与车辆形状的关系

图7为竖向动应力与车辆长宽比(l1/l2)的关系。当l1/l2＜1时，竖向动应力随车辆动载长宽比的增加而增加;当l1/l2＞1时，竖向动应力随车辆长宽比的增加而减小;当l1/l2=1时，动应力达到最大值。说明当车辆载重和面积一定时，车辆的长宽比越接近于1，则相同深度上路基土中产生的动应力值越大。

图7 竖向动应力与车辆形状的关系Fig.7 Relation between dynamic stress and vehicle shape

6 车辆动载在路基土中的扩散规律

表2为通过原位监测试验后统计得到的5种不同类型车辆动载作用下路基顶面竖向动应力值。结果显示，车辆动载作用下路基顶面竖向动应力变化值在0～16 kPa之间，动应力值随车辆载重的增加而增加，同时与车辆速度、轴距及轮距等因素有关。

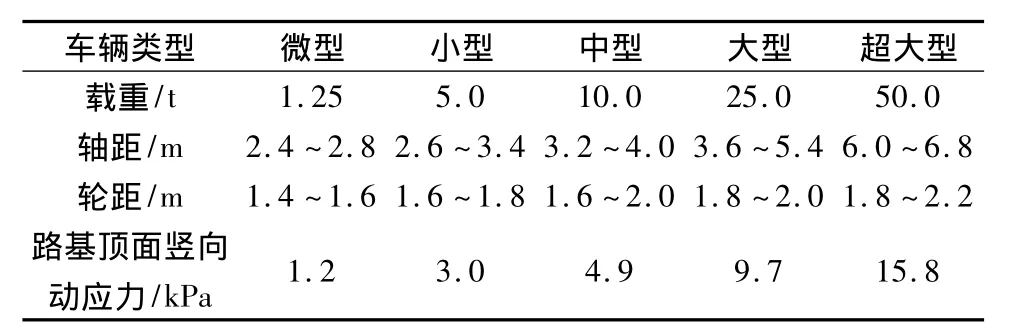
表2 5种车辆动载下路基顶面产生的竖向动应力Table 2 Vertical stress of roadbed under 5 kinds of vehicle load

在5种车辆荷载作用下，路基土中的竖向动应力可以通过公式(11)和公式(12)求解。假定路基为饱和土，一般饱和土拉梅常数 λ=127.5 MPa，μ=85 MPa;密度 ρ=1.8 ×103kg/m3;泊松比 ν=0.3，车速80 km/h。计算结果如图8。

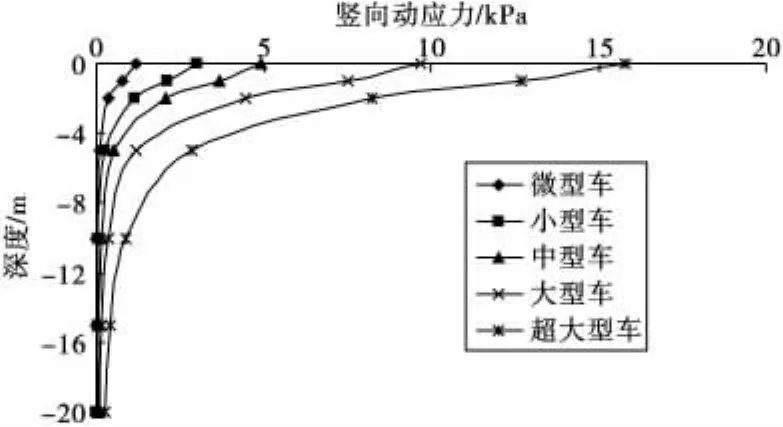
图8 竖向动应力随深度分布曲线Fig.8 Curve of dynamic stress varing with depth

从图8可以看出，随着深度增加，车辆动载在路基土中产生的动应力逐渐减小，在相同的路基土深度上，不同类型车辆荷载产生的竖向动应力水平是不同的，车辆载重越大，则竖向动应力强度越高。对于微型车，在4 m左右的深度上，竖向动应力减小约90%;对于超大型车，在8 m左右的深度上，竖向动应力减小约90%。说明竖向动应力在路基土中的扩散速度还与车辆动载类型有关，越是大型车，在路基土中产生的竖向动应力沿深度方向的扩散速度越慢。

7 结语

1)结合室内模型模拟试验，推导了车辆动载作用下路基土中竖向动应力的求解方法，理论计算结果符合试验测试结果。

2)首次提出了速度系数的概念，表征车辆动载下路基顶面产生的竖向动应力与车辆运行速度的关系。通过模型模拟试验，确定了速度系数的值为0.105。

3)原位监测试验表明，车辆动载作用下路基顶面产生的竖向动应力随车辆动载的强度增加而增大，并与车辆速度、轴距及轮距等因素有关，竖向动应力值在0～16 kPa范围内变化。

4)车辆动载在路基土中产生的动应力随着深度增加而逐渐减小，其扩散速度与车辆荷载类型有关，越是大型车，竖向动应力扩散速度越慢。对于微型车，在4 m左右的深度上，竖向动应力减小约90%;对于超大型车，在8 m左右的深度上，竖向动应力减小约90%。

［1］刘汉龙，余湘娟.土动力学与岩土地震工程研究进展［J］.河海大学学报.1999，27(1):6-15.

Liu Hanlong，Yu Xiangjuan.Advance in soil dynamics and geotechnical earthquake engineering［J］.Journal of Hohai University，1999，27(1):6-15.

［2］Eason G.The stresses produced in a semi-infinite solid by a moving surface force［J］.International Journal of Engineering Science，1965，2:581-609.

［3］Lansing D L.The Displacements in an Elastic Half-Space due to a Moving Concentrated Normal Load［R］.Washington，D.C.:Technical Report R-238，National Aeronautics and Space Administration，1966.

［4］Hyodo M，Yasuhars K.Analytical procedure for evaluating porewater pressure and deformation of saturated clay ground subjected to traffic loads［C］//Proceedings of the sixth International Conference on Numerical Methods in Geomechanics:Volumes 1-3.Rotterdam，Netherlands:AA Balkema，1988:653-658.

［5］凌建明，王伟，邬洪波.行车荷载作用下湿软路基残余变形的研究［J］.同济大学学报:自然科学版，2002，30(11):1315-1320.

Ling Jianming，Wang Wei，Wu Hongbo.On residual deformation of saturated clay subgrade under vehcile load［J］.Journal of Tongji U-niversity:Natural Science，2002，30(11):1315-1320.

［6］王常晶，陈云敏.列车荷载在地基中引起的应力响应分析［J］.岩石力学与工程学报，2005，24(7):1178-1186.

Wang Changjing，Chen Yunming.Analasis of stresses in train-induced ground［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24(7):1178-1186.

［7］李金凤，梁乃兴，汪鑫洋，等.三轴重复荷载作用下AC-13沥青混合料永久变形试验分析［J］.重庆交通大学学报:自然科学版，2012，31(1):54-58.

Li Jinfeng，Liang Naixing，Wang Xinyang，et al.Analysis of AC-13 asphalt mixture permanent deformation in triaxial repeated load test［J］.Journal of Chongqing Jiaotong University:Natural Science，2012，31(1):54-58.

［8］黎冰，高玉峰，魏代现，等.车辆荷载的影响深度及其影响因素研究［J］.岩土力学，2005，26(增刊1):310-313.

Li Bing，Gao Yufeng，Wei Daixian，et al.Research on influential depth of vehicle loads and its influencing factors［J］.Rock and Soil Mechanics，2005，26(supp1):310-313.

Research on Dynamic Stress of Subgrade Soil under Vehicle Loads and Its Diffused Rule

Liu Wei1，Tang Liansheng2，Zhang Qinghua1
(1.Guangzhou Urban Planning ＆ Design Survey Research Institute，Guangzhou 510060，Guangdong，China;
2.Department of Earth Sciences，Sun Yat-sen University，Guangzhou 510275，Guangdong，China)

It put forward a method to calculate vertical dynamic stress of the subgrade under vehicle loads.Vertical stress of the subgrade soil under moving loads is different from the stress under inmobile loads，which can be described by“speed coefficient”and its value is 0.105.The dynamic stress on the top of the subgrade caused by the vehicle loads varies from 0 kPa to 16 kPa，and it will decrease as depth increases.When the depth of subgrade soil is more than 8m，the dynamic stress caused by vehicle loads is less than 10 percents of the stress on the top of the subgade soil.As the vehicle loads is bigger，the vertical dynamic stress diffuses slower.

vehicle loads;subgrade soil;dynamic stress;speed coefficient;diffused rule

TU411.8

A

1674-0696(2012)04-0799-04

10.3969/j.issn.1674-0696.2012.04.16

2011-12-19;

2012-05-28

国家自然科学基金项目(50279056);广东省自然科学基金项目(07003738);广东省科技计划资助项目(2003C33301，2004B32801002)

刘 伟(1970—)，男，广东梅州人，高级工程师，硕士，主要从事岩土工程、地质工程方面的研究工作。E-mail:liuwei@gzpi.com.cn。