基于改进MD模型的区域交通方式划分预测方法
安文娟,陈 峰
(1. 招商局重庆交通科研设计院有限公司,重庆 400067;2. 北京交通大学 交通运输学院,北京 100044)
基于改进MD模型的区域交通方式划分预测方法
安文娟1,陈 峰2
(1. 招商局重庆交通科研设计院有限公司,重庆 400067;2. 北京交通大学 交通运输学院,北京 100044)
分析了MD模型的基本原理;综合考虑出行时间、费用、安全、方便、舒适等5个因素对出行方式选择的影响,完善了出行牺牲量的量化方法,加入了安全性、舒适性、方便性的量化指标及其量化方法;建立了基于改进的MD模型的区域交通方式分担率预测方法,并提出了预测流程及预测模型中关键变量的求解算法;以沪宁通道内客运方式分担率的预测为实例,对比分析了改进前后MD模型及Logit模型的预测结果。验证了改进后MD模型能较好地模拟区域交通方式选择过程,预测有效可行。
区域交通规划;交通方式划分;MD模型
目前,国内外学者已在交通方式划分预测方法上进行了大量研究,主要研究成果可分为两大类:以统计学为基础的集计模型和以概率学为基础的非集计模型[13]。与集计模型相比,非集计模型所需样本容量小、数据统计处理简单、数据可拓展和再利用、对个体行为分析充分,相对来说预测精度较高,因而应用广泛,逐渐取代了集计模型[4]。按随机效用服从的概率分布不同,非集计模型也可以分为两类,即:Probit模型和Logit模型。其中,Probit模型求解复杂,应用范围窄,只适用于两种运输方式之间的分担率,在综合交通体系快速发展的情况下,几乎已经丧失了实用性;而 Logit模型形式简单,求解方便,实用性较强,目前已经有多种演变形式。
MD(Modal Demand)模型本质上是一种非集计模型,对群体的划分则以交通小区为单位,采用的是集计原则,但用于运输通道交通方式划分时可避免集计思路。MD模型主要用于有客运专线引入时,各运输方式占有客运市场份额发生变化的区域交通规划中。与Logit模型相比,MD模型立足于需求和供给两个层面,始终以OD间存在的各交通方式为处理单元,使各方式之间保持相对独立性,能更好地模拟旅客出行方式选择的过程。但MD模型在表征运输方式的牺牲量时,只考虑了运输时间和费用,忽视了其它方面对旅客出行方式选择的影响,具有一定的片面性。鉴于此,笔者对MD模型进行了改进,提出了基于改进MD模型的交通方式划分预测方法,并用实例说明该方法的实用性。
1 MD模型的基本原理
MD模型的基本原理主要用以下概念和假设进行表述[5]:
1)潜在客运需求Qij
潜在客运需求是指 OD对i至j间所有有出行可能性的出行者总数,它并不考虑出行者的支付能力,也不考虑该出行需要最终能否实现。
2)出行牺牲量Smij
出行牺牲量也可以称为广义费用,是指出行者在旅途中所耗费的金钱、时间、精力等。在MD模型中,假设出行者始终以出行牺牲量最小为原则选择交通方式,且认为出行时间和费用对出行行为影响最大,从而综合两者作为出行牺牲量。用对数表示的出行牺牲量如下:
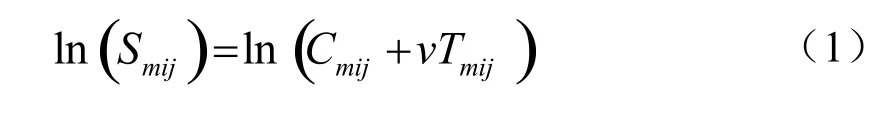
式中:Smij,Cmij,Tmij分别表示OD对i至 j间交通方式m的出行牺牲量、出行费用、出行时间;v为出行时间价值,不同类型的旅客时间价值不同,此类型主要以收入水平、出行目的作为判别标准。在MD模型中,假设时间价值符合对数正态分布,且分布参数随着时间的变化而改变。
3)界限替代率 vm,m-1
若用直线表示出行牺牲量,则交通方式m和m -1的出行牺牲量直线的交点称为界限替代率,可由式(1)推导出,见式(2):
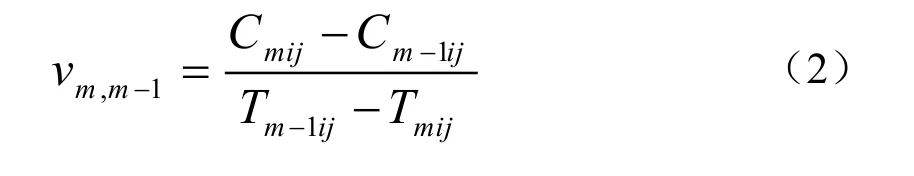
根据界限替代率可推算出不同交通方式的时间价值区间,并可计算各方式的选择比例。
4)出行效用u
在MD模型中,出行效用并非考虑了出行牺牲量后的净效用,是出行者不计出行成本所期望获得的利益,因此只与出行者个体特性(主要指出行目的)相关。不同的出行者,出行效用也不同,与出行时间价值一样,MD模型假设出行效用也符合对数正态分布,其分布参数不随时间而改变;同时假设且出行效用标准差等于出行时间价值标准差。
5)潜在需求显化率Rmij
在MD模型中,只有当出行者的出行效用大于其选择的出行方式的牺牲量时,出行需求才会实施。实现后的潜在客运需求量为实际需求量,两者的比率称为潜在需求显化率:

式中:qmij,Qij分别为OD对i至 j间交通方式m的实际客运需求量,潜在客运需求量。
当交通方式m的出行牺牲量为最小牺牲量时,交通方式m将被旅客选择;且只有当旅客出行效用大于交通方式m的牺牲量时出行才会发生。因此,通过计算时间价值和效用两个概率分布组合点的体积,便可求得潜在需求显化率,式(4)。

式中:f(·)为正态分布概率密度函数。
2 MD模型的改进
出行费用、出行时间、旅途疲劳、安全风险、换乘方便程度均是影响运输方式选择的重要因素。而MD模型仅以出行时间和费用来衡量出行牺牲量,不足以充分刻画出行者选择方式的决策行为。鉴于此,在MD模型的基础上,笔者引入了经济性、快速性、舒适性、安全性等指标来综合衡量出行牺牲量,提出了改进的MD模型。
在改进MD模型中:安全性用安全系数Dmij刻画,该系数是用0~1之间的数值定性地描述交通方式的安全性,数值越大表明安全性越好。安全性是旅客首要考虑的因素,在运输方式的安全性得不到保障时旅客不会考虑该方式,因此,安全性与其它特性之间应是相互独立的。此外,在出行牺牲量中,旅客选择运输方式所付出的“安全费用”由安全系数的倒数表示,表示运输方式的安全性系数越大,其出行牺牲量越小。
舒适性用出行疲劳度Fmij衡量,疲劳度则用疲劳恢复时间gmij与疲劳恢复时间价值 vFm的乘积量化成运输费用的形式,如式(5),且出行疲劳度与费用、时间3者是线性相关的加法关系:

3 基于改进MD模型的交通方式划分预测方法
3.1 预测思路
根据MD模型的基本原理及式(3),预测年t年方式m的实际需求量可以根据其潜在需求量与潜在需求显化率求得,即:

则,旅客选择方式m的概率,即方式m所占的客运需求比例可表示为:
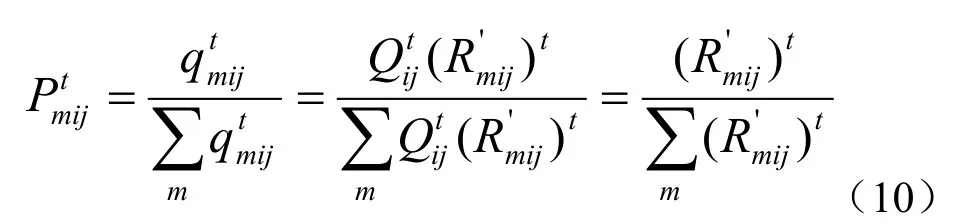
由此,要预测方式m的分担率,关键是求出方式m的潜在需求显化率。
3.2 模型求解
模型求解的关键是出行时间价值、出行牺牲量、出行效用、潜在客运需求显化率等4个变量的求解。
3.2.1出行时间价值估算
时间价值估算常采用Logit模型,参照国内外的研究成果[6],以对出行方式选择影响最大的因素——费用和时间——作为变量,构建运输方式i的效用函数:

式中:ai,bi,ci分别为待估参数;iP,Ti分别为旅客选择方式i所耗的时间和费用。
则,出行时间价值可用两者系数之比表示:

对于效用函数中待估参数的标定,可以根据旅客出行 SP调查数据采用极大似然估计法标定或利用TransCAD软件标定。
出行时间价值与出行者收入水平之间有较大的相关性,而收入水平与GDP直接相关,因此,假设预测年时间价值的方差与基年相同,则,预测年时间价值的均值表示为:

3.2.2出行牺牲量的估算
根据式(6),除了出行时间价值外,出行牺牲量的计算涉及到以下变量的计算:
1)出行费用Cmij
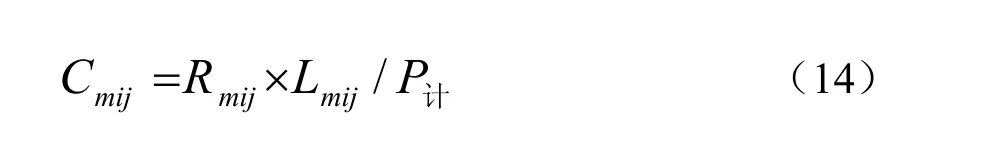
式中:Rmij为客运方式m的运价率,元/(人·公里),客运专线、既有铁路、高速公路、普通公路、民航的运价率分别取 0.35,0.16,0.30,0.17,0.75,小汽车出行费用等于相应的公路运输费用加上油耗费用;Lmij为客运方式m的运行里程,km;P计为计算人数,人,航空、铁路和运营客车取 1,小汽车取平均实载人数。
2)出行时间
出行时间包括乘车时间、候车(机)时间、上车(机)时间、下车(机)时间、到站时间、离站时间。各时间取值见表1[7]。

表1 旅行时间计算取值Tab.1 Parameters’ value of travel time value /h

客运专线 既有铁路 公路 航空到/离站时间 0.70 0.70 0.50 1.20上/下车时间 0.20 0.30 0.10 0.30侯车时间 0.10 0.50 0.35 1.00
3)安全系数的取值
参考已有资料,各方式安全系数取值见表2。

表2 各运输方式的安全系数取值Tab.2 Value of safety factor of various transport modes
4)出行疲劳度的计算
①疲劳恢复时间的计算。疲劳恢复时间与旅客自身身体状况、旅行时间和乘车环境等因素相关。由于旅客个人感受难以量化,因此主要用乘车环境和时间衡量疲劳恢复时间,如式(15):式中: t、δmij、 ρmij分别为OD对i至 j间出行方式m的运行时间、乘车环境量化参数、疲劳恢复时间强度系数,h1;tmax为恢复疲劳所需的最长时间,h。
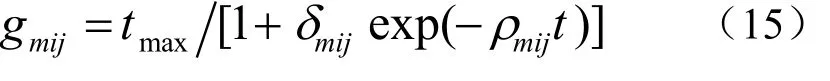
设tmax为15h,则,参数δmij、 ρmij的取值见表3[8]。其中,参数 ρmij≻ 0,其值越大则疲劳恢复时间越长。

表3 参数的取值Tab.3 Value of parameters
②疲劳恢复时间价值的计算。疲劳恢复时间是旅客在旅行完成后身心由疲劳状态恢复到正常状态所耗费的时间。正常情况下,疲劳恢复时间的长短与时间长短存在着一定的对应关系,因此可将疲劳恢复时间归属为旅行时间,疲劳恢复时间价值的估算可借鉴时间价值的计算方法。
3.2.3出行效用的估算
[5],利用MD模型中潜在需求显化
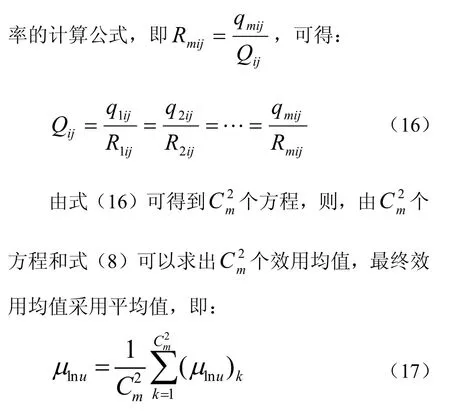
对于预测年出行效用,MD模型假设其均值与现状值相等。
3.2.4潜在需求显化率的计算

4 算例分析
以长三角区域内上海—南京之间的交通方式划分预测为例,利用文中提出的预测方法,以2005年为基年,对算例2015年的交通方式进行划分,进行分析。
已知,上海—南京总里程300 km,沿途经过苏州、无锡、常州、镇江4个重要城市,交通方式以公路和铁路为主,且公路主要指高速公路,铁路包括普通铁路、城际轨道和高速铁路。
根据调查统计的上海—南京的公路、铁路客运量数据及旅客出行特征数据[7],得到各交通方式的出行时间、费用等基础数据见表 4。计算得到2015年旅客出行时间价值均值为3.023;出行时间价值方差为0.234;改进前、后出行效用均值分别为5.243、5.956;出行效用方差均值为0.234。将各参数的值代入模型变量的求解公式中,可计算出预测年各变量的值,见表4。

表4 上海至南京各交通方式客运量分担率预测Tab.4 The calculation values of passenger traffic volume share rates from Shanghai to Nanjing
对比改进前、改进后MD模型的预测结果和Logit模型的预测结果(表5)可知:
1)改进前MD模型与Logit模型的预测结果相比,每种交通方式之间都有一定的差距;改进后MD模型对城际轨道交通和普通铁路的预测结果与Logit模型基本一致。
2)算例区域的宏观社会经济发展水平较高,改进后MD模型预测结果中,普通铁路和公路运营客车所占比例较小。从理论上讲,这与客运需求方式结构的实际演变趋势相一致。
3)上海至南京的高速铁路系京沪高铁沪宁段,属于过路车,其主要功能是服务于北京至上海之间的长途快速客流,对于上海至南京之间短途客流而言,其竞争力明显小于沪宁城际轨道交通,因此改进后MD模型的预测结果最符合实际。

表5 不同模型的预测结果对比Tab.5 Comparison on predictions of different models /%
5 结 语
在秉承MD模型基本原理的基础上,充分考虑旅客自身属性和运输方式服务特性对旅客出行方式选择的影响。利用出行时间、费用、安全系数、疲劳度等指标,综合刻画出行牺牲量;提出了适合区域交通方式划分的MD改进模型;给出了模型的计算流程及其关键变量的求解算法。并以实例表明了该方法的可行性。但MD模型默认出行效用的均值不随时间变化而改变,这与实际情况尚有一定差距,有待进一步改进。
参考文献(References):
[1] Chang Lejoon.A network based model for market share estimation among competing transportation modes in a regional corridor[D]. Washington,D.C.:University of Maryland,2001.
[2] Lijesen M G.A mixed logit based valuation of frequency in civil aviation from SP data[J].Transportation Research:E,2006,42(2):82 94.
[3] 周爱娣.交通方式划分预测模型的研究[J].兰州铁道学院学报:自然科学版,2003,22(3):129 132.
Zhou Aidi.Research on the traffic mode splitting models[J].Journal of Lanzhou Railway University:Natural Science,2003,22(3):129 132.
[4] 王江涛,马驷.预测通道客运分担率的 MNL模型特性变量选取[J].重庆交通大学学报:自然科学版,2010,29(6):947 950.
Wang Jiangtao,Ma Si.MNL model characteristic variables selection on forecasting corridor mode split[J].Journal of Chongqing Jiaotong University:Natural Science,2009,29(6):947 950.
[5] 宋雪梅,蒋阳升,云亮.MD 预测模型的计算方法研究[J].交通运输工程与信息学报,2010,2(8):65 70.
Song Xuemei,Jiang Yangsheng,Yun Liang.Study on the calculation method of MD forecast model[J].Journal of Transportation Engineering and Information,2010,2(8):65 70.
[6] 周伟.旅客时间价值[J].交通运输工程学报,2003,3(3):110 116.
Zhou Wei.The value of passengers[J].Journal of Traffic and Transportation Engineering,2003,3(3):110 116.
[7] 胡军红,李晶.各种运输方式协调发展模式探讨[J].重庆交通大学学报:自然科学版,2009,28(2):294 297.
Hu Junhong,Li Jing.Discussion on patterns of transport modes’coordinated development[J].Journal of Chongqing Jiaotong University:Natural Science,2009,28(2):294 297.
[8] 易富君,邓卫.基于 Nested Logit模型的经济圈交通方式划分方法研究[J].交通运输系统工程与信息,2009,4(9):110 115.
Yi Fujun,Deng Wei.Traffic modal splitting method for economic circle based on Nested Logit model[J].Journal of Transportation System Engineering and Information Technology,2009,4(9):110 115.
Regional Traffic Modal Splitting Method Based on Improved MD Model
An Wenjuan1, Chen Feng2
(1.China Merchants Chongqing Communications of Research and Design Institute Co. Ltd., Chongqing 40006, China;
2.School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China)
With analysis of the basic principles of the MD model and consideration of factors like travel time, cost,safety , convenience, comfort on travel mode choice, this paper improved quantitative method of travel to sacrifice and joined the security, comfort and convenience of quantitative indicators to quantitative methods. Then a MD regional traffic mode split model based on improved forecasting methods was established, and a prediction model in the forecasting process and key variables algorithm was given. Thereafter the validity and practicability of the proposed method was demonstrated by the examples of traffic mode split of Shanghai Nanjing corridor.
traffic modal split; split rate forecast; MD model
U491
A
1674-0696(2012)04-
2011 11 16;
2012 03 27
安文娟(1987),女,湖北黄冈人,助理工程师,硕士,主要从事交通运输规划与管理研究。E mail:anwenjuan0617@163.com。电话:023 62653153。

