单脉冲载荷下伪弹性TiNi合金圆柱壳的响应特性分析

李 丹，唐志平，陶俊林

(1.西南科技大学 土木工程与建筑学院 力学教研室，四川 绵阳 621010;2.中国科学技术大学 近代力学系，合肥 230027)

单脉冲载荷下伪弹性TiNi合金圆柱壳的响应特性分析

李 丹1，唐志平2，陶俊林1

(1.西南科技大学 土木工程与建筑学院 力学教研室，四川 绵阳 621010;2.中国科学技术大学 近代力学系，合肥 230027)

以工程中广泛使用的基本构件——圆柱薄壳结构作为研究对象，利用改进的分离式Hopkinson压杆装置，对不同长径比的PE相变柱壳进行了较为系统的单脉冲轴向加载冲击实验。通过对相变柱壳高速CCD摄影及局部轴向应变的测试发现：不同长径比呈现出不同的屈曲模态。相变柱壳中的相变铰具有以下特点：① 可回复性;② 出现相变铰的时间尺度为微秒量级，与波动效应耦合在一起，变形呈现波动性;③ 多相变铰形成，包括周向相变铰、轴向相变铰和斜相变铰。

单脉冲加载;相变柱壳;相变铰;TiNi合金;伪弹性

形状记忆合金(SMA)作为一种特殊的新型功能材料，是少数兼有感应和驱动功能于一体的智能材料，同时还是一种很好的结构承载材料，具有优良的机械性能。与复合材料和传统的弹塑性材料不同的是，形状记忆合金的变形和吸能机理在于热弹性奥氏体↔马氏体相变。由于SMA的优越特性，各国愈来愈重视其在工程方面的应用。Indirli等［1］将超弹性SMA棒与钢筋连接在一起，对遭受4.5级地震而严重破坏的意大利San Giorgio教堂钟塔进行了修复，分析表明可以吸收更多的冲击能量，降低地震时建筑物的加速度和冲击力。在2000年发生的同震级地震中，修复的钟塔安然无恙，经受住了考验。美国学者研制成超弹性SMA和橡胶复合结构隔振支座［2］改善了多跨简支桥的侧向剪切抗震特性。目前的状况是，国际上有关材料冲击相变的研究十分丰富，工程应用也愈来愈广，但是两者之间的桥梁―基本相变结构件的冲击性能的研究不多，处于起步阶段。在杆和梁方面，Lagoudas等［3］对TiNi合金圆杆进行了动态轴向冲击实验，得到的能量耗散率可达90%。Guo等［4］进行了相变Taylor杆碰撞实验，得到了与弹塑性杆不同的变形和吸能模式。唐志平等［5］、张兴华等［6］分别对圆截面和矩形截面的 TiNi合金悬臂梁进行了横向冲击实验，研究了变形扰度特性和吸能规律，特别观测到相变铰在梁中的形成，发展、移行，消失以及多重相变铰等现象。Nemat－Nasser等［7］用传统的SHPB装置对SMA薄壁圆柱壳的轴向动态屈曲行为进行了初步的研究，得到了动态实验名义应力和应变曲线，但在该SHPB实验中未实现单脉冲加卸载过程，而造成对相变柱壳进行了多次加载。李丹等［8］对TiNi圆柱薄壳轴向冲击加载实验进行数值模拟，结果表明不同的加载强度将会激发出柱壳不同的动屈曲响应模态。目前为止，相变柱壳的单脉冲加卸载响应特性未有系统的研究报道。

借鉴相关学者［9－11］的单脉冲实验研究，我们利用基于Chen单脉冲加载实验原理改进的分离式Hopkinson压杆装置，对不同长径比的相变柱壳进行了较为系统的单脉冲轴向加载冲击实验。利用单脉冲加载方式研究相变柱壳的动屈曲发展演化的主要原因在于：单脉冲加载方式下可以观察相变柱壳完整的卸载恢复过程，加载方式较Nemat－Nasser的相变柱壳轴向动屈曲实验有所改进［7］。

1 实验

1.1 实验装置和试件

实验在宁波大学材料动力学实验室φ7.45 mm口径的经改造的分离式Hopkinson压杆(SHPB)上进行，实验装置如图1所示。实验中所有压杆均采用钢杆，压杆直径8 mm，密度7.81 g/cm3，杨氏模量221 GPa，杆中弹性波波速为5 193 m/s。入射杆长1 012 mm，子弹长度为90 mm。法兰设计为一长8 mm，外直径15 mm，内直径8.00 mm的圆环与入射杆螺纹紧密配合，固定在入射杆的子弹撞击端。试件为TiNi圆柱壳，购自美国NDC公司(Nitinol Devices and Components Co.)，成分为 Ni－ wt%56.1，Ti－ balance，密度 6 450 kg/m3，其奥氏体相完成温度Af=－4.39℃，在室温下处于伪弹性状态。材料基本参数如下：奥氏体相弹性模量为63.7 GPa，相变起始应力、应变分别为478 MPa、0.75%(A点)，相变完成应力、应变分别为580 MPa、5.60%(B点)，逆相变起始应力、应变分别为302 MPa、4.78%(C点)，逆相变完成时应力、应变分别为170 MPa、0.25%(D 点)，相变平台段模量 33.9 GPa，相变应变(即平台宽度)3.90%，马氏体相弹性模量62.2 GPa。相变柱壳外直径为6.3 mm，壁厚0.15 mm，根据实验要求具有不同的轴向长度。

SHPB测试相变柱壳局部应变整体实验装置如图2(a)所示，将相变柱壳上应变片g1－g4组成的布局设为x－y坐标平面，入射杆端处的壳体圆心位置为原点，壳长度方向为 X 轴，垂直(g1，g3)和(g2，g4)的方向为y轴。图2中g1～g4代表4个应变片，X1～X2代表贴片位置与入射杆端的距离，X3为不同长径比的相变柱壳长度。

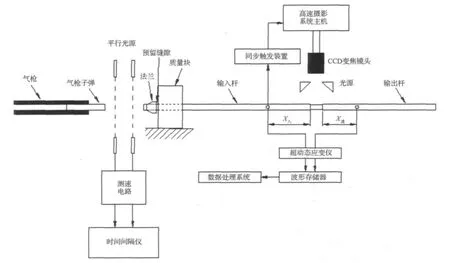
图1 单脉冲加载测试相变柱壳全场屈曲模态装置示意图Fig.1 Schematic diagram of single wave pulse loading set up，testing buckling mode of phase transformation cylindrical shells

1.2 实验结果

表1中所有应变均为圆柱壳的名义应变，临界载荷1及临界应变1为柱壳发生轴对称屈曲时的最大载荷及对应的名义应变。临界载荷2及临界应变2为发生非轴对称屈曲时的载荷及名义应变。最大应变载荷为名义应变最大时所对应的载荷。编号中SS代表两端简支，1.5，2.0，2.5分别代表长径比为1.5，2.0，2.5。

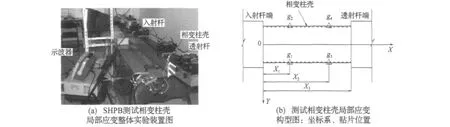
图2 单脉冲动态加载下测试相变柱壳局部应变示意图Fig.2 Diagram of single wave pulse loading set－up，testing local strain of phase transformation cylindrical shells

表1 单脉冲载荷下TiNi圆柱薄壳试件实验动屈曲临界参数Tab.1 Dynamic buckling critical parameters of TiNi thin cylindrical shells specimens for single wave pulse loading

因长径比为2.0的实验结果与长径比为2.5的实验结果类似，这里我们主要给出长径比为1.5和长径比为2.5的典型实验结果，由图3，图4可见，在加载阶段：轴对称屈曲开始于图3(3)点(临界失稳阈值)，此时轴向名义应变为1.37%，超过了TiNi材料的马氏体相变起始应变(0.75%)，说明此前壳体材料已发生部分相变，但柱壳仍处于稳定状态。图3中的名义应力定义为轴向载荷除以试样的初始截面积，名义应变为两端位移差除以试样初始长度。由轴对称屈曲向非轴对称屈曲转换过程中，名义应力下降坡度较缓(图3(3)～图3(5)阶段)，而在非轴对称屈曲深化发展阶段(图3(5)～图3(7)阶段)，名义应力迅速下降，应变向某处集中而其它部位得以部分释放，并在褶皱处出现相变铰，如图3(5)所示。卸载时由于试样两端的位移差要由反射波决定，因此在卸载阶段由反射波形计算名义应变，透射波形计算名义应力。卸载段的卸载时间较长，卸载时间约为240 μs，约为加载时间的5.6倍，卸载速度较慢的原因为：卸载初期卸载速度主要依靠发生较明显相变铰处的壳体较平稳恢复，卸载后期壳体局部应力集中释放，相变柱壳中各处的相成分发生新的变化，壳体进入整体轴压失稳恢复，整个壳体基本处于逆相变混合区，壳体较软，卸载速度进一步降低。壳体的恢复过程主要分为2个阶段：① 靠近两个端部的壳体屈曲部分的卸载恢复过程(图4(9)～图4(12));② 试件中部的壳体屈曲恢复过程(图4(13)～图4(19))。从以上分析可看出，长径比较短的相变柱壳先发生轴对称屈曲，接着轴对称屈曲向非轴对称屈曲转换，非轴对称屈曲模态随着脉冲载荷的增加进一步深化发展。

图3 实验1得到的单脉冲动态名义应力和应变曲线(试样SS－1.5，弹速为19 m/s)Fig.3 Variation of stress with nominal strain of experiment 1(specimen SS－1.5，bullet speed is 19 m/s)

图5是试样SS－2.5(实验3)的名义应力－应变曲线，图6是其对应的高速CCD记录图像，两图中的数字编号一一对应。图6(1)～图6(7)为加载阶段，由于图6(1)～图6(2)阶段靠近入射端的壳体出现了微小屈曲波纹，对应的名义应变曲线有一个峰值。在出现此微小屈曲波纹后，绝大部分壳体仍然具备足够的刚度来抵抗外界变形，随着名义应变的增加，名义应力继续增加，因此图6(2)～图6(3)阶段的名义应力应变曲线处于一个上升趋势。

图4 实验1的高速CCD记录图像Fig.4 High－speed CCD photographs of experiment 1

图5 实验3得到的单脉冲动态名义应力和应变曲线(试样SS－2.5，弹速为20.4 m/s)Fig.5 Variation of stress with nominal strain of experiment 3(specimen SS－2.5，bullet speed is 20.4 m/s)

图6(3)～图6(5)加载过程中端部出现不明显的轴对称屈曲波纹，图6(5)～图6(7)端部出现明显的菱形非轴对称屈曲波纹，其最大名义应变为3.05%，临界屈曲载荷1 112.7 MPa，图6(8)～图6(16)为主要卸载段，记忆合金壳体恢复初始形状，随后壳体发生自由振动过程，直到入射杆和透射杆与相变柱壳脱离，如图6(17)所示意。加卸载全过程历时约为194.4 μs。相变柱壳卸载段的卸载时间较长，时间为151.4 μs，约为加载时间的3.52倍。卸载时相变屈曲皱褶恢复过程与长径比为2.0时基本相同，图6(7)～图6(10)阶段靠近入射杆端的壳体应力释放，相变屈曲皱褶逐渐消失，在此阶段透射杆端的壳体局部应变基本保持不变，图6(10)～图6(16)阶段透射杆端处的菱形非轴对称屈曲皱褶逐渐恢复，过程持续时间较长。

在两端简支情况下，不同长径比的相变柱壳呈现出不同的屈曲模态，且在加载后期都发生了非轴对称屈曲，解释原因为：圆柱壳在轴向冲击载荷下会发生拉压和弯曲两种主要的变形，其中拉压刚度和壳厚成正比，而弯曲刚度与壳厚的立方成正比，因此当径厚比较大时(薄壳)，圆柱壳抵抗拉伸或压缩的能力比抵抗弯曲大得多，为了获得较低应变能的位移，使壳体中面保持最小的拉伸状态，菱形是可以满足这种要求而形成的曲面。与弹塑性柱壳的塑性弯曲屈服所形成菱形的棱不同在于，相变柱壳中的菱形的棱是由于相变屈曲而形成的，为了吸收更多的能量，壳体将尽量增加单个菱形波形的总长度。

从三种不同长径比的相变柱壳单脉冲实验可总结以下规律：在加载早期，短壳形成的轴向屈曲波纹比长壳的屈曲波纹数多(图4(4)，图6(4))，其原因为对于差别不大的外界冲击能量，较长的相变柱壳受边界影响较大，两端容易失稳，因此形成局部屈曲环吸收能量，使壁厚增加，提高壳体的抗弯能力，而较短的柱壳在同样的动态载荷下，应力分布较均匀，可通过形成较多的屈曲波纹来吸收冲击能量。在加载后期，长径比为1.5的壳在试件中部形成三个菱形屈曲波纹，两端位置有微小皱褶产生(图4(5))，整个壳体基本都参与了屈曲失稳。长径比为2.0，2.5时，在试件端部各有三个菱形屈曲波纹产生(图6(5))，呈现非轴对称金刚石屈曲模态。高速CCD图像中呈现的屈曲波纹是由若干个相变铰组合而成，相变铰的形成发展具体分析见下文。

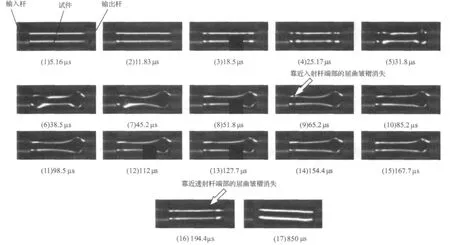
图6 实验3的高速CCD图像Fig.6 High－speed CCD photographs of experiment 3

2 不同长径比的相变柱壳中屈曲模态和相变铰的形成发展

通过三种不同长径比的相变柱壳单脉冲实验结果，获得了不同试件截面的屈曲演化过程，结合以往典型金属柱壳三维变形模式，将动态加载下相变柱壳三维中的相变铰的形成演化过程，按照屈曲皱褶的演化发展方向分为周向相变铰，轴向相变铰，斜向相变铰，给出类似的动态载荷下不同长径比下相变铰的分布示意图，如图7所示。

其中图7(a)表示长径比为1.5的相变柱壳中靠近入射杆端的轴向相变铰长度L1约等于2.59 mm，与靠近透射杆端的轴向铰长度L3相等，中间菱形屈曲波纹的长度L2约等于3.55 mm。由图7观察相变柱壳不同长径比的全场屈曲模态演化，统计其相变较个数，长径比为1.5时生成的相变铰个数达到24个，长径比为2.0和2.5的相变柱壳中生成的相变铰个数达到36个。

3 典型实验中局部轴向应变的测试及分析

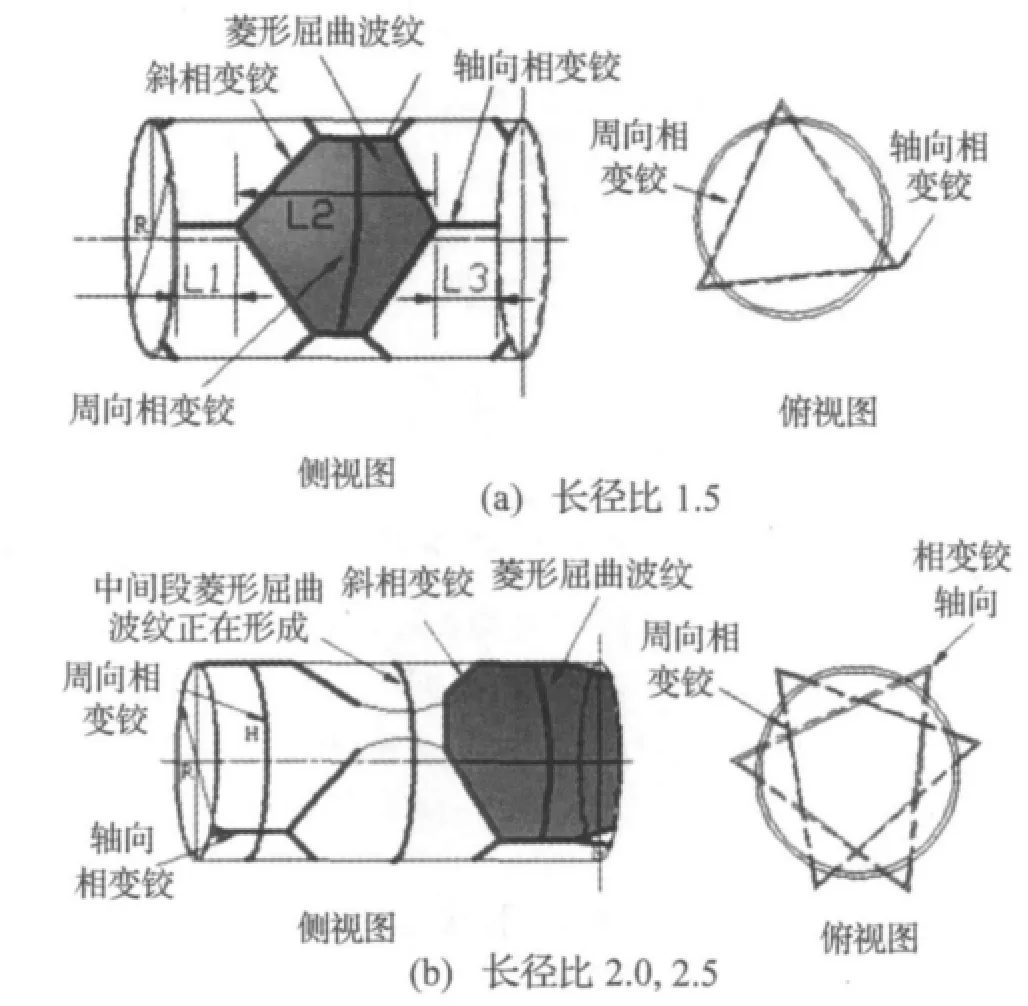
图7 不同长径比下的柱壳相变铰示意图(最大名义应变下)Fig.7 Diagram of phase transformation hinges under different length－diameter ratio(maximum nominal strain)

根据郭扬波［12］的三维相变临界准则和相变材料的一维本构关系，判断局部壳体发生正相变和逆相变的准则如下：当单脉冲轴向载荷刚进入壳体时，此时轴向应变为主要应变，可近似按一维应力状态考虑，即当测点处轴向应变达到0.75%，测点处的壳体开始发生正相变。逆相变完成定义为测点处壳体由混合相完全转化为奥氏体相。壳体出现局部屈曲波纹后应力状态较复杂，周向应变在某些位置超过轴向应变，取逆相变完成时的等效应力为σi。根据等效应力关系(式(1))，编制FORTRAN程序，寻找合适的应力组合(三个主应力取值范围为0到一维逆相变应力)，逆相变应力取值依据出厂材料参数，取为170 MPa。根据Mises准则，假设当Mises应力达到逆相变应力，认为逆相变完成，以此求得轴向应力(主应力方向之一)的取值范围。通过应力反推应变，根据三维应力应变关系(式(2))求得轴向应变的取值范围为：卸载时测点处逆相变完成时轴向压应变介于0.08% ～0.13%，轴向拉应变介于0.36% ～0.43%。

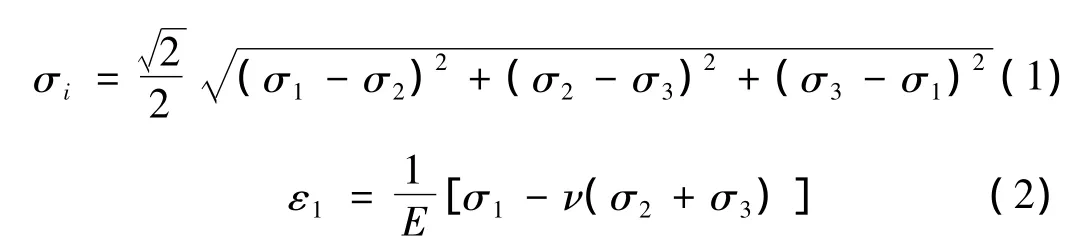
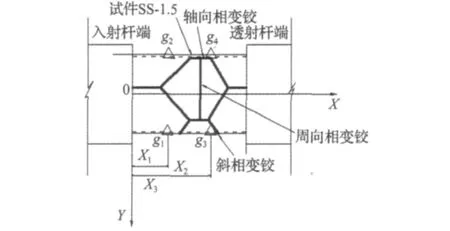
图8 单脉冲动态加载下测试相变柱壳局部应变示意图(试件SS－1.5)Fig.8 Diagram of single wave pulse loading set－up，testing local strain of phase transformation cylindrical shells(specimen SS－1.5)

利用试件SS－1.5进行了子弹撞击速度为11.9 m/s的单脉冲加载实验：4个应变计在壳中位置与相变铰形成的相对位置如图8所示，g1，g3分别距离入射杆端X1=3.5 mm，X2=6.5 mm，g2，g4则分别对称贴在与g1，g3相对应的位置。图8中可看到，g3靠近斜相变铰，g4靠近轴向相变铰。测得的波形如图9所示，4个应变计均记录到了完整的加卸载应变波形。撞击过程中，入射杆向相变柱壳内部传入一梯形载荷，使相变柱壳发生屈曲变形，在压缩应力波的作用下，壳体产生轴向受压变形，弯曲应力波促使壳体径向变形。根据测量波形判断，实验中4个应变片贴片处均发生了相变，其中g4处出现了较明显的轴向相变铰。试件SS－1.5单脉冲载荷下的加卸载时间大约为283 μs，波动响应和整体结构响应耦合在一起，图9给出了300 μs内的应变波形，在13.2 μs～14 μs左右4个应变片的应变达到相变临界应变0.75%(图9(a)中的a点，图9(b)中的c点)，表明4个应变片所在位置的表层材料均开始发生相变，之后应变持续增加，促使壳体整个截面进入相变区，到30.4 μs时g2达到最大值1.81%图9(b点)，其他位置的应变也逐渐增大，最大轴向应变达到1.2%以上。对于靠近透射杆端与g2处于同一轴线的g4，在32.6 μs时轴向应变达到最大值1点(1.36%)，在37.8 μs时刻由压应变转化成拉应变，表明g4处此时出现了较明显的轴向相变铰，此后较长一段时间都处在相变区，直至191.4 μs左右，g4应变降到Ⅳ区域，逆相变完成。靠近斜相变铰的g1和g3都处在受压状态，g1处的波动性表现得较为明显，在加卸载过程中呈现出8次极大值(图9中用数字编号表征波峰、波谷)。而在卸载的大部分时间都处在相变区。在44.8 μs左右g2应变降低到Ⅱ区域，说明g2处的应力很快得到释放，在114.8 μs左右g1应变降低到Ⅰ区域，到171.8 μs左右相变铰处g3的应变降低到Ⅲ区域，逆相变完成，说明相变铰处的应力在卸载过程中维持时间较长，释放较为缓慢。

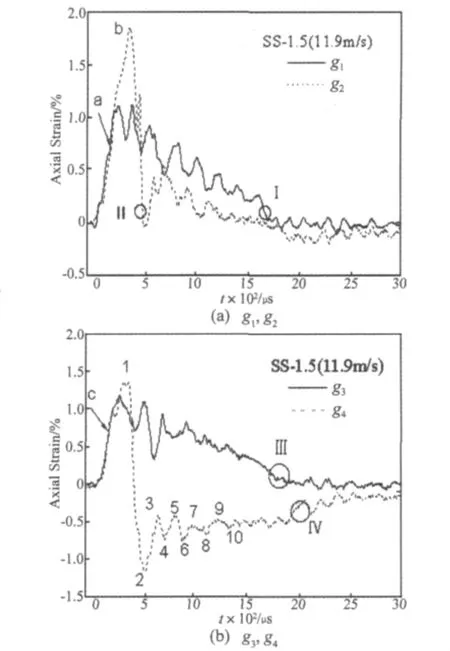
图9 弹速11.9 m/s时试件上应变片的实验波形(试件SS－1.5)Fig.9 Experiment strain profiles for bullet speed is 11.9 m/s(specimen SS－1.5)

4 结论

通过高速CCD摄影及局部轴向应变的测试，研究了单脉冲载荷下相变柱壳的加卸载响应特性，结果表明：

(1)长径比较短的相变柱壳发生较明显的轴对称屈曲，接着轴对称屈曲向非轴对称屈曲转换，相变壳体基本都参与屈曲失稳;长径比较大的壳体受端部影响较大，加载早期轴对称屈曲波纹不明显，加载后期端部出现菱形非轴对称屈曲波纹。

(2)单脉冲加载过程中多相变铰形成。单脉冲加载下柱壳中的相变铰，按照屈曲皱褶的演化发展方向可分为周向相变铰，轴向相变铰，斜向相变铰。

(3)在相变铰回复过程中相变铰的波动性表现明显。相变柱壳各处的应变不是单调变化的，而是呈现出一种波动性。相变铰处的应力在卸载过程中维持时间较长，释放较为缓慢。

(4)单脉冲载荷下相变柱壳结构响应和波动效应相互耦合。实验1～实验3中出现相变铰的时间为单脉冲载荷进入相变柱壳29 μs～35 μs，可以看出相变柱壳结构响应并出现相变铰的时间尺度为微秒量级，其与波动效应耦合在一起。

［1］Indirli M，Castellano M G，Clemente P，et al.Demoapplication ofshape memory alloy devices［J］.The Rehabilitation of the S. Giorgio Church Bell－Tower.Proceedings of SPIE，2001，4330：262－272.

［2］DesRochesR，DelemontM.Seismic retrofitofsimply supported bridges using shape memory alloys［J］.Engineering Structure，2002，24：325－332.

［3］ Lagoudas D C，Ravi－Chandar K，Sarh K.Dynamic loading of polycrystalline shape memory alloy rods［J］.Mechanics of Materials，2003，35(7)：689 －716.

［4］Guo Y B，Tan G Z P，Zhang X H，et al.Phase transition taylor test，WIT transactions on engineering sciences［M］.Alves M，Jones N.Impact Loading of Lightweight Structures.Southampton：Win Press，2005：241－255.

［5］唐志平，卢艰春，张兴华.TiNi相变悬臂梁的横向冲击特性实验研究［J］.爆炸与冲击，2007，27(4)：289－295.

［6］张兴华，唐志平，李 丹，等.冲击载荷下伪弹性TiNi合金矩形悬臂梁结构响应的实验研究［J］.实验力学，2008，23(1)：43－52.

［7 ］ Sia N N，Jeom Y C，Isaacs J B.Quasi－static and dynamic buckling of thin cylindrical shape－memory shells［J］.Journal of Applied Mechanics，2006，73：825 －833.

［8］李 丹，唐志平，张会杰.圆柱薄壳的动相变屈曲行为分析［J］.爆炸与冲击，2009，29(4)：345 －350.

［9］Sia N N，Isaacs J B，Starrett J E.Hopkinson techniques for dynamic recoveryexperiments［A］. Mathematicaland Physical Sciences London.1991：371－391.

［10］ Sia N N，Isaacs J B.Direct measurement of Isothermal flow stress of metals at elevated temperatures and high strain rates with application to Ta and Ta－W alloys［J］.Acta Mater，1997，45：907.

［11］ Song B，Chen W.Loading and unloading split Hopkinson pressure bar pulse－shaping techniques for dynamic hysteretic loops［J］.Experimental Mechanics，2004，44：622 －628.

［12］郭扬波.TiNi合金的冲击相变特性和相变本构研究［D］.合肥：中国科学技术大学，2005.

Response of TiNi cylindrical shells under single wave pulse loading

LI Dan1，TANG Zhi－ping2，TAO Jun－lin1
(1.School of Civil Engineering and Architecture，Southwest University of Science and Technology，Mianyang 621010，China;2.Modern Mechanics Department，University of Science and Technology of China，Hefei 230027，China)

Pseudo－elastic phase transformation cylindrical shells(PTCSs)with different length to diameter ratio(LDR)under single pulse loading were tested by using a modified split Hopkinson pressure bar(SHPB)apparatus.It is found that PTCSs with different LDR have different buckling modes and local strains，which can be measured by high speed camera and strain gauges respectively.The phase transformation hinge(PTH)of PTCS is characterized by the following：1.recoverability;2.PTH appears with a microsecond－grade time duration.It is coupled with the fluctuation effect and its deformation is fluctuant;3.there are a number of PTHs in PTCS under impact loading，including circumferential phase transformation hinge，axial phase transformation hinge and diagonal transformation hinge.

single pulse loading;phase transformation cylindrical shell;phase transformation hinge;TiNi alloy;pseudo－elasticity

O344

A

国家自然科学基金资助项目(10872196)

2011－04－11 修改稿收到日期：2011－09－09

李 丹 男，博士，讲师，1975年4月生