基于K-means聚类算法的群体机器人聚集队形控制
杨 萍,郭春阳,李翠明
(兰州理工大学机电工程学院,兰州 730050)
基于K-means聚类算法的群体机器人聚集队形控制
杨 萍,郭春阳,李翠明
(兰州理工大学机电工程学院,兰州 730050)
针对未知环境下的群体机器人形成聚集动态队形的问题进行研究,分析了群体机器人运动控制策略,将K-means聚类算法与复合机体结构队形控制策略相结合,确定群体机器人聚类中心;个体机器人根据局部感知自主产生队形控制行为矢量,奔向目标,躲避障碍物;产生四种行为控制参数,确定机器人运动速度大小及方向;聚集成为圆形并排列成为三角形队形。仿真实验表明了K-means聚类算法与复合机体结构控制策略相结合的可行性和有效性。
群体机器人;K-means聚类算法;聚集队形;行为控制
0 引言
在自然界的众多群体中,如蜜蜂,鸟群、鱼群等不存在一个协调者来协调大量自主的个体,但他们在运动时普遍存在着编队行为,即他们形成某一集合形状或者在运动过程中保持一种相对不变的位置关系,从而使得这些动物能够联合起来更加有效地发现、围捕猎物和抵御捕食者,这对于它们的生存和繁衍具有重要的生物学意义[1]。人们受到自然界中生物的启发:如果群体机器人在执行任务的过程中保持某种队形,可以发挥较大的作用,其中聚集队形控制问题受到广泛的关注。
目前队形控制方法主要有基于行为法、基于leader的队形控制方法、虚拟结构法等[2]。这些方法侧重于使机器人严格的保持某种特定的几何形状,涉及的机器人数量通常较少,当机器人数量发生变化时需要对队形控制方法做出改进。
本文主要研究聚集队形控制策略,目的在于实现群体机器人系统在保持某一队形的前提下,对未知环境做出快速响应,且不限制机器人个体的位置。本文利用K-means聚类算法结合复合机体队形控制策略,实现了对大规模群体机器人的聚集队形控制,在奔向聚类中心的过程中避免机器人之间的碰撞,并且快速聚集形成队形完成任务。
1 基于行为的控制
在基于行为的控制中,机器人以面向任务进行运动控制的分解,基于行为的结构建立了机器人传感器与执行器的直接联系,把传感器数据与机器人的运动结合起来,实现对未知环境的快速响应[3]。具有代表性的基于行为的控制策略为行为包含结构与复合机体结构[4],行为包含结构通过把控制器分解为分层的任务模块来构建控制器的递增式方法,高层可以通过抑制底层的输出来包含他们的作用。具有实时性强的特性,但上层要干涉下层行为的内部功能,系统的底层行为或者其他部分的微小改动都可能导致整个控制器的重新设计。复合机体结构将每个机器人作为一个复合机体,每一个复合机体都是一个自组织的计算单元,复合机体之间以双向交互脉线的形式连接。每个行为复合机体根据从其相邻复合机体获得的反馈和指导而进行自组织。基于复合机体的并发行为组织会达到一个动态平衡状态,在该状态中整个行为控制的每个复合机体都没有剧烈的转换[5]。K-means聚类算法与复合机体队形控制策略相结合,使群体机器人聚集排列成三角形队形。
2 K-means聚类算法
K-means聚类算法是一种监督学习算法,实现对于未知的数据集进行分组,使得同一组数据内部尽可能相似而不同组内的数据尽可能不同[6]。在某一特定子时刻,特定欧式空间内设x1x2…xi(i=1,2,…,n)。依次表示系统中机器人1,机器人2…机器人n。各个机器人躯干外侧装有一圈等间距的传感器,能够探测到临域内是否存在机器人及机器人的位置,各机器人之间通过脉线相互传递信息。将K-means聚类算法应用于未知环境下群体机器人聚集队形控制中流程如下:

(3)n个机器人找到与k个聚类中心的最小距离d(xi,mi),n个机器人归入到与mi相同的簇中。
(4)遍历完所有对象之后,利用公式2重新计算聚类中心mi的值,作为新聚类中心。

其中mk代表第k个簇的簇中心,n代表第k个簇中数据对象的个数。
平方误差准则使聚类结果尽可能的独立和紧凑,即簇内对象的相似度尽可能的高。定义如下:
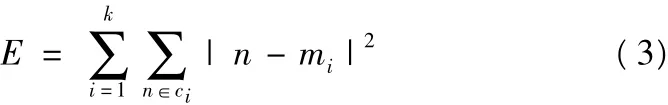
其中E代表所有对象的平方误差的总和,n代表空间中的对象,mi代表簇ci的平均值。
3 聚集队形控制
群体机器人行为的选取是由任务决定的,机器人系统协作聚集运动任务要求各个机器人在不确定的环境下从各自的初始位置运动到目标队形位置,且不能与静态或其他机器人发生碰撞[7-8]。基于K-means聚类算法中,群体机器人在复合机体结构的行为控制策略下将会产生行为库,包括奔向目标行为、躲避静态障碍行为、躲避其他机器人行为、保持队形行为。每个行为的输出都会产生一系列的控制参数,以上四种行为的控制参数产生函数,将会按照实际环境的条件的变化并结合相关信息输出不同的值,以合成方向矢量以适应环境[9-10]。
(1)Move_to_goal:奔向目标行为,产生奔向目标行为输出矢量。方向为由机器人当前位置指向目标位置。Move_to_goal的行为控制参数值随着机器人到目标位置的距离d1的变化而变化。机器人奔向目标行为输出矢量(公式4)及输出控制参数(公式5)定义如下:
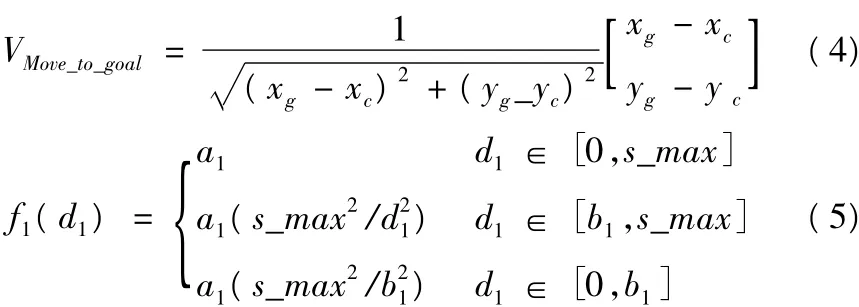
其中[xg,yg]T为目标坐标点,[xc,yc]T为机器人当前位置坐标;a1b1为可调整的参数,且b1与机器人运动的步长有关;s_max为机器人传感器的最大检测范围。
(2)Avoid_static_obstacle:躲避静态障碍行为,输出躲避静态障碍物的行为输出矢量,使得机器人旋转一定的角度以避免与障碍物发生碰撞。机器人躲避静态障碍物行输出矢量(公式6)及输出控制参数(公式7)定义如下:
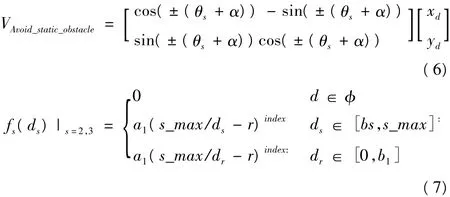
其中θs为机器人当前运动方向与机器人和障碍物连线之间的角度为,±表示机器人的转动方向,其确定与障碍物在机器人的右侧或左侧有关,[xd,yd]T为机器人的运动方向;as,bs为可调整的参数,且bs与机器人的半径有关;d2为机器人与其检测到的障碍物所形成的障碍物区域之间的最短距离;d3为机器人与检测出的其他机器人之间的最短距离;index为当被检测到的物体是静态障碍或其他机器人时取2,动态障碍时取3。(3)Avoid_robot:躲避动态障碍行为,输出躲避动态障碍物的行为输出矢量,当机器人判断出其他机器人有可能影响其运动时,机器人综合障碍的当前位置和预测位置进行决策,产生一个障碍区域,此行为使机器人向左或向右转一定的角度避免发生碰撞。机器人躲避动态障碍与静态障碍的输出控制参数相同见公式(7),机器人躲避动态障碍物的行为公式(8)定义如下:
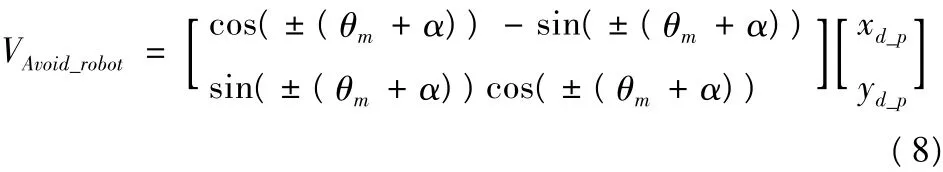
其中θm为障碍物的预测方向与机器人和障碍区域连线之间的最大角度为,±根据预测的障碍运动方向与障碍区域的相对关系确定,[xd_p,yd_p]T为机器人预测的障碍物运动方向。
其中a4b4为可调整的参数,d4为机器人当前位置与理想队形位置之间的距离。
以上所述四个控制参数可以最终确定机器人的运动速度大小及方向。当考虑到Q个障碍物可能阻碍机器人的运动时,机器人最终的运动方向决策如下:
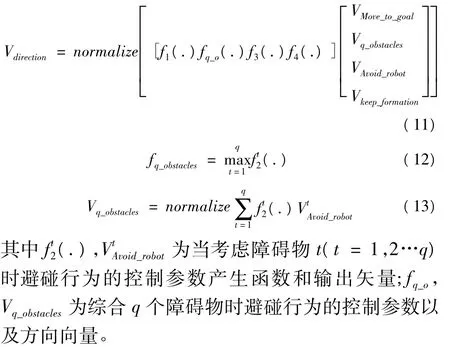
由于机器人聚类中心不需要进行队形保持,因此移动的步长step(.)为0,机器人系统可以根据队形误差灵活的选择机器人聚类中心,在向目标聚类中心移动时,步长为变量。
4 仿真试验与流程
4.1 个体机器人聚集队形控制算法的流程
(1)感知局部环境;
(2)如果达到目标区域则终止,否则继续执行;
(3)计算行为库产生向量及控制参数
①计算VMove_to_goal产生的向量及控制参数;
②计算VAvoid_static_obstacle产生的向量及控制参数;
③计算VAvoid_robot产生的向量及控制参数;
④计算VKeep_formiation产生的向量及控制参数。
(4)根据各控制参数确定机器人的运动速度大小及方向;
(5)转到(1)。
4.2 个体机器人聚集队形控制仿真实验
仿真实验将matlab7.10作为基础实验平台[11-12],仿真实验选取300个机器人,从起始位置,无碰撞的移动到聚类中心,使群体机器人聚集排列成三角形队形。仿真中,机器人都是半径为0.2的圆,传感区域半径为1.8,步长最大为0.5。在Avoid_static_obstacle和Avoid_robot行为中α取π/6,机器人各个行为参数取值见表1。

表1 机器人行为控制参数产生函数中的参数
如图1所示为聚类运动的仿真全过程,图1a为群体机器人以相当混乱的方式分布在空间中,首先随机分布在空间中的机器人随机确定三个聚类中心,这时Move_to_goal起主导作用,机器人朝该聚类中心方向积极运动,在移动的过程中K-means聚类算法会重新计算每个聚类的新质心。在机器人的聚类中心发生变化后,机器人可以立即奔向新的目标。四种控制参数Vdirection确定机器人的运动速度大小及方向。当群体机器人运动到聚类中心附近时,Keep_formation起主导作用。群体机器人保持圆形队形。由于各个机器人分属于各聚类中心,以至于各个机器人不受其他聚类中心的控制及约束。这些分布式的机器人需要经过25次迭代(迭代1次时间为1秒钟)以上才能隐现出一个有效的适应度函数的群体行为。随着集体运动策略的进化,机器人轨迹的运动逐渐变得光滑。迭代121次(121s)以后,机器人之间的协作开始明显,在聚类中心附近可以明显的看到机器人的聚集。225次(225s)之后,可以注意到机器人群体在目标位置附近产生了一个盘旋的运动。这是因为在许多所选择的高适应度个体中,合力排斥的方向可能并不直接指向目标位置。虽然有少量的震荡,但450(450s)次之后群体机器人适应度达到了新的高度,聚集成为圆形并排列成三角形队形。

图1 聚集队形控制仿真实验过程
5 结束语
本文以群体机器人系统为背景,基于行为的控制为基础,结合K-means算法,实现群体机器人在未知、复杂环境中聚集队形的形成和保持。为了能够有效地完成聚集队形控制,防止机器人之间的相互碰撞,快速对外部激励做出反应。本文引入四种行为:奔向目标行为、奔向目标行为、躲避动态障碍行为、保持队形行为。仿真实验说明了队形控制策略的有效性。聚集队形采取分布式控制策略,每个机器人根据自己的局部感知生成自主策略,因此该控制策略具有良好的可扩展性,聚集队形控制策略具广泛的应用前景:在军事上合理的队形结构可以代替士兵执行恶劣,危险环境下的军事任务。在航空航天领域,群体机器人保持队形可以对未知区域进行探索,降低昂贵的费用。
[1]刘衍民,牛奔,赵庆祯.多目标优化问题的粒子群算法仿真研究[J].计算机应用研究,2011(2):64-66.
[2]杨永明,田彦涛,陶军,等.基于社会势场的群体机器人聚集队形控制[J].系统仿真学报,2009,21:187-191.
[3]靳小龙,张世武,吴建兵,等.多智能体模型与实验[M].北京:清华大学,2003.
[4]谭民,王硕,曹智强,等.多机器人系统[M].北京:清华大学,2005.
[5]段晓东,王存睿,刘向东,等.粒子群算法及其应用[M].辽宁:辽宁大学,2007.
[6]屈新怀,高万里,丁必荣,等.基于聚类数和初始值的K-means算法改进研究[J].组合机床与自动化加工技术,2011(4):47-51.
[7]李正义,唐小琦,叶伯生,等.机器人与环境碰撞接触控制研究[J].组合机床与自动化加工技术,2011(5):73-76.
[8]刘海涛,杨乐平,朱彦伟,等.空间机器人工作空间研究[J].组合机床与自动化加工技术,2011(8):32-35.
[9]阳春华,莫志励,李勇刚.基于改进粒子群优化算法的约束多目标优化[J].计算机工程,2010,36:209-211,219.
[10]邹凤山,曲道奎,徐方,等.真空机器人轨迹规划研究[J].组合机床与自动化加工技术,2011(10):18-21.
[11]John H R,Hongyan W.Social Potential Fields:A Distributed Behavioral Control for autonomous robots[J].Robotics and Autonomous Systems(S0921 -8890),1999,27.
[12]Balch T,Arkin R C.Behavior-based Formation Control for Multi-robot Teams[J].IEEE.Transactions on Robotics and Automation(S1552-3098),1998,14.
(编辑 李秀敏)
Swarm Robots Aggregation Formation Control Based on K-means Clustering Algorithm
YANG Ping,GUO Chun-yang,LICui-ming
(School of Mechatronic Engineering,Lanzhou University of Technology,Lanzhou 730050,China)
Unknown environment for groups of robots form gathering dynamics formation problem to study,Analysis groups of robotsmotion control strategy,The K-means clustering algorithm combined w ith composite body structure formation control strategy,Groups of robots to determine the cluster center;Individual perception of self-produce robot formation according to local vector control activities,Toward the goal,A-void obstacles;Produce four kinds of behavior control parameters,Determine the size and direction of the robot velocity,Gathered and arranged into a triangle formation round.Simulation results show that the K-means clustering algorithm combined w ith body structure control strategy feasibility and effectiveness.
groups of robots;K-means clustering algorithm;aggregate formation;behavior control
TH16;TG65
A
1001-2265(2012)08-0089-04
2011-09-14;
2012-01-04
杨萍(1964—),女,哈尔滨方正县人,兰州理工大学机电学院教授,博士,长期致力于CAD/CAM、虚拟设计、机器人等方面的研究工作,(E -mail)yang_ziteng163_com@163.com。

