基于粒子群的粗糙集属性约简与数控机床故障诊断研究*

武 装

(首都经济贸易大学信息学院，北京 100070)

基于粒子群的粗糙集属性约简与数控机床故障诊断研究*

武 装

(首都经济贸易大学信息学院，北京 100070)

数控机床故障诊断的核心任务是根据故障征兆，经过推理计算，自动识别故障发生原因，文章把粒子群算法和粗糙集运用于机械设备的故障诊断中，提出了基于粒子群的粗糙集约简的故障诊断知识获取、规则优化和故障识别。首先介绍了粗糙集属性约简，并把粒子群算法应用于粗糙集属性约简算法中，最后从对相关数据集的约简实验结果角度证明了算法的正确性和优越性。

粒子群;粗糙集;故障诊断

0 引言

数控机床的故障诊断是指根据一定的诊断策略来实施对被诊断系统的检测。通过检测获取诊断对象的故障模式、故障征兆，提取故障特征，并根据预定的推理原则，判断导致系统发生故障的子系统或元素，查明导致故障的原因和性质，并预测状态的发展趋势［1］。目前，在机械设备故障诊断的实践中，由于主客观方面的原因，诊断规则中存在判断条件冗余或不完全、故障征兆描述不确定等现象，不利于实际应用，而粗糙集理论为解决该类问题奠定了理论基础。在数控机床故障诊断领域，应用粗糙集方法可以从诊断数据或诊断案例中提取或优化诊断规则，剔除冗余信息，发现对故障敏感的征兆，找出关键的诊断条件［2］。但在应用粗糙集理论进行属性约简时，往往由于数据量大、样本属性多等因素而不能在有限的时间中找出最小约简。而群智能算法为粗糙集的属性约简提供了有效的途径，粒子群算法是群智能算法的一个重要分支，主要通过模拟了生物种群信息交流的过程来对约简进行迭代搜索，最后得到最小约简或者近似最小约简，因此粒子群、粗糙集等理论方法是数控机床故障诊断技术的一个重要发展方向。

1 基于粗糙集理论的属性约简

粗糙集理论研究的对象是知识表达系统，因此，要在实际中应用粗糙集理论，就首先要把研究的对象表示成粗糙集理论所能研究的形式，也就是知识表达系统。知识表达在整个数据处理的过程中占据着非常重要的位置［3］。通常我们也把知识表达系统统称为信息系统，知识表达系统的数据能够通过关系表的形式进行表示，我们要研究的对象对应为关系表的行，关系表的列则对应着对象的属性，对象的信息是通过指定对象的各个属性值来表达确定的。我们可以看出，每一个属性对应着一个等价关系，一个表我们可以看做是定义的一族等价关系，也就是知识库，因此，知识约简也就可以转化为属性约简［4］。

决策表是知识表达系统中一类特殊而重要的形式，多数决策问题都可以通过决策表的形式来表达，这个工具在决策应用中起到了非常重要的作用。设S=(U，A，V，F) 为一个信息系统，A=C ∪ D，C ∩ D=φ，C称为条件属性，D称为决策属性。具有条件属性和决策属性的信息系统称为决策表。一个决策表中决策属性有时是唯一的，称为单一决策;有时是不唯一的，称为多决策。对于具有多个决策属性的决策表可以变换成为单一决策表，这样有利于问题的简化和求解［6-7］。

决策表的属性约简就是要从条件属性集合中发现部分必要的条件属性，使得根据这部分条件属性形成的相对于决策属性的分类和所有条件属性所形成的相对于决策属性的分类一致，即和所有条件属性相对于决策属性D有相同的分类能力。

决策表的约简步骤如下:

(1)消去重复的行;

(2)进行条件属性的约简，即从决策表中消去某些列;

(3)消去重复的行;

(4)消去重复的冗余值。

对决策表约简的最终结果是将决策表中的知识化成少量的决策规则。信息系统的属性约简研究的是考察信息、系统中的每一个等价关系是否必要以及如何删去不必要的等价关系，达到简化信息系统的目的［8］。

2 粒子群算法及其在属性约简中的应用

2.1 标准粒子群算法

假设在M维搜索域中存在n个微粒，随机组成一个群体。Xi=(xi1，xi2，…，xim) 为微粒 i的当前位置，Vi=(vi1，vi2，…，vim) 为微粒 i的当前飞行速度，Pi=(pi1，pi2，…，pim)为微粒i在优化过程中所经历过的具有最好适应值的位置，Pg=(pg1，pg2，…，pgm)为整个微粒群所经历过的最优位置。其中i=1，2，…，n，且微粒都是M维的。

那么，第t代的第i个微粒迭代到第t+1代，它的第j维速度及位置用以下的迭代方程描述为:

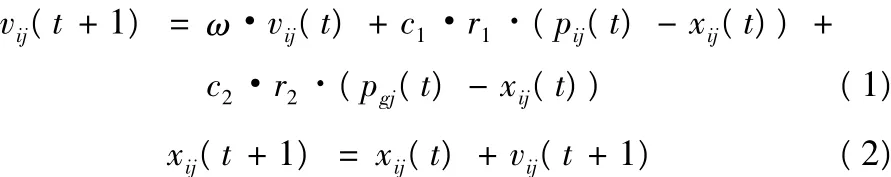
其中，i=1，2，…，n，j=1，2，…，m，ω 为惯性权重，c1，c2为加速常数，r1，r2为［0，1］内两个相互独立的均匀分布的随机函数。惯性权重ω:通常惯性权重取［0.8，1.2］之间的常量，但有时也需要设置一个变量ω让算法迭代达到更好的收敛效果。权重函数ω由下式来确定:

其中，ω的最大值和最小值由 ωmax、ωmin表示，ωmax∈［2，3］，ωmin∈［0.8，1.2］，当前迭代次数和最大迭代次数由 iter，itermax表示［9-11］。

2.2 粒子群优化算法性能测试

我们采用经典的Griewank测试函数对PSO算法进行性能测试。Griewank函数是多峰函数，其最优值为原点。以x代表一个实数类型的向量，其维数为n，而xi为其中的第i个元素。搜索空间范围取|x|＜10，种群粒子数为30，进化代数为10000次。测试的结果如下:

Griewank函数

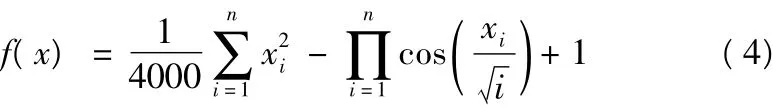
此函数的空间图形如下(空间图形以n=2为例):

从图1中可以很明显地看到，Griewank函数是一个多峰函数，它的最小值为零。

用标准粒子群优化算法计算结果如下:

进化到第400代时得到了全局最小值0。

从上述测试结果可以看出，PSO算法依靠粒子不断地调整位置和速度，通过追随当前搜索到的最优值来寻找全局最优。与其他智能算法相比，PSO算法有效、精度高、收敛快。

图1 二个变量的G riewank函数三维图形

图2 函数在空间|x|＜10的进化情况

2.3 解码设计

属性编码将每个对象属性都转变为相应的正整数，经过PSO优化运算获得适应值最优的微粒，即为信息系统S的一个相对约简。属性解码的设计则是将正整数微粒转变为相应的二进制串码，而这个二进制串就表示S的一个相对约简。他们之间的关系如图3所示。

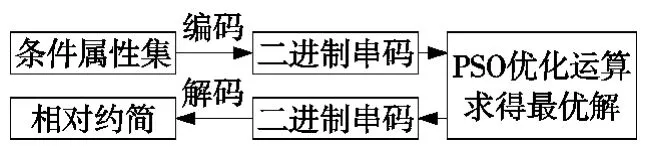
图3 约简转换问题示意图

2.4 算法的框架描述

参照图3的过程描述，将基于PSO算法的粗糙集属性约简过程转换为PSO算法的求解上。在设置合理的PSO算法参数后，求出适应函数最大解对应的微粒，即信息系统的最小属性约简。

算法的具体步骤如下:

输入:信息系统 S=(U，A，V，f)，U 为论域，A=C∪D为属性集合，C和D分别为条件属性和决策属性。

输出:信息系统 S=(U，A，V，f)的一个相对约简。

Step1:随机产生包含w个微粒的种群，每个微粒随机给定初始速度v0和初始位置x0，对x0实数取整;

Step2:对经过迭代产生的微粒位置x实数取整，转化为与属性约简相对应的二进制串，0表示不包含此属性，反之则取1。二进制串的位数由信息系统S的条件属性的属性个数决定;

Step3:查找每个微粒对应的适应度值，若存在，则直接取得;反之则转向Step4计算出微粒的适值;

Step4:计算属性依赖度ki，并对每个微粒中0的个数比 (/m)进行计算。其中m0为微粒0的个数，m为微粒的长度，微粒的适应值fi=ki+/m;

Step5:比较新的适应值、当前适应值和历史最好适应值，确定两个极值pBesti和gBest;

Step6:利用公式(1)，(2)更新微粒的位置xi和速度vi，并对新的位置xi+1和速度vi+1进行范围检查，防止微粒跳出最大搜索范围;

Step7:判断终止条件(即迭代次数)。若条件满足，终止迭代，否则返回Step2，继续循环迭代;

Step8:将最优正整数解转换为二进制串，进而得到属性的相对约简。

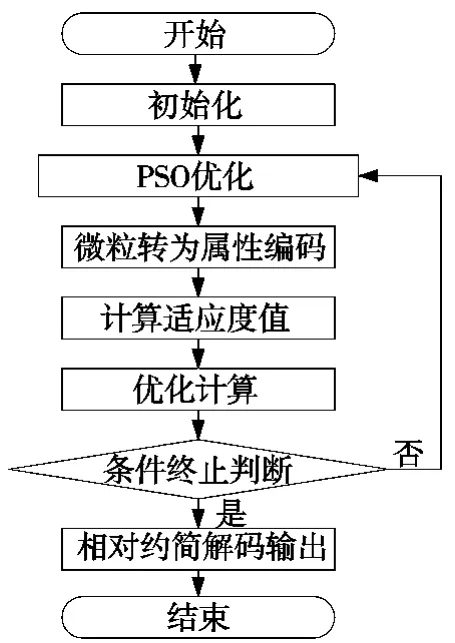
图4 基于PSO粗糙集属性约简算法流程图

3 基于粒子群的粗糙集属性约简算法的故障特征选择与诊断

对于从故障系统中所测得的变量我们并不知道是否为故障相关的特征变量，而我们的目标是要找出一个包含所有相关的故障特征变量的最优子集。由于故障特征选择的对象是一个组合优化问题，所以优化算法中的粒子最好是一组能够表达故障特征变量信息的二进制编码。每个系统变量用1或0表示，当取值为1时，表示其对应的变量被选作为特征变量，若取0则表示对应的特征变量没有被选择。

我们采用基于粒子群的粗糙集属性约简算法来进行故障特征选择。粒子编码示意图如图5所示。

图5 编码示意图

在评价粒子的适应性时，在训练集和测试集的选择方面，一次仿真的原始数据中随机选择正常数据和三种故障数据各200组作为训练集，并从第二次仿真的原始数据中随机选择正常数据和三种故障数据各300组作为测试集，并将上述所得的数据首先进行预处理、去量纲化和归一化后进行相应的故障特征提取和故障特征选择操作。

我们采用约简属性数、达优率和运行时间等几个指标比较和衡量本算法对约简性能的影响。数据包括Vote等6个数据集，包含了属性数多、记录数少，属性数中等、记录数中等，属性数少，记录数多，属性数多、记录数多等几种情况，能够比较客观地评价算法约简性能的好坏，如表1所示。

表1 各个数据集的属性约简结果

从表1约简的效果来看，在所有数据集的约简中，本算法都能取得属性数目相对较少的约简，这是由于本算法在PSO算法良好的寻优能力的基础上，扩大了粒子的搜索空间，取得了较好的效果。

4 结束语

本文把粒子群算法与粗糙集理论应用到数控机床的故障诊断知识获取、规则优化和故障识别中，提出了基于粒子群的粗糙集属性约简算法，丰富完善了机械设备的智能诊断技术。实验结果表明，该算法在收敛速度和寻优能力都得到了改进，这种结合是可行的，并能得到较好的效果，能够很大程度上提高数控机床故障诊断的正确率。

［1］周辉.数控机床常见故障诊断系统软件的开发［D］.北京:北方工业大学，2009.

［2］冯志鹏.计箕智能在机械设备故障诊断中的应用研究［D］.大连:大连理工大学，2003.

［3］赵敏.基于粗糙集理论的属性约简算法研究［D］.湖南:长沙理工大学，2008.

［4］陈展雄.基于多种群免疫量子粒子群的粗糙集属性约简与故障诊断［D］.上海:华东理工大学，2010.

［5］孙英娟.基于粗糙集的分类方法研究［D］.吉林:吉林大学，2011.

［6］张素妍.粗糙集理论在数据融合中的应用研究［D］.北京:北京化工大学，2004.

［7］陈思如.基于PSO的粗糙集属性约简算法研究［D］.湖南:湖南科技大学，2010.

［8］曾正良.基于粗糙集和粒子群的数据挖掘方法研究［D］.湖南:长沙理工大学，2009.

［9］刘爱民，张红奎，张小玲，等.基于多目标粒子群算法的直线感应电机机构优化设计［J］.组合机床与自动化加工技术，2010(9):15－19.

［10］李虹，熊诗波.基于混合粒子群优化算法的故障特征选择［J］.系统仿真学报，2008，20(15):4041－4044.

［11］魏英姿，冯艺君，王洪伟.柔性调度多目标优化的混合粒子群算法研究［J］.组合机床与自动化加工技术，2011(11):109－112.

(编辑 赵蓉)

Study on Attribute Reduction of Rough Set Based on Particle Swarm and CNC Machine Fault Diagnosis

WU Zhuang
(Information College，Capital University of Economics and Business，Beijing 100070，China)

After reasoning computing，fault diagnosis can automatically identify malfunction based on the fault symptoms，this paper uses the particle swarm algorithm and rough set in fault diagnosis，and propose fault diagnosis know ledge acquisition，rules optimization and fault identification based on rough set attribute reduction of particle swarm.Firstly，this paper introduces the rough set attribute reduction，secondly，the particle swarm algorithm is applied to rough set attribute reduction algorithm，finally，the correctness and superiority of this algorithm is proved from the reduction experimental results of related data sets.

particle swarm;rough set;fault diagnosis

1001－2265(2012)08－0051－04

TP277

A

2012－04－29;

2012－05－30

北京自然科学基金项目(9122003);北京市教委专项(00791154430107);北京市哲学社会科学规划项目(11JGB077)

武装(1970—)，男，辽宁人，首都经济贸易大学信息学院讲师，博士，研究方向为人工智能、图形图像等，(E－mail)wuz9080@163.com。