三次非均匀B样条曲线插补算法研究*
林 锋,汪 地
(上海大学CIMS及机器人重点实验室,上海 200072)
三次非均匀B样条曲线插补算法研究*
林 锋,汪 地
(上海大学CIMS及机器人重点实验室,上海 200072)
插补算法的优劣关系到数控加工的精度和速度。文章提出了一种三次非均匀B样条曲线插补算法。该算法基于已知的型值点反算出曲线的控制点,从而得到曲线方程,然后利用泰勒展开公式预估得到曲线插补下一周期的插补点,并通过弓高误差控制方法对曲线插补精度和进给速度进行控制,最后讨论了利用B样条曲线对称性求减速点的方法。经过Matlab仿真分析,证明该方法的正确性与有效性。
非均匀B样条曲线;插补算法;加减速控制
0 引言
对于复杂曲线和曲面的加工,采用B样条插补能:①显著减少NC代码文件的大小,从而提高复杂零件的加工效率;②提高加工的质量和精度,避免了因使用微小直线段插补而带来的以直代曲的误差。文献[1]中提出的参数均匀分割插补算法利用常量增量直接实现曲线插补,插补算法不能控制进给速度,误差较大;文献[2-4]对NURBS曲线直接插补提出了一些插补算法,但由于其控制顶点的权值难以确定,计算量大,不利于插补的响应和实现。因此本文以非均匀B样条曲线为研究对象。通过型值点反算曲线的控制顶点,并求解出曲线方程的矩阵形式,然后基于弓高误差控制约束步长,求得下一个插补周期的插补点。最后为了减少加工时的冲击,采用S型加减速控制,利用B样条曲线的对称性求得减速点。利用Matlab仿真证明该插补算法正确并且精度高,能够满足数控系统插补实时性要求。
1 非均匀B样条曲线的反算
非均匀B样条曲线生成有两种方式,一种是给定控制顶点定义B样条曲线及其导矢,称为正算过程;一种是先给出定位于曲线上的一些点来设计曲线,成为曲线反算,亦称为B样条曲线的逆过程或逆问题。由于通过给定一些曲线上的点来反算曲线控制顶点要比直接给出不位于曲线上的控制顶点更适合设计员的意愿,所以工程实际中,设计曲线一般采用反算曲线的方式。曲线反算过程一般包括两个步骤:①确定曲线节点矢量;②利用边界条件,反算出曲线的控制点[5]。
1.1 非均匀B样条曲线的表示
B样条曲线德布尔-考克思递推方程为:

其中,下标k表示次数,di为控制顶点,Ni,k(u)称为k次规范B样条基函数,其中每一条称为规范B样条。
1.2 三次非均匀B样条曲线节点矢量的确定
给定 m+1 个数据点 qi(i=0,1,…,m),为了使曲线通过这m+1个点,一般总是把首末数据点分别作为非均匀B样条曲线的首末端点,而剩下的m-1的点作为曲线的分段连接点,这时,生成的非均匀B样条曲线将有n+1个控制顶点dj(j=0,1,…,n),其中 n=m+2。节点矢量为 U= [u0,u1,…,un+k+1],采用规范累积弦长法,至此节点矢量完全确定。
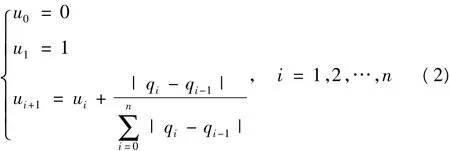
1.3 反算三次非均匀B样条插值曲线的控制顶点
我们将曲线定义域 u ∈[ui,ui+1]⊂[u3,un+1]内的节点值(2)依次代入方程(1),并取自由端矢条件,便可求得曲线的控制点。对于给定控制点序列{d0,d1,d2,…,dn} 和节点矢量{u0,u1,…,un+k+1} 的非均匀B样条曲线,为了减少样条曲线插补中实时计算的工作量,可以将求得的3次非均匀B样条曲线方程化为矩阵形式,转换方法为:对于定义域内节点列U={uk,uk+1,…,un+1},记:


2 非均匀B样条曲线的插补算法研究
2.1 插补预处理
为了减少非均匀样条曲线插补实时计算的工作量,我们可以将插补算法中可一次性计算出的任务放到插补预处理阶段,这样的任务主要包括轨迹表达式系数的求取和导数表达式系数的求取。
将上式和XX式比较,即可求出计算出轨迹表达式的系数。
另外在非均匀B样条曲线插补过程中需计算弧长对参变量的变化率ds/du之值。为减少算法的实时计算的工作量,ds/du式中的有关系数可在预处理阶段求出。
2.2 实时计算
2.2.1 参数的密化
设参数u关于时间t的函数为u=u(t),对时间t进行泰勒展开,有:

对于一般插补,一阶泰勒展开即可满足要求,这时把XX式代入XXX式即可得到插补下一周期的参数值ui+!为:

2.2.2 弓高误差控制
由于上述算法计算的插补点全部落在曲线上,所以非均匀B样条曲线插补不存在偏差,但从插补原理上可知插补过程是以直代曲的过程,它用微小直线去逼近曲线,所以不可避免地引起了弓高误差,其误差随着进给步长和被插补曲线的曲率变化而变化,为了保证弓高误差在允许的范围之内,必须使插补步长随曲率变化而自动调整。如图1所示。由图可求出弓高误差hi、插补步长ΔLi和曲线曲率半径ρi三者之间的关系为:

图1 弓高误差

曲线曲率半径的计算过程如图2所示。
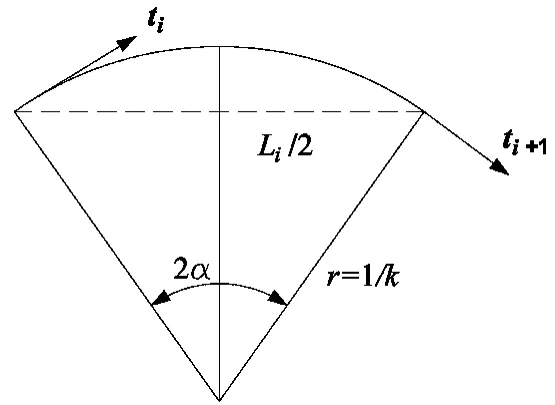
图2 曲率近似计算图
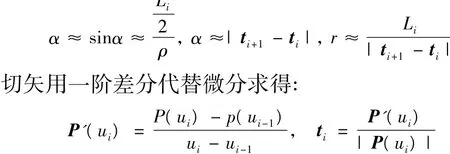
综合上述公式即可求出曲线曲率半径ρi。
基于进给加速度控制的进给步长ΔLi1和上述弓高误差控制的进给步长ΔLi2,得到最终用于插补计算的进给步长为:
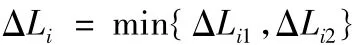
2.3 加减速控制
非均匀B样条曲线插补由于用于复杂曲面零件的加工,所以加减速比较频繁。本文采用S型加减速模式,这种方式不存在速度突变,过渡平滑,并且其加速过程处理也比较简单,而减速点的预测问题是其关键问题。
由于B样条曲线具有对称性,我们可以利用这一特性计算加减速控制的减速点,具体原理为在加速阶段插补的同时,利用对称性同时记录反向插补参数,当正向加速阶段结束时,停止反向插补并记录此时的反向插补参数值uo,当正向插补参数值un≥1-uo时,按S型的减速规律开始减速。
3 非均匀B样条曲线的插补算法仿真
本文以三次非均匀B样条曲线为例,取样条曲线的型值点为:(0,15),(10,2),(24,15),(30,13),(38,8),(50,24),(62,6),(70,20),(80,8),根据第二节所述的反算算法,采用matlab2010编程,可求出节点矢量为:{0 0 0 0 0.1664 0.3380 0.4101 0.4753 0.6058 0.7300 0.8541 1 1 1 1}。根据反算算法求出三次非均匀B样条曲线的控制顶点为:

其中三次非均匀B样条的仿真图形如图3所示。
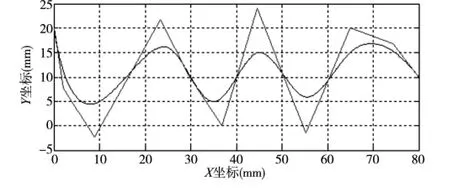
图3 三次非均匀B样条曲线仿真图
假设机床允许的进给速度为300mm/s,插补周期T=1ms,弓高误差最大允许值为hmax=0.001mm,加加速度J=48000mm/s3,加速度最大值amax=2400mm/s2初始进给速度fs=0调用上述第三节所述的插补算法,在Matlab2010软件中进行仿真,得到非均匀三次B样条曲线的插补轨迹如图4所示,其插补弓高误差和插补进给速度分别如图5和图6所示。

图4 插补轨迹仿真图
此插补算法共需插补661步,部门插补结果如表1所示。
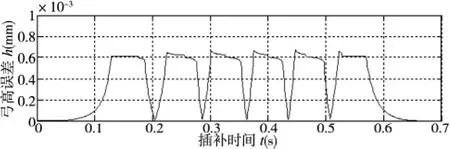
图5 插补弓高误差
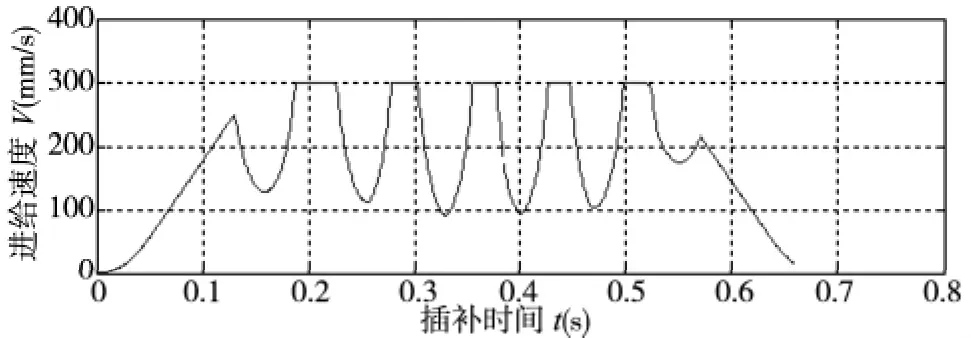
图6 插补进给速度
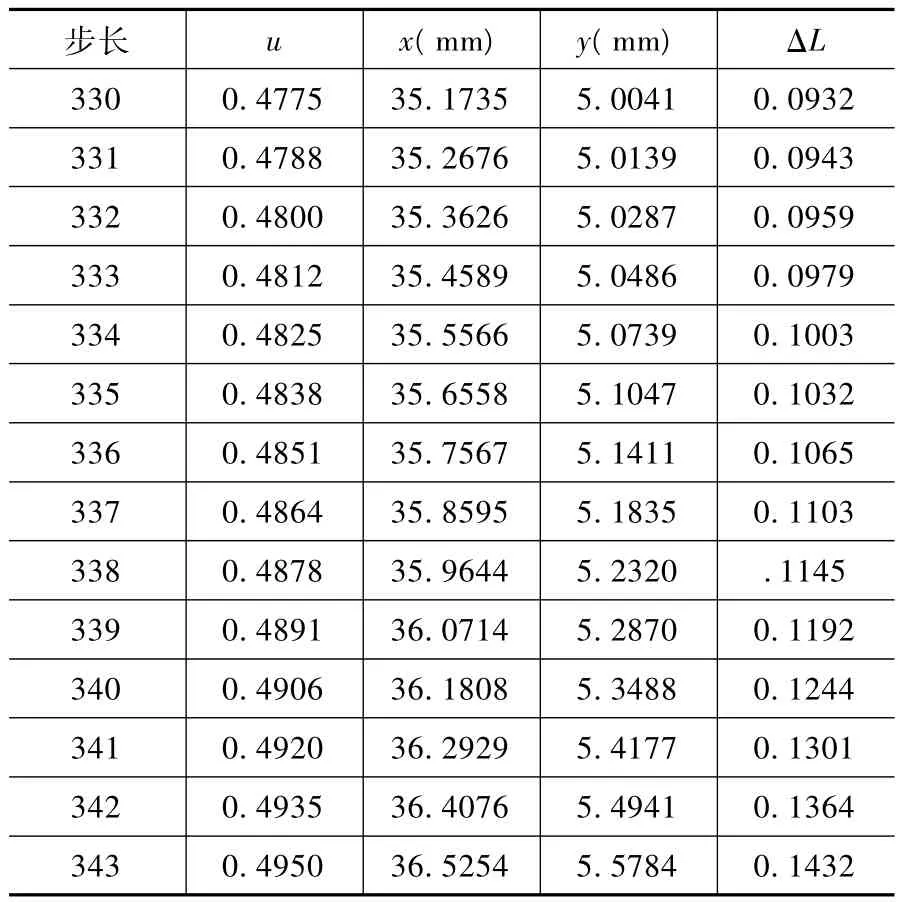
表1 三次非均匀B样条曲线插补结果部分参数值
由上述插补实例可以得出,本文提出的插补算法的正确的、有效的,满足高速高精度非均匀B样条曲线插补的实时性要求。
4 结束语
(1)通过比较插补仿真轨迹和理论曲线证明利用本文提出的插补算法完全正确,其中插补周期为1ms,插补步数为661步,所以该插补算法能够满足数控系统实时性的要求。
(2)基于弓高误差控制约束步长,在满足误差要求的基础上,实现了插补精度和插补速度的自动控制。
(3)利用B样条曲线的对称性预测减速点,算法计算简单,可靠、位置精度高
[1]BEDIS,ALII,QUAN N.Advanced interpolation techniques forNCmachines[J].Journal ofEngineering for Industry,1993,115(8).
[2]刘宇,戴丽,刘杰,等.泰勒展开NURBS曲线插补算法[J].东北大学学报,2009,30(1):119-122.
[3] Zhang Deli,Zhou Laishui,Intelligent NURBS Interpolator Based on the Adaptive Feedrate Control,Chinese Journal of Aeronautics,2007(5).
[4]贾庆祥,徐知行,刘新山.基于阿当姆斯算法的NURBS曲线插补[J].吉林大学学报,2009,39(1):218-221.
[5]施法中.计算机辅助几何设计与非均匀有理 B样条[M].北京:高等教育出版社,2001.
(编辑 李秀敏)
A Study on Interpolation Technique of Non-uniform B Spline Curve
LIN Feng,WAND Di
(CIMS& Robot Center,Shanghai University,Shanghai200072,China)
Interpolation algorithm have a direct impacton the process quality of CNC.An Non-uniform B Spline Curve interpolation algorithm was introduced.Based on the curve’s data points,the control points of the curve was calculated,and the B-Spline cur-ve equation was calculated.The interpolation parameter was approximated through the first and second order Taylor expansion.The controlling chord error was applied to co-ntrol the accuracy and the feed rate.The papermakes use of B-Spline curve symmetry to predict decelaration-point in the real-time interpolation.the interpolation algorithm was proved to be effective by Matlab.
non-uniform B spline curve;interpolation;acceleration/deceleration control
TP271+.4
A
1001-2265(2012)08-0032-04
2011-12-07
上海市机械自动化及机器人重点实验室开放基金
林锋(1987—),男,湖南邵阳人,上海大学在读研究生,从事数控技术、嵌入式运动控制系统方面的学习研究,(E-mail)hyit28@126.com toy1141@shu.edu.cn。

