金属管(杆)横驻波演示实验
路峻岭,王长江,秦联华
(清华大学物理系,北京100084)
1 引 言
金属管(杆)弯曲振动实验是一个有趣的演示实验,所用器材仅为1根薄壁钢管或铝杆和1个橡胶锤.实验者捏持住金属管(杆)中距管端0.224倍管长处,用橡胶锤敲击金属管(杆)的端点或中点,就能听到金属管(杆)发出清晰的声音.若捏持不变,手持橡胶锤敲击金属管(杆)上其他点,会听到金属管(杆)发出声音的音调和音色都有变化.若改变捏持点,敲击金属管端点或中点,也听到声音的音调和音色都有明显变化.若捏持0.224倍管长处敲击中点或端点,仔细聆听常常能听到拍音.若调整捏持0.224倍管长处的点的位置,有时可以只听到单一声音而听不到拍音.本文对实验中的各现象给出了解释,可以促进学生对驻波产生条件的理解.
2 金属管(杆)弯曲振动微分方程、边界条件及其求解
弯曲形变中,金属管(杆)内有一个平面保持无伸缩,称它为中面.设想金属管(杆)由许多和中面平行的矩形平片叠加而成.若处于中面以上的平片被拉伸,则处于中面以下的平片被压缩,反之亦然.如图1所示设金属管(杆)的轴向在x方向,弯曲方向在z方向.设元段ABCD形变为A′B′C′D′,其端面受正应力力矩作用,若端面倾斜角为φ,则该力矩,其中:IS为截面惯量矩,Y为杨氏模量.若是金属杆,则;若是金属管,则同时注意φ可用挠度w对x的导数来表示,考虑到元段端面切应力力矩应与正应力力矩平衡,可得元段所受的净力(沿z方向),再应用牛顿定律[1-2]即可得金属管(杆)弯曲振动的波动方程[3-5]
图1 金属管(杆)中的元段剖面图

其中:ρ为密度,β为阻尼常量,A0为横截面积.边界x=0和x=L端为自由端,端面上正应力力矩和切应力均为零,挠度函数w(x,t)需满足边界条件方程[4]

令w(x,t)=X(x)T(t),可解得Tω(t)=,关于X(x)的方程即为
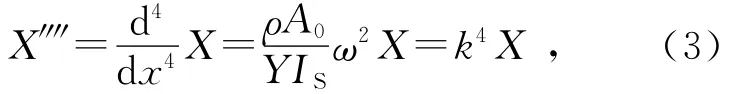
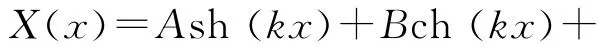

由边界条件方程(2)知,欲其解不是零解,k必须满足方程ch(kL)cos(kL)=1,该方程有无穷多个分立解.若把它的第n个解表示为βnπ,结果是β1=1.505 62,β2=2.499 75,βn≈(n+0.5)(n>2).相应的k用kn表示,kn=βnπ/L.由(3)式可得相应振动模式的固有频率为

对于金属杆,(5)式可变为
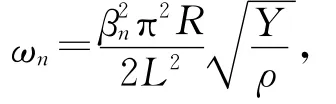
对于金属管,(5)式可变为

将kn代入边界条件方程可得Bn/An,加上归一化条件即可确定A0n,(3)式的基本解为

若令基频X1(x)=0,可得基频驻波波节点x11=0.224 157 52L,x12=0.775 842 48L.
金属管(杆)的任一自由振动均可表示为各模式基本解的线性叠加,即
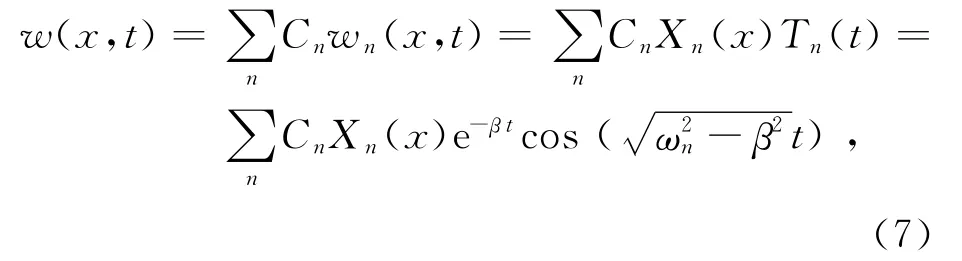
基本解Xn(x)又称振形函数,不同n的2个振形函数是相互正交[3].实验者手捏金属管(杆)和用锤敲击.捏持点将是振动能量的耗散点,捏持点为波节点的模式的振动能量将耗散得最慢.敲击点和敲击力度共同影响金属管(杆)的初始位移.因此捏持点和敲击位置、敲击力度及敲击(碰撞)时间共同影响着实验结果.设敲击引起的初始位移为
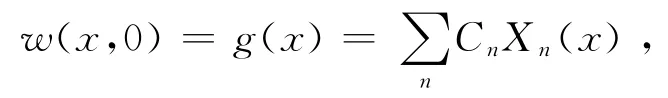
以Xm(x)乘以上式并在区间(0,L)进行积分,利用Xn(x)的正交归一性,可得

可见,哪一个模式的振形函数与敲击给出的初始位移覆盖得越多,(7)式的积分值就越大,该模式的振动就越显著.因此手持位置和敲击初位移一同起到选择振动模式的作用,改变手持位置和敲击初位移可以单独或共同改变所激发的模式,进而引起听到的声音的音调和音色发生改变.
3 对敲击金属管(杆)时出现拍音的解释
用手捏持距端点0.224L处且用橡胶锤敲击金属管(杆)的任一端点或中点,将使得基频模式振动得最为强烈,且时常听到拍音.
在推导元段端面正应力力矩时引入了截面惯量矩IS,它在数值上等于面密度为1的截面薄片绕中线的转动惯量.IS在式(5)式中也有所体现,说明刚体模型中的物理量影响着弯曲振动的结果.在实验中,金属管除沿长度方向的中轴作为1个主轴外,还有2个垂直于中轴的主轴,且这2个主轴相互正交.若金属管的结构是完全轴对称,则绕此两主轴转动的转动惯量相同.但实验中,绕此两正交主轴的转动惯量IS略有差别,使得2个偏振的基频模式的固有频率也略有差别,若对金属管的捏持点的连线平行于它的一个主轴,则沿另一个主轴方向敲击端点或中点将只激发在1个惯性主轴方向的弯曲振动,结果将只能听到1个频率的声音,否则2个偏振的基频模式都会被激发,这时就会听到拍音.若实验中听到了拍音,微微改变捏持点和敲击点的位置,再听听有无拍音,不断进行调整,就会发现在距端点0.224L的圆形截面圆周上存在两两互相成90°的4个点,相对捏持这样的点进行敲击就会听不到拍音而只有1种频率的声音了.
[1] 赵凯华,罗蔚茵.新概念物理教程·力学[M].北京:高等教育出版社,1995:215-222.
[2] 张三慧.大学物理学·力学[M].北京:清华大学出版社,1999:65-75.
[3] 郭敦仁.数学物理方法[M].北京:人民教育出版社,1965:213-223,240-252.
[4] 王矜奉,姜祖桐,石瑞大.压电振动[M].北京:科学出版社,1989:42-70.
[5] 路峻岭.物理演示实验教程[M].北京:清华大学出版社,2005:192-197.

