带准则参数的平差准则及其统一与解算
朱建军,田玉淼,陶肖静
1.中南大学测绘与国土信息工程系,湖南长沙410083;2.湖南省普通高等学校精密工程测量与形变灾害监测重点实验室,湖南长沙410083
1 引 言
经典的测量平差主要是以最小二乘作为平差准则,即以观测残差V的平方和最小(Φ=VTPV=min)作为确定平差参数X的估计准则,且准则函数只与观测残差有关。也可以使用由观测残差构成的一些其他准则,例如绝对值和最小准则(即一次范数最小准则,Φ=∑|V|=min)、稳健估计准则(Φ=∑ρ(V)=min)等。如果考虑平差参数的先验信息,也可构成广义最小二乘原理[1]。这些准则有一个共同特点,就是解可能不唯一(例如,一次范数平差就具有解非唯一性),但准则函数Φ相对于待估参数X的最小值是唯一的,平差参数的估计就是以函数Φ取到最小值为准则,即Φ函数的最小值是一个不随平差参数改变的唯一量。
近几十年以来,随着测量平差与数据处理理论的不断发展与进步,陆续出现了一些新的估计准则,例如,半参数估计的补偿最小二乘平差准则[2-3]、针对病态等不适定问题的正则化准则[4-5]、Vondrak滤波方法的平差准则[6-8]等。这些准则的特点是准则函数不但包含与观测值(残差)有关的部分,还包含有与观测值无关的部分(非观测部分),并且带有待定的参数。这些参数取不同值,将会有不同的准则函数极值,因而以准则函数取最小值为准则的平差将会得到不同的平差结果。关于如何利用这些准则进行平差,目前已经有大量的研究[9-21],并且得到了许多不同的方法。但对于同一模型的不同解算方法所得到的解之间有什么关系,如何进行比较等诸多问题却没有得到很好的解决。
对于测量中几种常见的平差模型,文献[22]将它们解的形式进行了统一。本文将主要针对不同平差准则的共性——平差准则带参数,从另一种思路出发,研究准则的统一及解算方法。为了叙述方便,将准则中出现的参数称为准则参数,把平差要求解的参数称为平差参数。下文将介绍各种带参数的平差准则及其统一,然后研究带参数平差准则下的平差解算方法,最后以实例验证有关解算方法的可行性。
2 带参数的平差准则及其统一
带参数的平差准则主要有半参数估计的补偿最小二乘平差准则、病态等不适定问题的正则化准则、Vondrak滤波方法的平差准则等。半参数估计的平差模型可表示为

式中,L为观测值;V为观测改正数;X为待定参数;A为系数矩阵;S为半参数。上述半参数模型的平差准则可写为[1-3]
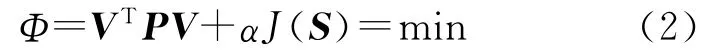
式中,J(S)是刻画非参数光滑性的一个函数。当采用自然样条函数来表述非参数的光滑性时,上述准则可变为[9-12]
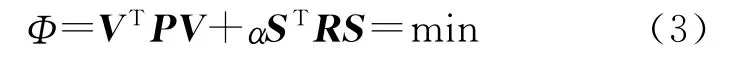
式中,R称为正则化矩阵,是一个对称非负定矩阵,描述了非参数的光滑性;α称为平滑参数,来平衡拟合和光滑程度,如果拟合程度较高,则其光滑程度较差,反之亦然。α为该准则中的准则参数,本身是待定的。
最小二乘的准则函数只与平差参数有关

而式(3)描述的半参数平差准则的准则函数则不但与平差参数有关,还与准则参数有关
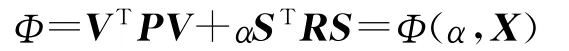
准则参数α取不同值,Φ=Φ(α,X)相对于平差参数X将会有不同的极值,因而会得到不同的解,但α到底取什么样的值最好,或取什么样的值最合理,目前并没有一个客观、统一的标准。上述半参数模型的解算方法有很多[1-3,9-12],但各种方法之间的解有什么关系,如何比较等还没有得到很好的解决。所以同一模型、同一套数据,不同人或不同方法会得到不同结果,甚至同一方法不同的人使用也会得到不同结果(如采用交叉核实法)。
病态等不适定问题的平差模型与经典平差类似,可表示为

正则化准则可表示为[4-5]
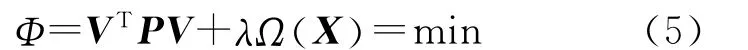

Vondrak滤波是一种用于测量数据序列滤波的方法,对于测量数据序列(xi,yi),i=1,2,…,N,xi为测量时刻,yi为对应于该时刻的测量值,可按下面准则进行滤波[6-8,20-21]
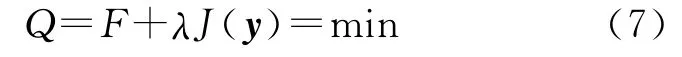

式中因子,起着平衡准则函数中两部分的作用。λ为该准则中的准则参数,其大小是待定的,λ选不同的值将会得到不同的结果。而Ω()X 应该取什么样的表达式是不确定的。目前大地测量领域中一般取



λ是平滑因子,它在平滑过程中调节着拟合度和平滑度之间的关系。一般说来,λ取值越大,滤波曲线的平滑程度越强;反之,平滑程度越弱。Vondark滤波的关键就是寻求一个平滑因子λ,得到一条介于对观测数据的绝对拟合和绝对平滑之间的曲线,λ就是上述准则中的准则参数。
上述3个平差准则,都可以统一于如下形式

式中,第1部分与最小二乘准则相同,由观测残差组成,描述的是观测信息。第2部分,对半参数而言,描述的光滑性,其中Z=S表示的是半参数,而RZ=R为正则化矩阵。对于不适定问题而言,第2部分描述的是稳定泛函,其中Z=X是待定的平差参数,而RZ=PX可以反映不同的泛函。对于Vondrak滤波而言,第2部分反映的也是光滑性,其中Z=y是数据的平滑值。RZ=R=BTB由式(8)确定。
对于准则参数λ,在半参数估计、病态等不适定问题和Vondrak滤波3种情况的意义都基本相同,就是起两部分的平衡作用。关于准则参数的确定目前已经开展了大量研究,提出了很多确定的方法,但各种准则参数的确定方法中有一个共同的不足就是:准则参数只是表示估计准则中观测相关部分及非观测部分之间平衡的一个模糊量,在客观上没有真实的值(真值)和物理(几何)含义,各种方法所确定的准则参数的数值表示的并不是同一个量的估计值,相互之间没有可比性。实际工作中可以依据不同经验或计算方法确定不同的值,并没有评价该参数是否最佳、是否合理的精度指标,其好坏主要靠模拟或其他方法来验证。
3 准则带参数时的一种通用平差方法——虚拟观测方法
式(10)表示的准则中的RZ矩阵在3种情况下都是对称非负定矩阵,作分解RZ=ATZAZ,令
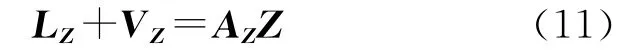
式中,LZ=0为虚拟观测,虚拟观测的方差用表示,则虚拟观测权为,这里当没有任何先验信息时,虚拟观测的权可取PLz=I,准则又可表示为

这是经典的最小二乘准则,准则参数λ相当于经典平差中的不同类观测的权比,这里定义为观测方差与描述非观测信息的虚拟观测方差的比,当没有任何先验信息时,可以按方差分量估计的方法确定。在上述准则下,半参数平差模型可以表示为
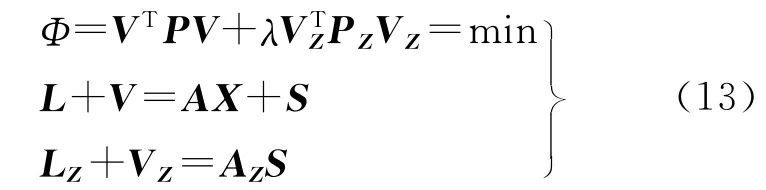
同样,正则化模型可表示为

Vondrak滤波模型可表示为
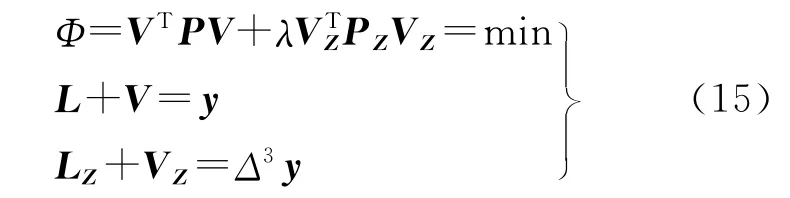
上述各模型,都用方差分量估计的方法进行最后解算,求得平差参数和准则参数。与原平差模型相比,上述各模型增加一组虚拟观测。虚拟观测大小为0,虚拟观测的误差方程系数由原准则中的正则化矩阵确定,虚拟观测的权由先验信息确定或用方差分量估计的方法确定。整个平差都使用上面的准则,按经典平差方法,利用经典平差程序进行平差。
虚拟观测方法在数据处理中的应用研究,包括利用虚拟观测计算附有限制条件的间接平差[23]和求解附有不等式约束的平差模型[24],利用虚拟观测值来确定岭估计的岭参数[25],结合虚拟观测确定半参数、Vondark滤波的平滑因子[12,20],利用虚拟观测值引入半参数回归模型的约束信息[26]等,都可以得到与传统方法等价或较优的计算结果。这里将准则带参数的平差方法,包括半参数估计、病态等不适定问题和Vondrak滤波等,用虚拟观测法统一成同一种形式。每一种准则带参数的平差方法都可以通过这种统一的形式直接求解。
上述平差的所有参数和过程都是客观的,平差结果取决于平差问题和实际观测,不存在主观因素的干预,因此不会因为人为因素而得到不同的平差结果。
4 算 例
用虚拟观测方法求解半参数模型和Vondrak滤波可行性,文献[12,20]已经有了研究,这里选择不适定问题,研究虚拟观测解法的可行性。以GPS快速定位为例,数据来自中南大学GPS基线场的超短基线,WGS-84坐标下基线向量为6.447m、0.630m、3.543m,长度为7.383m,历元间隔5s,基线初始值由每组历元第一个历元CA码确定。
GPS快速定位时,误差方程高度病态。本例以文献[4]提出的方法构建正则化准则中的正则矩阵,分别用最小二乘方法(LS)、文献[4]提出的方法(WZJ)及本文的虚拟观测方法(VO)3种方法平差。模糊度固定时,使用3种方法各自的协方差阵,通过Lambda法计算。计算以下3种情况的数据:连续5个历元(共计算50组)、连续10个历元(共计算50组)、连续15个历元(共计算50组)。
由于在该基线上有很长时间的观测数据,可以用静态基线方法计算并固定各GPS观测的模糊度。本次计算中,以固定了的模糊度作为模糊度真值,以模糊度固定后基线的解作为基线向量的真值。上述3种情况计算的结果与上述真值比较,得到解的偏差(相减,取绝对值,相应50组取平均)。结果列于表1、表2和表3,模糊度固定正确的概率列于表4。图1显示的是50组计算结果中,基线浮点解误差的范数变化情况,其中增加了每组12个历元的计算结果,以更好地说明图形随历元增加的变化趋势。
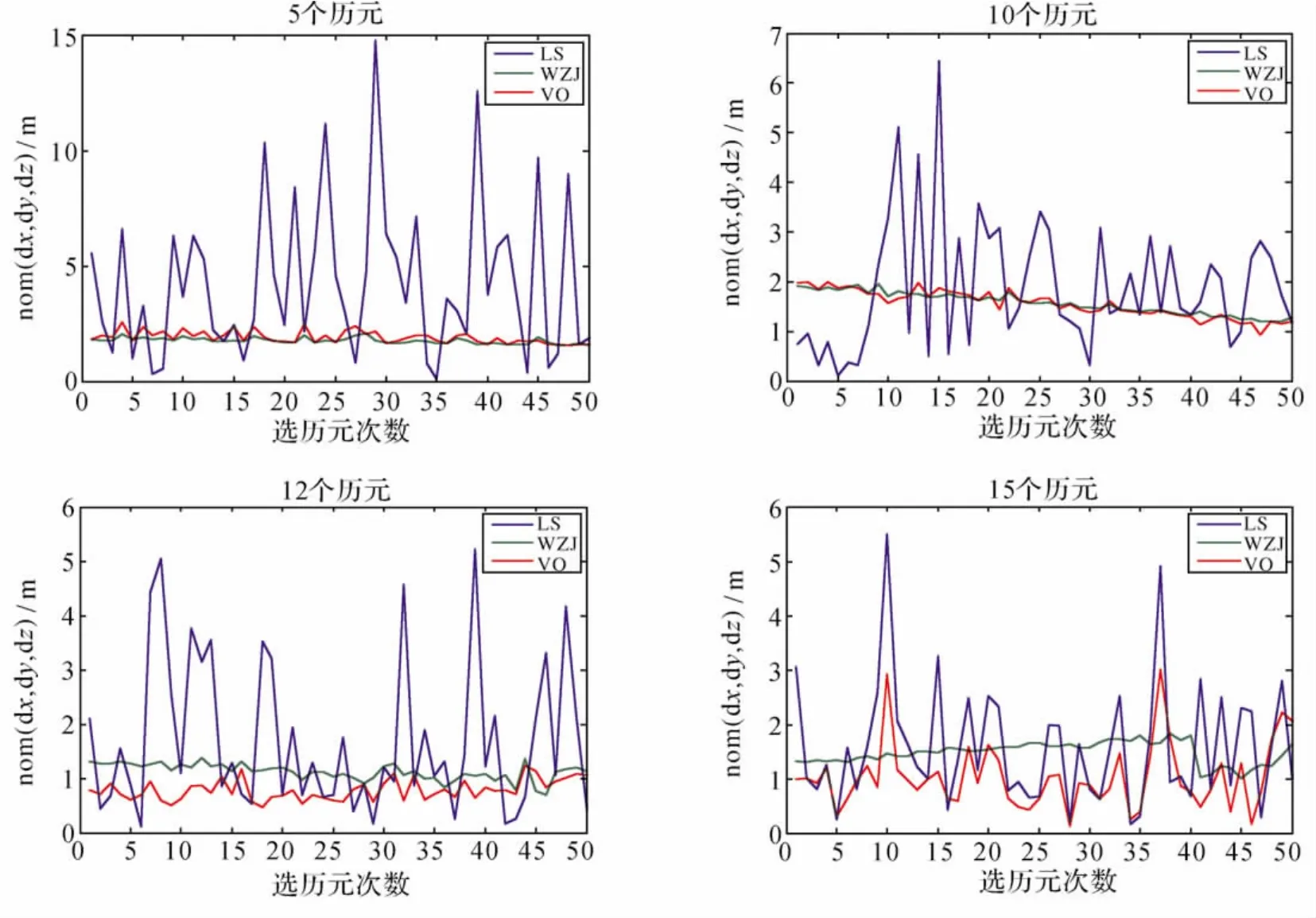
图1 连续几个历元,共计算50组求得的浮点解偏差Fig.1 The biases of the differences between the real values and the float solutions,computed from 50series

表1 连续5个历元,共计算50组求得的浮点解平均偏差Tab.1 The mean biases of the differences between the real values and the float solutions,computed from 50series and each using 5epochs m

表2 连续10个历元,共计算50组求得的浮点解平均偏差Tab.2 The mean biases of the differences between the real values and the float solutions,computed from 50series and each using 10epochs m

表3 连续15个历元,共计算50组求得的浮点解平均偏差Tab.3 The mean biases of the differences between the real values and the float solutions,computed from 50series and each using 15epochs m
利用上述浮点解,进行模糊度固定,其成功率列于表4。

表4 固定模糊度的成功率Tab.4 The success rate of the ambiguities fixed
WZJ方法是不管观测实际情况如何都取α=1,这实际上是一种强压缩估计,相当于使用岭估计时总是取较大的岭参数。当误差较大,初始坐标较精确时,这种方法对误差进行了较大的压缩,而对平差值的压缩由于初始坐标较精确产生的偏差很小,因而能取到比较好的效果,但如果初始值难以保证精度时,则会由于对平差值的强压缩而产生较大的系统偏差。表1是5历元计算结果,5历元的解误差较大,WZJ方法可对误差进行较大的压缩,初始值由伪距观测计算得到,在短基线情况下精度较好,因此,其浮点解取得了较好的结果。但由于它对平差值的压缩较大,初始值也可能仍没有达到WZJ方法需要的理想精度[14],由此引起的系统性偏差(有偏估计中的偏量)也比较大,因此,在进行模糊度固定时就难以取到好的结果,在本次试验中,尽管WZJ方法浮点解取得了比较好的结果,但其模糊度固定的效果却不是很理想(见表4)。
随着历元的增多,WZJ方法得到的浮点解精度不会明显提高,而普通最小二乘法的浮点解精度却得到了很大改善,此时虚拟观测值法也会像最小二乘一样,浮点解精度不断提高,它的浮点解精度和正确固定模糊度的概率要高于最小二乘。
可见,虚拟观测法解算准则带参数的平差模型是可行的,综合考虑浮点解精度和模糊度固定解算结果,虚拟观测法解算带参数的平差模型有明显优势。
5 结 论
(1)半参数方法、正则化方法等平差准则中带有待定参数的平差方法都可以用统一的带参数的平差准则来描述。各种不同方法的差别主要在于描述非观测信息的矩阵RZ的形式和计算时所采用的方法,其中不同的RZ表示的非观测信息的物理意义不同。
(2)准则带参数的平差模型可用虚拟观测方法来解算。准则参数实际表示的是虚拟观测方差与观测方差的一个比值,如果没有先验信息确定该比值,可用方差分量估计的方法确定。
(3)算例表明,对于正则化问题,虚拟观测法解算准则带参数的平差模型有明显优势,虚拟观测法解算准则带参数的平差模型是可行的。
[1] CUI Xizhang,YU Zongchou,TAO Benzao,et al.Generalized Surveying Adjustment[M].Wuhan:Publishing House of Wuhan Technical University of Surveying and Mapping,2001.(崔希璋,於倧俦,陶本藻,等.广义测量平差[M].武汉:武汉测绘科技大学出版社,2001.)
[2] CHAI Genxiang,HONG Shengyan.Semiparametric Regression Model[M].Hefei:Anhui Education Press,1995.(柴根象,洪圣岩.半参数回归模型[M].合肥:安徽教育出版社,1995.)
[3] DING Shijun.Survey Data Modeling and Semiparametric Estimating[D].Wuhan:Wuhan University,2005.(丁士俊.测量数据的建模和半参数估计[D].武汉:武汉大学,2005.)
[4] WANG Zhenjie.Research on the Regularization Solutions of Ill-posed Problems in Geodesy[D].Wuhan:Wuhan University,2003.(王振杰.大地测量中不适定问题的正则化解法研究[D].武汉:武汉大学,2003.)
[5] XU Peiliang,FUKUDA Y,LIU Yumei.Multiple Parameter Regularization:Numerical Solutions and Applications to the Determination of Geopotential from Precise Satellite Orbits[J].Journal of Geodesy,2006,80(1):17-27.
[6] VONDRAK J.A Contribution to the Problem of Smoothing Observational Data[J].Bulletin of the Astronomical Institute of Czechoslovakia,1969,20(6):349-355.
[7] VONDRAK J.A Contribution to the Problem of Smoothing Observational Data II[J].Bulletin of the Astronomical Institute of Czechoslovakia,1977,28(2):84-89.
[8] ZHENG D W,ZHONG P,DING X L,et al.Filtering GPS Time-series Using a Vondrak Filter and Cross-validation[J].Journal of Geodesy,2005,79:363-369.
[9] DING Shijun,TAO Benzao.Semiparametric Regression and Adjustment Models[J].Journal of Geodesy and Geodynamics,2003,23(4):111-114.(丁士俊,陶本藻.半参数回归与平差模型[J].大地测量与地球动力学,2003,23(4):111-114.)
[10] PAN Xiong.The Estimation Theory and Application Research in Semi-parametric Model[D].Wuhan:Wuhan University,2005.(潘雄.半参数模型的估计理论及其应用[D].武汉:武汉大学,2005.)
[11] WU Yun,SUN Haiyan,MA Xuezhong.Semiparametric Regression with Cubic Spline[J].Geomatics and Information Science of Wuhan University,29(5):398-401.(吴云,孙海燕,马学忠.半参数估计的自然样条函数法[J].武汉大学学报:信息科学版,2004,29(5):398-401.)
[12] ZHU Jianjun,FENG Guangcai,DAI Wujiao.A Quasi Observation Approach for Semi-parameter Regression[J].Geotechnical Investigation &Surveying,2006,(9):54-57.(朱建军,冯光财,戴吾蛟.半参数模型解算的一种虚拟观测法[J].工程勘察,2006,(9):54-57.)
[13] WANG Zhenjie,OU Jikun,LIU Lintao.A Method for Resolving Ill-conditioned Problems:Two-step Solution[J].Geomatics and Information Science of Wuhan University,2005,30(9):821-824.(王振杰,欧吉坤,柳林涛.一种解算病态问题的方法:两步解法[J].武汉大学学报:信息科学版,2005,30(9):821-824.)
[14] WANG Zhenjie,OU Jikun,LIU Lintao.Investigation on Solutions of Ill-conditioned Problems in Rapid Positioning Using Single Frequency GPS Receivers[J].Acta Geodaetica et Cartographica Sinica,2005,34(3):197-201.(王振杰,欧吉坤,柳林涛.单频GPS快速定位中病态问题的解法研究[J].测绘学报,2005,34(3):197-201.)
[15] SHEN Yunzhong,XU Houze.Spectral Decomposition Formula of Regularization Solution for Ill-posed Equation[J].Journal of Geodesy and Geodynamics,2002,22(3):10-14.(沈云中,许厚泽.不适定方程正则化算法的谱分解式[J].大地测量与地球动力学,2002,22(3):10-14.)
[16] XU Peiliang,SHEN Yunzhong,FUKUDA Y,et al.Variance Component Estimation in Linear Inverse Illposed Models[J].Journal of Geodesy,2006,80:69-81.
[17] ZENG Qunyi,OU Jikun.Study on Application of Genetic Algorithms in Solving Ill-conditioned Equation[J].Journal of Geodesy and Geodynamics,2003,23(3):93-97.(曾群意,欧吉坤.用遗传算法解算病态方程[J].大地测量与地球动力学,2003,23(3):93-97.)
[18] GUI Qingming.A New Selection Method for Ridge Parameter[J].Engineering of Surveying and Mapping,1997,6(1):14-19.(归庆明.选取岭参数的一个新方法[J].测绘工程,1997,6(1):14-19.)
[19] ZHU Jianjun.A New Algorithm on the Ridge Estimator[J].Journal of Geomatics,1997,(3):22-25.(朱建军.岭估计的一种新的算法[J].测绘信息与工程,1997,(3):22-25.)
[20] ZHOU Xiaowei,DAI Wujiao,ZHU Jianjun.A Filtering Method of Vondrak Based on the Helmert Type Variance Component Estimation[J].Geotechnical Investigation &Surveying,2007(6):42-45.(周晓卫,戴吾蛟,朱建军,等.基于Helmert方差分量估计的Vondrak滤波方法[J].工程勘察,2007(6):42-45.)
[21] CAO Mengcheng,ZHU Jianjun,ZOU Zhengrong,et al.Application of Vondrak Filtering in Cycle-slip Detecting and Repairing[J].Geotechnical Investigation &Surveying,2006(10):53-56.(曹梦成,朱建军,邹峥嵘,等.Vondrak滤波在周跳探测与修复中的应用[J].工程勘察,2006(10):53-56.)
[22] OU Jikun.Uniform Expression of Solutions of Ill-posed Problems in Surveying Adjustment and the Fitting Method by Selection of the Parameter Weights[J].Acta Geodaetica et Cartographica Sinica,2004,33(14):282-288.(欧吉坤.测量平差中不适定问题解的统一表达与选权拟合法[J].测绘学报,2004,33(14):282-288.)
[23] ZHAO Haitao,GUO Guangli.The Virtual Observation Algorithm with Restriction Condition Parameter Adjustment[J].Science of Surveying and Mapping,2008,33(2):33-37.(赵海涛,郭广利等.附有限制条件间接平差的虚拟观测算法[J].测绘科学,2008,33(2):33-37.)
[24] OUYANG Wensen,ZHU Jianjun.Expanding of Classical Surveying Adjustment Model[J].Acta Geodaetica et Cartographica Sinica,2009,38(1):12-15.(欧阳文森,朱建军.经典平差模型的扩展[J].测绘学报,2009,38(1):12-15.)
[25] DAI Wujiao,FENG Guangcai,ZHU Jianjun.A Method for Selecting Ridge Parameter Based on Helmert Variance Components Estimation[J].Journal of Geodesy and Geodynamics,2006,26(4):30-33.(戴吾蛟,冯光财,朱建军.一种基于Helmert方差分量估计的岭参数确定方法[J].大地测量与地球动力学,2006,26(4):30-33.)
[26] LE Kejun,QIU Bin,ZHU Jianjun.Semi-parametric Regression Model Constrained with Priori Information and Its Virtual Observations Solution[J].Journal of Geodesy and Geodynamics,2008,28(6):107-111.(乐科军,邱斌,朱建军.具有先验信息约束的半参数回归模型及其虚拟观测值解法[J].大地测量与地球动力学,2008,28(6):107-111.)

