粗差探测与识别统计检验量的比较分析

郭建锋，赵 俊

1.信息工程大学理学院，河南郑州450001；2.中国科学院测量与地球物理研究所，湖北武汉430077

1 引 言

为保证测量成果达到设计要求，在完成实测任务后，必须进行测量数据的质量分析。大量研究表明，粗差仅仅占到观测量总数的1%至10%左右。粗差的存在往往对最小二乘（least－squares，LS）估计造成不良的影响，即LS估计的抗差性（robustness，又译为稳健性）非常差［1－12］。

对于工程技术与应用领域而言［2］，抗差性可以理解为统计推断中的敏感度分析理论（或者称为扰动分析、稳定性分析理论）。换言之，抗差性，即估计量抵御粗差影响的能力，表现为平差结果对观测异常的敏感程度［5］。拟合优度检验［5－7］是检验平差成果的一项重要指标。因此，通过对拟合优度检验量进行敏感度分析构造探测与识别观测异常的统计量，具有显著的物理意义。

在粗差探测法中，假定随机模型能够客观反映观测量之间的（相对）精度及统计相关性，把粗差问题归结为函数模型与实际模型的偏离。如果拟合优度检验结果不显著，说明在一定显著性水平上，平差成果达到了要求，可以采纳；否则就表明当前的函数模型不能准确描述观测量之间或观测量与未知参数之间的物理或者几何关系［6，13］。需要指出的是，拟合优度检验虽然能够检验出粗差的存在与否，但却不能探测和准确定位有几个观测量以及具体是哪几个观测量受到了多大量级的粗差污染［13，15］。

在粗差的探测与识别中，通常采用正态检验、学生氏t检验以及τ检验等，而构造相应的统计检验量既可基于局部敏感度指标，亦可基于LS残差。本文对实施粗差探测与识别的统计检验量进行了比较分析，得到如下结论：① 相关观测情形，局部敏感度指标比LS残差的检验功效大，若单位权中误差精确已知，宜采用基于标准化局部敏感度指标的正态检验；② 单位权中误差未知时，τ检验理论本身存在固有缺陷，而学生氏t检验或将造成“纳伪”错误的增加，较为稳妥的方案是仍然采用正态检验，但将标准化局部敏感度指标中的单位权中误差以其抗差LMS（least median of squares）估计代替。

2 模型描述

考虑如下线性Gauss－Markov模型［5－7］

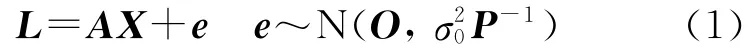
式中，A为n×u（n－u＞1）列满秩设计阵；X为u×1未知参数向量；L为n×1观测向量；e为相应的误差（噪声）向量，其方差－协方差阵为这里对称正定阵P为观测量的先验权阵，而通常称为单位权方差因子。

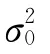
基于LS原理，可得到模型（1）中未知参数的LS估计为［5－7］

相应的残差向量为

式中，R＝I－A（ATPA）－1ATP以矩阵形式反映平差结构，是质量的全面度量，称为平差因子阵［12］。

容易验证平差因子阵R幂等，并具以下有用性质

基于此，LS残差的加权平方和Ω＝VTPV亦可表示为［13－16］

3 基于敏感度分析的统计量

3.1 标准化局部敏感度指标

将LS残差的加权平方和对第i个观测量li进行微分，得到［13－14］

式中，hi表示第i个分量为1，其余分量皆为0的n维单位向量。

显然，∂Ω／∂li衡量的是Ω对第i个观测值的扰动的敏感程度。注意到

因此统计量

可用于检验Ω对第i个观测量的扰动是否“敏感”。

根据已知数据可以计算出w统计检验量的取值，其绝对值越大，表明Ω对第i个观测量的扰动越“敏感”，故而li受到粗差污染的可能性就越大。因此，称为第i个观测量的标准化局部敏感度指标［13－14］。

应该指出的是，这里的wi即为可靠性理论中Baarda［17］导出的w统计检验量。

3.2 外部学生化局部敏感度指标

通过对局部敏感度指标进行标准化，可以有效消除量纲的影响，这对于多源数据融合的质量控制问题意义尤为重要。然而，得到标准化局部敏感度指标的前提是先验单位权中误差精确已知，否则就无法利用w统计量进行假设检验。

在测量实践中，先验单位权中误差往往未知［5－7，12］。为此，本文提出如下服从自由度为nu－1的学生氏分布的统计检验量

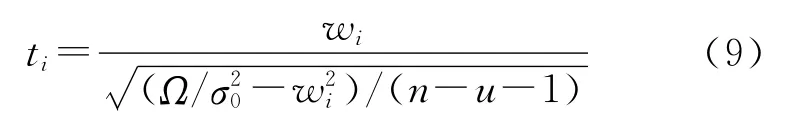
当存在多个粗差时，LS残差的加权平方和Ω往往偏大。由定义不难知道，这或将导致外部学生化局部敏感度指标普遍偏小，进而造成“纳伪”错误的增加。因此，基于外部学生化局部敏感度指标探测和识别粗差潜在一定的风险。

3.3 内部学生化局部敏感度指标

单位权中误差未知时，还可通过构造统计量进行粗差的探测与识别，这里为平差模型式（1）中的验后单位权方差因子。称为内部学生化局部敏感度指标。

统计量式（10）亦可表达为服从学生氏分布的统计量ti的函数，即

Thompson将统计量τi服从的分布称为自由度为n－u的τ分布［18］。在测量质量控制中，τ检验是应用最为广泛的统计量之一［5，18－24］。

Beta分布的一个显著特点是其仅仅在单位区间（0，1）内取值［5］，于是得到

注意到关系式

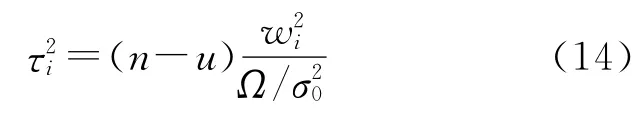
有

式（15）表明，服从τ分布的统计量之绝对值存在上界，而且该上界仅取决于该统计量的自由度。

4 基于残差的统计量

在经典测量平差中仅涉及独立等权观测数据，这种情况下，线性最小二乘平差理论中最基本的关系式ATPV＝O退化为

因此，在传统的粗差探测与识别中，均以残差作为对象研究问题。

4.1 标准化残差

若先验单位权中误差精确已知，可构造如下称为标准化残差的统计量［17］

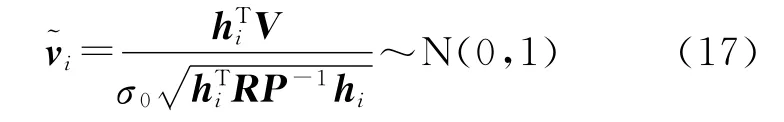
探测和识别粗差。

及

式中，ri表平差因子阵R的第i个对角元。

依据Cauchy－Schwarz不等式，有

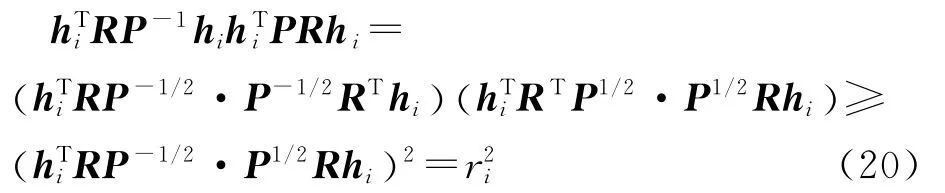
由此得到

一个统计检验量的检验功效是显著性水平和非中心化参数的单调增函数［25］，因此统计量wi比标准化残差的检验功效要大，或者等价的，比统计量的检验功效要大。

事实上，统计量Ti为一致最大检验功效统计量［24］。也就是，在给定的显著性水平上，利用Ti（或wi）进行假设检验犯“纳伪”错误的概率比使用任何其他的统计量都要小。

相反，若事先指定显著性水平和检验功效，统计量所对应的非中心化参数将唯一确定，由式（21）立即可知：一致最大检验功效统计量Ti（或wi）对应的最小可探测粗差指标［16－17，25］不会超过统计量（或标准化残差），换言之，一致最大检验功效统计量Ti（或wi）较统计量（或）对粗差更敏感。

由于相关观测情形下统计量wi比标准化残差的检验功效要大，而在独立观测情形二者则完全一致，因此建议采用统计检验量wi进行粗差的探测和识别。

4.2 外部学生化残差

先验单位权中误差未知时，可构造如下统计检验量

这称为外部学生化残差［4］。

根据关系式RP－1＝RP－1RT，容易验证矩阵

为幂等阵，注意到

综合上款，二次型

服从自由度为n－u－1的χ2分布［5］。

由于

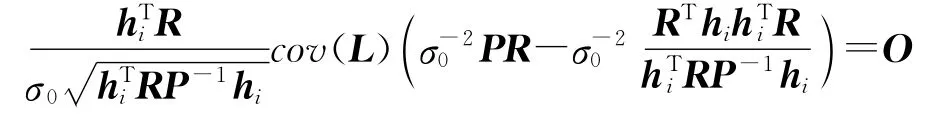
依据正态随机向量的线性组合与其二次型相互独立的判定定理［5］可知，标准化残差与相互统计独立，因而，外部学生化残差服从自由度为n－u－1的学生氏分布。

与外部学生化局部敏感度指标类似，当存在多个粗差时，统计量或潜在一定的风险。

4.3 内部学生化残差

若单位权中误差未知，还可构造如下称之为内部学生化残差的统计量［26］

进行粗差的探测与识别。

由于

根据正态随机向量的两个二次型相互独立的判定定理［5］与相互统计独立。因此，统计量

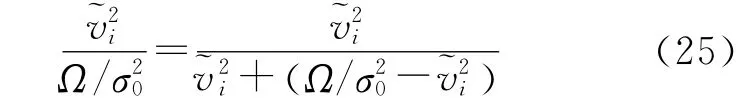
服从自由度分别为1／2、（n－u－1）／2的Beta分布。进而，内部学生化残差统计量~τi服从自由度为n－u的τ分布［18］。

及

于是，当扰动量δi趋于无穷大时，第i个内部学生化残差的绝对值之极限为

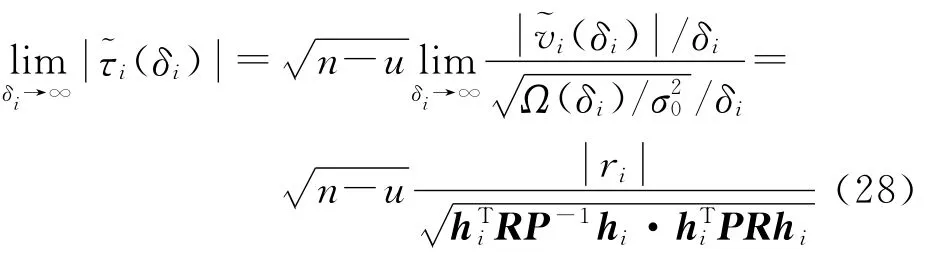
这个结果由Baselga［20］给出。

若顾及不等式（20），还可以进一步求出上述极限值的上界

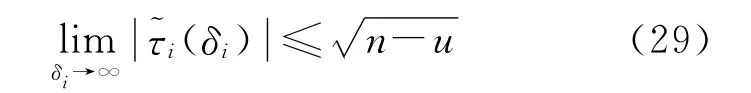
式（29）再次验证了这样一个事实，即τ检验理论本身确乎存在缺陷。因而，使用τ统计量探测和识别粗差存在一定风险。

5 结论与建议

（1）若单位权中误差精确已知，可采用正态检验。w统计量反映的是χ2拟合优度检验量对观测值扰动的敏感程度，因而具有明确的物理意义；作为一致最大检验功效统计量，对于给定的显著性水平和检验功效，Ti＝（或wi）能够探测出量级最小的粗差。

因此，进行正态检验时，w统计量为首选，标准化残差次之。

（2）若σ未知，可采用τ检验或t检验。τ检验理论本身固有缺陷；而存在多个粗差时，t检验或将造成“纳伪”错误的增加，亦存在一定的风险。

从检验功效的角度考虑，无论进行τ检验抑或t检验，均建议采用基于局部敏感度指标的检验量。

（3）Robust正态检验。由于τ检验和t检验均存在一定缺陷，因此尚需对单位权方差因子未知时的粗差探测与识别作进一步的讨论。

一种较为稳妥的解决方案是，采用具有明确物理意义的w统计量，而统计量中的未知参数σ则以其抗差LMS估计代替之［1－3，12－15］。即以

代替统计量wi中的先验单位权中误差σ。

将基于修正的w统计量的检验称为Robust正态检验。从数学上说，修正的w统计量并不严格服从正态分布。然而经验表明，该统计量具有较强的抗差性，当冗余观测较多时尤为如此［1－3，12－15］。

［1］ HUBER P J，RONCHETTI E M.Robust Statistics［M］.2nd ed.New York：Wiley，2009.

［2］ HAMPEL F R，RONCHETTI E M，ROUSSEEUW P J，et al.Robust Statistics：The Approach Based on Influence Functions［M］.New York：Wiley，1986.

［3］ ROUSSEEUW P J，LEROY A M.Robust Regression and Outlier Detection［M］.New York：Wiley，1987.

［4］ CHATTERJEE S，HADI A S.Sensitivity Analysis in Linear Regression［M］.New York：Wiley，1988.

［5］ KOCH K R.Parameter Estimation and Hypothesis Testing in Linear Models［M］.2nd ed.Berlin：Springer－Verlag，1999.

［6］ LEICK A.GPS Satellite Surveying［M］.3rd ed.New York：Wiley，2004.

［7］ WOLF P R，GHILANI C D.Adjustment Computations：Statistics and Least Squares in Surveying and GIS［M］.3rd ed.New York：Wiley，1997.

［8］ ZHOU Jiangwen.Classical Theory of Errors and Robust Estimation［J］.Acta Geodaetica et Cartograghica Sinica，1989，18（2）：115－120.（周江文.经典误差理论与抗差估计［J］.测绘学报，1989，18（2）：115－120.）

［9］ OU Jikun.Quasi－accurate Detection of Gross Errors（QUAD）［J］.Acta Geodaetica et Cartograghica Sinica，1999，28（1）：15－20.（欧吉坤.粗差的拟准检定法（QUAD法）［J］.测绘学报，1999，28（1）：15－20.）

［10］ SONG Lijie，YANG Yuanxi.Comparison between Data Snooping and LEGE［J］.Acta Geodaetica et Cartograghica Sinica，1999，28（4）：295－300.（宋力杰，杨元喜.均值漂移模型粗差探测法与LEGE法的比较［J］.测绘学报，1999，28（4）：295－300.）

［11］ LI Xinna，GUI Qingming，XU Apei.Besian Method for Detection of Gross Errors Based on Classification Variables［J］.Acta Geodaetica et Cartograghica Sinica，2008，37（3）：355－360.（李新娜，归庆明，许阿裴.基于识别变量的粗差探测的Bayes方法［J］.测绘学报，2008，37（3）：355－360.）

［12］ ZHOU Jiangwen，HUANG Youcai，YANG Yuanxi，et al.Robust Least Squares Method［M］.Wuhan：Huazhong University of Science and Technology Press，1997.（周江文，黄幼才，杨元喜，等.抗差最小二乘法［M］.武汉：华中理工大学出版社，1997.）

［13］ GUO Jianfeng.Theory of Model Errors and its Applications in GPS Data Processing［D］.Wuhan：Institute of Geodesy and Geophysics of Chinese Academy of Sciences，2007.（郭建锋.模型误差理论若干问题研究及其在GPS数据处理中的应用［D］.武汉：中科院测量与地球物理研究所，2007.）

［14］ GUO J F，OU J K，WANG H T.Quasi－accurate Detec－tion of Outliers for Correlated Observations［J］.Journal of Surveying Engineering，2007，133（3）：129－133.

［15］ GUO J K，OU J K，WANG H T.Robust Estimation for Correlated Observations：Two Local Sensitivity－based Downweighting Strategies［J］.Journal of Geodesy，2010，84（4）：243－250.

［16］ GUO J K，OU J K.Variation Characteristics of MDBs in Robust Estimation［J］.AllgVerm－Nachr，2010，117（2）：49－52.

［17］ BAARDA W.A Testing Procedure for Use in Geodetic Networks［J］.Netherlands Geod Comm Publ on Geod，1968，2（5）：1－97.

［18］ POPE A J.The Statistics of Residuals and the Detection of Outliers［R］.Rockville：NOAA Technical Report，Nos 65，NGS 1，1976.

［19］ KOK J J.On Data Snooping and Multiple Outlier Testing［R］.Rockville：NOAA Technical Report，Nos NGS 30，1984.

［20］ BASELGA S.Critical Limitation in Use ofτTest for Gross Error Detection［J］.Journal of Geodesy，2007，133（2）：52－55.

［21］ CROSS P A，PRICE D R.A Strategy for the Distinction between Single and Multiple Gross Errors in Geodetic Networks［J］.Manuscr Geod，1985，10（3）：172－178.

［22］ DING X，COLEMAN R.Multiple Outlier Detection by Evaluating Redundancy Contributions of Observations［J］.Journal of Geodesy，1996，70（8）：489－498.

［23］ SNOW K B，SCHAFFRIN B.Three－dimensional Outlier Detection for GPS Networks and Their Densification via the BLIMPBE Approach［J］.GPS Solutions，2003，7（2）：130－139.

［24］ KARGOLL B.On the Theory and Application of Model Misspecification Tests in Geodesy［D］.Bonn：University of Bonn，2007.

［25］ TEUNISSEN P J G.Quality Control in Integrated Navigation Systems［C］∥Proceedings of the IEEE PLANS90，Nevada：IEEE，1990：158－165.

［26］ COOK R D.Detection of Influential Observations in Linear Regression［J］.Technometrics，1977，19（1）：15－18.