多维平差问题粗差的局部分析法

孙海燕，黄华兵，王喜娜

武汉大学测绘学院，湖北武汉430079

1 引 言

由于仪器、测量环境和观测人员等方面的原因，观测值有时会包含粗差。如果观测值中含有粗差，采用最小二乘法进行平差时，粗差的存在不可避免会对平差结果产生不利影响，甚至导致错误的结果。这个结论已经得到理论上的证明和实践的验证。

现在已经有许多方法来消除或减弱粗差的影响。这些方法通常分为两类。一类是依据统计学原理对粗差进行探测与定位并将其剔除，这方面的研究以文献［1］的粗差探测法为代表。另一类是稳健估计（又称抗差估计），这种方法不需要对粗差进行定位与剔除，而是选择适当的估计方法（如L1范数最小估计、M估计等），使得估计结果不受或少受粗差的影响。在实际计算中，这些方法大都是通过给含有粗差的观测值一个较小的权，从而减小该观测值在平差中的作用。常用的方法主要是选权迭代法，如丹麦法、文献［2］提出的验后方差估计法和文献［3—5］提出的IGG方案。实际上这两类方法都依赖于通过平差计算得到的改正数，而含有粗差的观测值并不一定得到较大的改正数，因而有时会造成误判。也有研究人员从真误差出发，提出了有益的方法。文献［6］提出了多维粗差同时定位定值法（LEGE法），文献［7］提出了粗差的拟准检定法（QUAD法）。使用LEGE法和QUAD法都需要进行平差计算，同样也受到改正数的影响，比如作为LEGE法判断依据的单位权中误差是改正数的函数，QUAD法选择拟准观测的指标也是改正数的函数。

实际上，在处理粗差之前应该分析多维平差问题中是否存在一类观测值，出现在其中的粗差是不可发现或无法定位的。粗差处理方法不能有效处理这类粗差，故其对平差结果可能会产生较大影响。能否发现某个观测值中的粗差，或者消除或减弱其影响，不仅取决于多余观测数等全局性指标，而且与粗差出现的位置有关。关于粗差所处位置对粗差处理的影响，文献［8］曾提出杠杆观测的概念，指出不论实际误差如何，杠杆观测只得到低改正，这使得杠杆观测含有的粗差比其他位置的粗差难于发现。

综上所述，本文试图建立一种局部的粗差分析方法，不依赖于平差计算和改正数，确定出现在某个位置的粗差是否可以被发现和定位，并且在此基础上给出一种粗差探测方法。

2 局部分析法

在讨论局部分析法之前，先分析一个水准网，如图1所示。

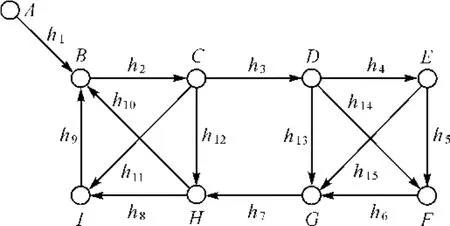
图1 水准网Fig.1 Leveling network

图1中，A点高程已知，其余8点高程待求，观测值等精度，观测方向如箭头所示。

无论观测值取何值，h1的改正数为0，h3和h7的改正数大小相等。

假设水准网中只有一个粗差。若h1含有粗差，则根据改正数不可能发现粗差。若粗差出现在h3或h7上，则必然导致错误。由于h3和h7的改正数大小相等，结果只能是h3和h7都有粗差或者都没有粗差，这两种结果都与实际情况不符。

从图1水准网的分析可以看出，粗差能否被正确处理与其位置密切相关。基于此，本文提出多维平差问题粗差的局部分析法。

2.1 局部分析法原理

局部分析法的主要思路是从局部考察一个观测值，讨论平差问题能否容忍出现在其中的粗差。具体做法是将局部化作一个一维问题，再应用一维问题粗差分析的结论进行讨论。

首先，给出一维问题粗差分析的结论。设对一个真值未知的被观测量进行m次观测。m＝1时，观测值的真值未知，故其含有的粗差是不可发现的。m＝2时，两个观测值之差的理论值为0，比较观测值即可确定二者是否含有粗差，但无法确定谁含有粗差。m≥3时，根据稳健估计中位数法，如果观测值中含有k（0＜k＜m／2）个粗差，那么中位数是正常观测值，故粗差可以全部定位；如果含有k（k≥m／2）个粗差，则不能定位。

对于多维平差问题，比较一个被观测量的观测值与其组合观测，可发现观测值和组合观测是否含有粗差。组合观测定义为：设s为多维平差问题的一个被观测量，其观测值为L，如果存在其他被观测量s1、s2、…、sm（对应观测值为L1、L2、…、Lm）的函数f满足f（s1，s2，…，sm）＝s，则称f（L1，L2，…，Lm）为s的组合观测。另外，一维问题的粗差分析要求观测值是误差独立的，所以在多维平差问题的粗差分析中使用的组合观测也应当是误差独立的，即要求所有组合观测两两之间没有公共观测值。根据组合观测确定误差独立组合观测以后，即可将误差独立组合观测与观测值看做对被观测量的重复观测，从而可以应用一维问题的结论分析被观测量。

设s为多维平差问题的一个被观测量，其观测值为L。记s的误差独立组合观测数为m1，包含观测值和误差独立组合观测的总独立观测数为m2。根据m1的取值讨论如下：

（1）m1＝0时，m2＝1，由一维问题结论可知观测值含有的粗差是不可发现的。

（2）m1＝1时，m2＝2，可以发现粗差但不能定位。

（3）m1≥2时，m2≥3，如果被观测量k（0＜k＜m2／2）个独立观测含有粗差，那么可以定位粗差。

局部分析法的关键是计算被观测量的误差独立组合观测数。下面给出根据多维平差问题函数模型确定误差独立组合观测数的一般方法。

2.2 误差独立组合观测

多维平差问题的函数模型为

可从B中选取t行组成矩阵B2（t×t），使得B2可逆，余下的n－t行构成矩阵B1。按此选法可得对应的和d2，于是式（1）可写为

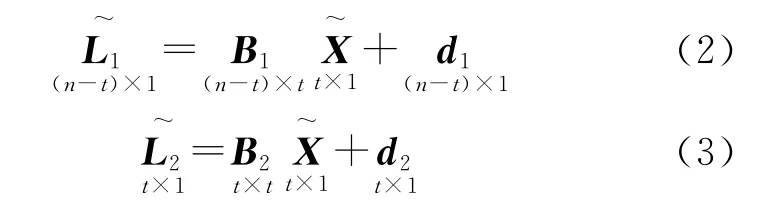
B2可逆，式（3）化为），将其代入式（2）即得

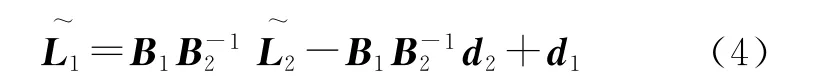
具体算法为：

（2）如果G3为空，执行第5步；否则，从G3取一种选法（不放回），组成B2和B1。

（3）如果B2可逆，执行第4步；否则，执行第2步。

（5）上述步骤完成后，得到G1，计算G1元素的成员数，记min为最少的成员数，max为最多的成员数。设q＝min。

（6）如果q＞max，算法结束；否则，取成员数为q的一个组合观测f1，将其从G1中移除，并加入G2。

（7）遍历G1，移除与f1有共同成员的组合观测。

（8）若G1为空，则算法结束；否则，执行第9步。

（9）如果成员数为q的组合观测未取完，执行第6步；如果已取完，令q＝q＋1，执行第6步。

（10）算法结束。

得到误差独立组合观测数并不能确定哪个观测值含有粗差，还需要通过其他方法作进一步探测。下面给出一种基于局部分析法的粗差探测方法。

3 基于局部分析法的粗差探测

令

由式（5）可知w的真值为零，所以式（6）计算值就是真误差。根据误差传播律可求得w的中误差σw，如果｜w｜≤2σw（偶然误差服从正态分布时），并且不考虑粗差相互抵消的情况，则可认为w定义式中的观测值都没有粗差。然后依次对其他误差独立组合观测进行分析，即可确定L～（i）的独立观测所涉及的哪些观测值不含粗差。对平差问题的其他被观测量作上述分析，同样可以确定一部分不含粗差的观测值。分析完所有的被观测量后，可确定出不含粗差的观测值，余下的即为含粗差观测值。

4 算 例

算例采用文献［9］的例7－4，是一个测角网坐标平差，如图2所示。

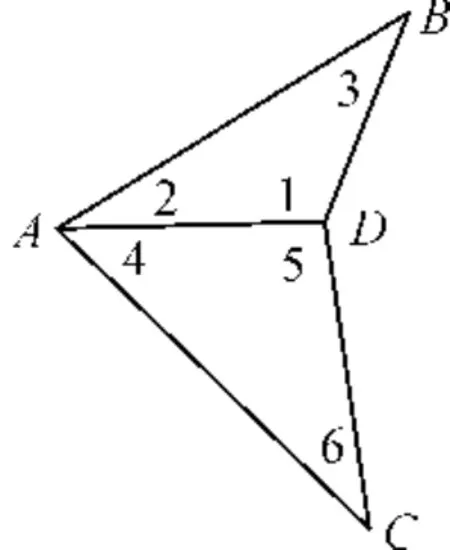
图2 测角网Fig.2 Goniometric network

图2中，A、B、C为已知点，坐标见表1，D为待定点。角度观测值为等精度（中误差1.7″，先验精度），列于表2。其中∠2含有粗差。

表1 已知点坐标Tab.1 Coordinates of known points m

表2 角度观测值Tab.2 Observed value of angles ″

设D点的坐标真值为（10 122.16m，10 312.44m），计算出6个角度被观测量的真值，列于表3的第2列。列出测角网坐标平差的误差方程，根据设计矩阵计算每个被观测量的误差独立组合观测，结果列于表3。表3中，角度单位为″。w为被观测量的观测值与组合观测的差值，σw为w的中误差，m1为误差独立组合观测数，m2为包含观测值和误差独立组合观测的总独立观测数。

根据局部分析法，由表3的m2可知，如果的独立观测有1个粗差，可以定位，多于1个时则不能定位。其他5个角度被观测量与有相同的结论。

表3 测角网分析结果Tab.3 Analysis results of goniometric network ″

以表3的第4行为例，w表示∠1与4.23∠4＋1.89∠5－912 817.3的差值，可以看出｜w｜≤2σw，于是w表达式中涉及的∠1、∠4和∠5不含粗差，分析所有被观测量可确定∠1、∠3、∠4、∠5和∠6不含粗差。那么，余下的∠2即为含粗差观测值，这与给定的观测值含粗差情况相符。

5 结 论

局部分析法逐个分析平差问题的观测值能否容忍粗差，克服了从整体上分析可容忍粗差个数的不合理性，实质上是将多维平差问题转换为多个一维问题进行讨论，其优点在于无需进行平差计算，仅依据平差问题的函数模型，因而适用于一般的平差问题。

由于各种粗差处理方法均不能正确处理不可发现和无法定位的粗差，为消除或减弱其对平差结果的影响，使用稳健估计等方法之前应当采用局部分析法分析平差问题。

［1］ BAARDA W.A Testing Procedure for Use in Geodetic Networks［M］.Delft：Netherlands Geodetic Commission，1968：5－97.

［2］ LI Deren.Gross Error Location by Means of the Iteration Method with Variable Weights［J］.Geomatics and Information Science of Wuhan University，1984，9（1）：46－68.（李德仁.利用选择权迭代法进行粗差定位［J］.武汉大学学报：信息科学版，1984，9（1）：46－68.）

［3］ ZHOU Jiangwen.Classical Theory of Errors and Robust Estimation［J］.Acta Geodaetica et Cartographica Sinica，1989，18（2）：115－120.（周江文.经典误差理论与抗差估计［J］.测绘学报，1989，18（2）：115－120.）

［4］ ZHOU Jiangwen，YANG Yuanxi.Robust Collocation［C］∥Proceedings on Robust Estimation.Beijing：Surveying and Mapping Press，1992：41－50.（周江文，杨元喜.抗差拟合推估［C］∥抗差估计论文集.北京：测绘出版社，1992：41－50.）

［5］ YANG Yuanxi.Robust Estimation for Correlated Observations［C］∥Proceedings on Robust Estimation.Beijing：Surveying and Mapping Press，1992：14－22.（杨元喜.相关观测抗差估计［C］∥抗差估计论文集.北京：测绘出版社，1992：14－22.）

［6］ YU Zongchou，LI Mingfeng.Simultaneous Location and Evaluation of Multidimensional Gross Errors［J］.Geomatics and Information Science of Wuhan University，1996，21（4）：323－329.（於宗俦，李明峰.多维粗差的同时定位与定值［J］.武汉大学学报：信息科学版，1996，21（4）：323－329.）

［7］ OU Jikun.Quasi－accurate Detection of Gross Errors（QUAD）［J］.Acta Geodaetica et Cartographica Sinica，1999，28（1）：15－20.（欧吉坤.粗差的拟准检定法（QUAD法）［J］.测绘学报，1999，28（1）：15－20.）

［8］ ZHOU Jiangwen，YANG Yuanxi.On Residuals and Leverage Observations［C］∥Proceedings on Robust Estimation.Beijing：Surveying and Mapping Press，1992：33－40.（周江文，杨元喜.论余差及杠杆观测［C］∥抗差估计论文集.北京：测绘出版社，1992：33－40.）

［9］ School of Geodesy and Geomatics Wuhan University.Error Theory and Foundation of Surveying Adjustment［M］.Wuhan：Wuhan University Press，2003.（武汉大学测绘学院测量平差学科组.误差理论与测量平差基础［M］.武汉：武汉大学出版社，2003.）