一种基于惯导信息的多普勒波束锐化图像拼接算法

胡瑞贤 王 彤 保 铮 刘保昌

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

一种基于惯导信息的多普勒波束锐化图像拼接算法

胡瑞贤*王 彤 保 铮 刘保昌

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

通过多普勒波束锐化(Doppler Beam Sharpening, DBS)图像拼接可得到大范围的地面场景图像。然而实际中雷达平台的非理想运动(载机速度矢量和姿态的变化)会造成DBS图像拼接困难。为解决此问题，该文提出了一种有效的DBS图像拼接方法。首先利用惯导信息估计载机瞬时位置和雷达波束指向，然后将它们转化到初始时刻定义的参考坐标系下，得到图像校正参数。最后利用这些参数，完成图像拼接。实测数据的处理结果表明该文方法不仅较好地补偿了载机运动误差，而且与传统方法相比可以更好地改善DBS数据的拼接性能。

图像拼接；惯导；多普勒波束锐化(DBS)

1 引言

合成孔径雷达(Synthetic Aperture Radar, SAR)通过对地面散射体进行长时间观测获得较高分辨率。由于观测场景幅宽有限，不具备快速再访能力，这种体制很难对远距离、大范围内的敌方目标进行监视跟踪。与之相比，扫描地面运动目标识别[1−3](SCAN-GMTI)采用方位扫描的工作方式，实现对大场景的快速覆盖以获取更多地面场景信息。当然这种方式需要雷达具有大的功率孔径积，而且不可能获得高的分辨率。尽管如此，由于其重访率高，可以对广域场景(如200 km×200 km)进行反复探测的优点，还是成为了战场监视最重要的方式。例如，美国的JSTARS[4]、英国的ASTOR及欧洲五国联合研制的SOSTAR都采用这种方式，旨在提供实时的广域监视和远程目标攻击指示能力。德国FGAN于2003年和2006年利用PAMIR系统进行了交通监控等实验也验证了SCAN-GMTI的性能。未来，随着天线和能源技术的发展，SCAN-GMTI模式将可能被应用到天基雷达系统中。

事实上，利用SCAN-GMTI模式进行广域监视同时可以使用 DBS技术获得大范围的地面场景图像，其测绘宽度是传统 SAR模式难以企及的。DBS[5−7]是一种粗分辨率成像技术，它利用平台运动导致的Doppler扩散来区分不同方向的回波实现比真实波束更精细的方位分辨。其前提是雷达对每一个扫描波位发射一串相干脉冲，主要处理工具是对脉冲进行处理的Doppler滤波器组。

对于每一个波位，雷达可以获得一幅DBS的扇形图像。将每个波位的图像拼接起来，就可以获得广域图像。因此，图像拼接是实现大场景测绘的重要步骤，拼接效果好坏会直接影响地面场景观测和后续的 GMTI性能。文献[8]介绍了频谱分析算法(SPECtral ANalysis, SPECAN)，并分别讨论了频率间断、方位调频率误差和多普勒中心频率误差等因素对图像拼接的影响。文献[9]提出了一种DBS子图像拼接算法，该方法在脉冲重复频率(Pulse Repetition Frequency, PRF)和脉冲积累个数M保持恒定的前提条件下，采用快速Fourier变换(FFT)对具有不同分辨率的多普勒分析的结果进行抽取，使得分辨率和数据率均保持一致，以改善图像拼接性能。文献[10,11]介绍了DBS多普勒中心估计算法，通过提高多普勒中心估计准确度来改善图像拼接性能。需要指出，这些图像拼接方法都假设载机的飞行为理想的匀速直线运动。实际上，受气流和操控等因素影响载机平台必然存在着运动误差，使得不同波位的相同距离多普勒单元无法精确配准，影响图像拼接质量。

通过惯性导航系统(Interial Navigation System,INS)和全球定位系统(Global Position System,GPS)[12,13]测量并补偿运动误差是一种可行的手段。为较好地实现DBS图像拼接，本文深入分析DBS图像拼接误差的产生原因，采用线性空间的概念对误差成因及其带来的影响进行解释，并在此基础上提出一种基于惯导数据的图像拼接算法。该方法最大的特点是同时考虑了载机瞬时位置和瞬时速度矢量的变化，利用惯导信息估计载机瞬时位置和雷达波束指向误差引起的多普勒偏移，综合两方面因素得到图像的校正参数。由于同时兼顾了姿态与位置的变化，可以显著改善图像的拼接性能；另外，采用递推方法明显降低了具体算法的运算量。需要强调的是，以往国内外研究 DBS图像拼接的文献很少，即使有讨论拼接问题的，如文献[8-11]由于波位数往往较少(一般只有几十个波位)，载机运动误差造成的拼接困难较小，在拼接过程没有考虑“误差”。而当波位较多(一般几百甚至上千个波位)时，载机误差造成的影响不能忽略，本文方法可以较好地估计并补偿载机运动误差，实现多个波位的DBS图像拼接。总之，不论从理论还是工程实现角度，本文方法都具有重要的应用价值。

2 DBS成像原理

DBS利用雷达平台运动导致的Doppler扩散来分辨不同方向的回波，以获得比真实波束更精细的方位分辨能力。如图1所示，假设载机以恒定高度H平行于地面匀速飞行，其飞行方向为X轴，垂直于X方向的平面在水平地面的交线为Y轴，竖直方向定义为Z轴。雷达天线沿正侧面放置，由于载机运动，波束指向不同场景中的杂波多普勒频率是不同的，其计算公式如下：

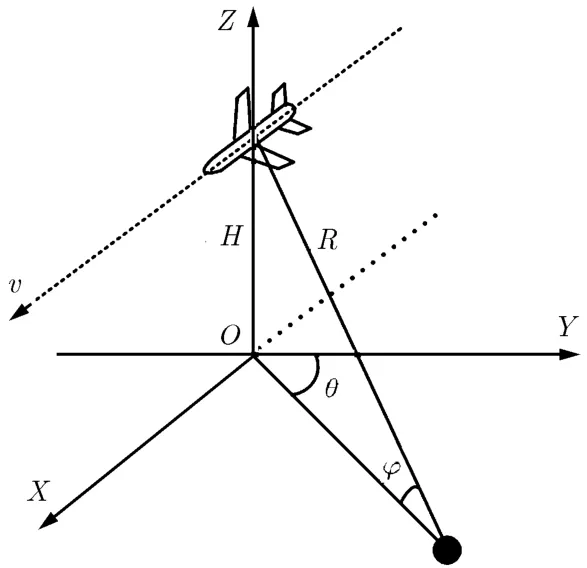
图1 机载雷达与地面散射体的关系

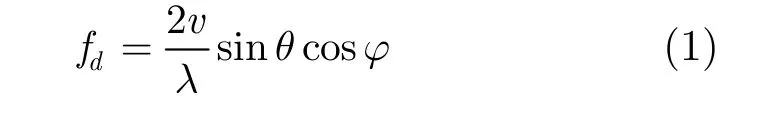
通过改变雷达波束指向对地面不同场景进行观测可获得大场景的DBS图像。相控阵雷达的工作过程比较灵活和自由，雷达操纵员通过显示控制台可以任意确定雷达的搜索空域、波束指向和工作方式。其基本工作过程如下[15]，信号产生器产生指定的低功率信号，该信号经固态放大链初步放大后，再经馈线网络分配到每个T/R组件的输入端；T/R组件对信号进行移相并进一步放大后，由天线系统向波束控制分系统指定的方向进行辐射；同时，天线把来自该方向的回波信号送到T/R组件进行放大后，送到接收分系统。图2中，每个扫描角波束的驻留位置称为一个波位，本质上表示的是雷达波束对空间的离散采样。

3 DBS图像拼接原理

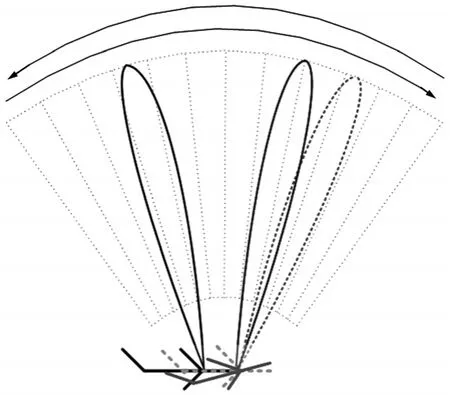
图2 雷达天线扫描示意图

上面的分析中假设载机匀速直线飞行，实际上载机的运动状况不可能是理想的，机载SAR，特别是中、低空飞行的机载SAR，由于气流不稳定的影响，运动的不稳定性较大，如果不采取运动补偿，则雷达录取的数据会有一定程度的失真，导致成像质量下降。载机受气流影响产生颠簸主要表现在两个方面[16]：一方面是载机的位置；另一方面是载机的姿态(包括偏航、俯仰和横滚等)。位置误差主要影响天线相位中心的位置，姿态变化则会影响雷达波束指向。图3给出了运动误差对图像拼接的影响。假设某一时刻，理论上雷达天线的波束指向如图 3中虚线所示，由于载机的位置和姿态发生变化，该时刻波束实际指向为图3中粗黑色波束所指的区域(类似模型亦可见图2)。此时，不仅载机的实际位置偏离理想航线，姿态误差也导致其波束照射区域与理想情况存在差异。若直接根据公式(2)将多个波位扫描结果拼接起来必然会带来严重误差，必须要借助惯性导航系统(以下简称惯导)和GPS等测得的载机实际运动情况对雷达回波数据进行补偿。

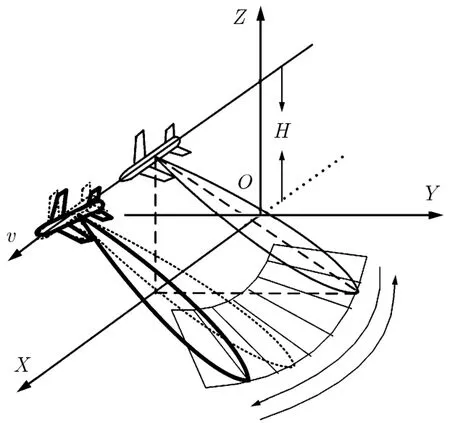
图3飞行路线扭曲时雷达波束指向示意图

惯导[12,13]可以提供运动载体的位置、速度、航向和姿态角等信息。它具有数据更新率高、短期精度高和稳定性好的优点。不足之处在于，当单独使用时定位误差随时间积累，实际使用中有必要就惯导误差的影响进行分析，本文实验部分进行了讨论。

根据上面的讨论，本文分两步补偿运动误差，第1步计算任一时刻载机的瞬时位置，第2步计算该时刻雷达波束照射范围内各地面散射体相对于初始时刻的对应坐标。

3.1 计算载机的瞬时位置

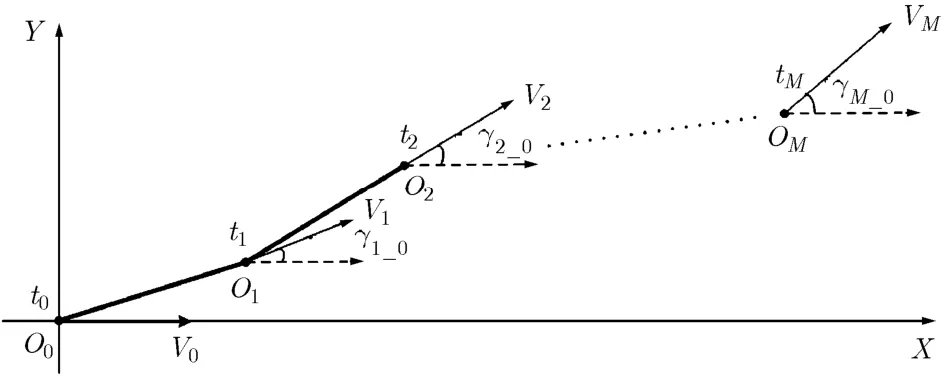
图4 载机瞬时位置的离散示意图

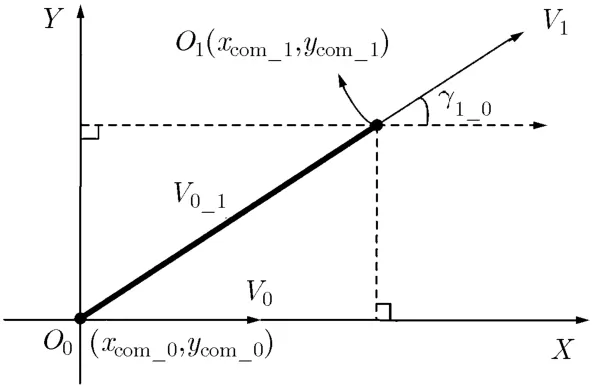
图5 O0和O1时刻载机几何关系局部图

3.2 计算目标精确坐标

上面介绍了利用偏转角γi_0估计载机瞬时位置的方法，事实上这个角度更重要的作用是对波束指向进行校正以获得地面散射体的真实坐标。为讨论简单，将图3的模型向z=0平面投影得到图6。初始t0时刻，载机从O点沿X轴方向飞行，阵面法线指向为Y方向；ti时刻载机实际位置为Oi，受气流影响航线偏离X轴，其实际飞行方向Xi轴与初始时刻X轴之间的夹角也为γi_0，相应的阵面法线指向为Yi。补充说明，由于载机在Z方向存在颠簸，XOY平面与XiOiYi平面应该存在空间夹角，此处为简化处理，认为载机飞行高度保持恒定，即Z方向颠簸很小可以忽略，这种假设与实际惯导测量结果也是吻合的。

以上模型可以从线性空间角度来理解。将t0时刻的XOY平面记为线性空间V0，向量O0X和O0Y为该线性空间中的一组线性无关的正交基，记为和 ，则

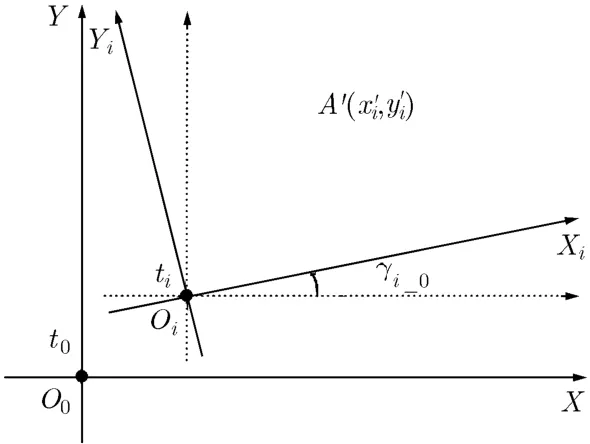
图6 运动轨迹旋转扭曲导致的坐标轴旋转

4 图像拼接算法

(5)读入第ti+1时刻数据和惯导信息，重复以上步骤，直到所有波位数据全部处理结束。

5 实测数据处理结果

下面以一组X波段SCAN-GMTI数据为例来验证本文的基于惯导补偿的 DBS图像拼接算法的性能。本节首先就惯导精度对于DBS图像拼接的影响进行分析，接着分别给出传统方法和本文方法的DBS图像拼接结果并进行比较。雷达系统工作在X波段，信号带宽约为20 MHz，方位向3个接收天线，相邻天线间距为0.4 m，载机速度约为120 m/s，场景中心距离 50 km，脉冲个数 128，波束扫描范围-30°～+30°，俯仰角 4°。

上面的分析中并未考虑惯导误差的影响，换言之采用本文方法对实测数据进行处理时假设载机惯导参数是精确的，这在实际情况中几乎是不可能的。由于惯导是一个时间积分系统，其重要组成部件陀螺仪和加速度计(它们分别用来检测运动载体在惯性空间中的角运动和线运动)存在误差将导致惯导的导航误差随时间积累。因此在介绍本文的DBS图像拼接结果之前有必要就惯导精度对 DBS图像拼接的影响进行分析说明。本节首先用实测惯导数据进行仿真试验验证惯导精度对图像拼接的影响，然后用本文方法处理实测数据以验证该方法的性能。

通常，随机漂移率为0.015°/h(相当于地球自转角速率的 0.1%)的陀螺仪，精度可以满足一般惯导要求(位置误差1 n mile/h)。实践中，常用0.01°/h来表征惯性级陀螺仪的最低精度。对式(8)进行推导，得到由惯导误差引起的图像拼接误差的计算公式

图7表示惯导误差对运动补偿的影响。其中，*表示不考虑惯导误差时某地面散射点的位置(作为相对参考点)，·表示惯导存在精度误差和随机漂移时的该散射点的随机分布(图 7(a)-图 7(c)均仿真了1000点)。在仿真时，假设惯导精度误差服从高斯分布。另外，由于载机飞行时间较短，认为随机漂移率随时间线性变化。图 7(a)表示惯导精度为 10−5，随机漂移率为0.01°/h，图7(d)为图7(a)右上角点迹的局部放大图(另外 3个方向的点迹与此类似)，图7(b)惯导精度为 10−5，随机漂移率为 0.015°/h，图7(e)为图7(b)右上角点迹的局部放大图(另外3个方向的点迹与此类似)，图7(c)表示惯导精度为 10−3，随机漂移率为0.015°/h的散射点随机分布。由于惯导随机漂移方向未知，图中的随机点列均形成4条点迹。理论上讲，这与实际情况不吻合，但这些点迹近似呈对称分布，并不影响我们的分析结果。在图 7(a)-图7(c)中以*为圆心，距离分辨率为半径做圆，圆内部的点均位于一个分辨单元内，表明存在惯导误差时，目标坐标的计算结果依然是准确的，即此时惯导精度对图像拼接影响可以忽略。但是由图 7(c)可以看出部分随机实验结果出现在了圆外，表明此时惯导精度对系统的影响是需要考虑的，即目标坐标的结果是存在误差的。由于本文所采用的惯导实测数据的精度为 10−5，随机漂移率为0.015°/h，与图7(c)的情况吻合，因此采用本文方法进行图像拼接时可以忽略惯导误差对图像拼接的影响。

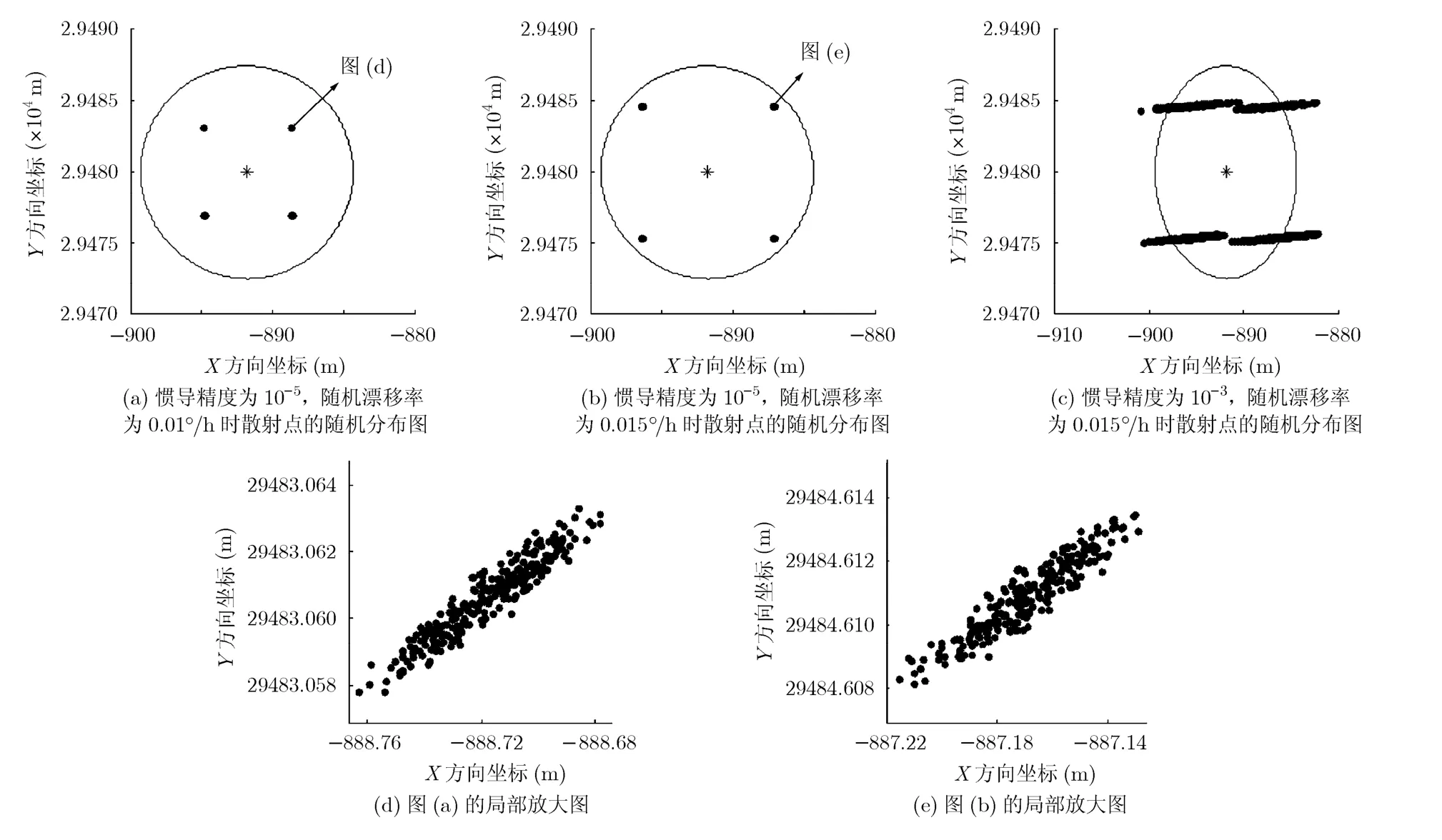
图7 惯导误差对分辨率的影响

为了与本文方法进行比较，首先给出一种未进行运动补偿采用SPECAN方法得到的DBS图像拼接结果，如图8(a)所示。直观上讲，这幅DBS场景图像主要存在以下问题：图像中一些特显点如桥梁、公路等由于拼接误差在水平方向存在偏移不能重合，最多偏移十几个单元，由此导致图像出现严重的模糊和重影等问题，这样的处理结果显然很不理想，且不利于后续的目标定位精度要求。原因在于，这种传统方法在补偿运动误差时，只是从整体上沿某个方向补偿了一个平移量，忽略了载机运动的非理想性；其次从另一个角度，根据系统参数，即使按照每秒100 m的速度来估计，扫描1 min内载机的移动距离也有将近6千米，原始的假设已经明显不适用了，必须要采用更加精确的补偿算法。

图8(b)是采用本文方法对数据进行运动补偿后，将多次扫描数据拼接起来获得的处理结果。与图8(a)相比，图中一些典型的地形地貌特征和重要场景(如沟壑、桥梁、高速公路等)比较明显；这样的场景性能显然有利于后续的运动目标定位。总之，实际处理结果与理论分析非常吻合，表明本文方法对于改善多次扫描的DBS图像结果具有广泛的适应性及重要的实用价值。

6 结论

针对多次扫描的 DBS图像拼接时存在的重影等现象，本文在深入分析问题成因的基础上提出了一种基于惯导数据的DBS图像拼接方法，充分利用惯导提供的信息，补偿载机位置和姿态变化对实测数据的影响，取得了明显效果；另外由于实现方法简单，在并未明显增加运算量的前提下，多个波位DBS图像的拼接结果得到明显改进。

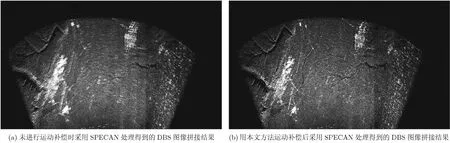
图8 DBS图像拼接结果

[1] Guttrich G L and Sievers W E. Wide area surveillance concepts based on geosynchronous illumination and bistatic UAV or satellite reception[C]. IEEE Aerospace Conference Proceedings, Aspen, CO, 1997: 171-180.

[2] Cerutti-Maori D, Klare J, Brenner A R,et al.. Wide-area traffic monitoring with the SAR/GMTI system PAMIR[J].IEEE Transactions on Geoscience and Remote Sensing, 2008,46(10): 3019-3030.

[3] Zou Bo, Zhen Dong, and Liang Dian-nong. Research on Scan-GMTI technology of airborne MIMO radar based on STAP[C]. ICSP 2010 Processding, Beijing, Oct. 24-28, 2012,1973-1976.

[4] Entzminger J N, Fowler C A, and Kenneally W J.JointSTARS and GMTI: past, present and future[J].IEEE Transactions on Aerospace and Electronic Systems, 1999,35(2): 748-761.

[5] 赵宏钟, 谢华英, 周建雄, 等. 匀加速运动平台下的大斜视DBS成像方法[J]. 电子学报, 2010, 38(6): 1280-1286.

Zhao Hong-zhong, Xie Hua-ying, Zhou Jian-xiong,et al..High squint DBS imaging based on constant acceleration movement platform[J].Acta Electroinca Sinca,2010, 38(6):1280-1286.

[6] 刘凡, 赵凤军, 邓云凯, 等. 一种基于最小二乘直线拟合的高分辨率 DBS成像算法[J]. 电子与信息学报, 2011, 33(4):787-791.

Liu Fan, Zhao Feng-jun, Deng Yun-kai,et al.. A new high resolution DBS imaging algorithm based on least squares linear fitting[J].Journal of Electroincs&Information Technology, 2011, 33(4): 787-791.

[7] Long Teng, Lu Zheng, Ding Zegang,et al.. A DBS Doppler centroid estimation algorithm based on entropy minimization[J].IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3703-3712.

[8] Cumming I G and Wong F H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M].Norwood, MA, Artech House, 2004: 369-399.

[9] 刘寅. 扫描方式下DBS子图像拼接算法[J]. 雷达科学与技术,2005, (2): 91-95.

Liu Yin. Combination algorithm for DBS sub-image in scanning mode[J].Radar Science and Technology, 2005, (2):91-95.

[10] 左磊, 李明, 张晓伟. DBS多普勒中心无模糊估计新方法[J].西安电子科技大学学报, 2011, 38(5): 196-203.

Zuo Lei, Li Ming, and Zhang Xiao-wei. Doppler centroid estimation without ambiguity in DBS[J].Journal of Xidian University, 2011, 38(5): 196-203.

[11] 万红进, 李辉. DBS多普勒质心估计算法研究[J]. 火控雷达技术, 2010, 39(2): 37-40.

Wan Hong-jin and Li Hui. Study on DBS Doppler centroid estimation algorithm[J].Fire Control Radar Technology, 2010,39(2): 37-40.

[12] Farrell J and Barth M. The Global Positioning System and Inertial Navigation[M]. NY, McGraw Hill, 1999: 217-273.

[13] 李跃. 导航与定位-信息化战争的北斗星[M]. 北京: 国防工业出版社, 2008: 384-446.

Li Yue. Navigation and Positioning-the Big Dipper in Information War[M]. Beijing: National Defense Industry Press, 2008: 384-446.

[14] 吴顺君, 梅晓春. 雷达信号处理和数据处理技术[M]. 北京:电子工业出版社, 2008: 135-139.

Wu Shun-jun and Mei Xiao-chun. Radar Signal Processing and Data Processing Technology[M]. Beijing: Press of Electronic Industry, 2008: 135-139.

[15] 贲德, 韦传安, 林幼权. 机载雷达技术[M]. 北京: 电子工业出版社, 2006: 170-200.

Ben D, Wei C A, and Lin Y Q. Airborne Radar Technology[M]. Beijing: Press of Electronic Industry, 2006: 170-200.

[16] 保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京:电子工业出版社, 2005: 185-195.

Bao Z, Xing M D, and Wang T. Radar Imaging Technology[M]. Beijing: Press of Electronic Industry, 2005:185-195.

A Novel Algorithm for Stitching Doppler Beam Sharpening Images Based on INS Information

Hu Rui-xian Wang Tong Bao Zheng Liu Bao-chang
(Key Lab. of Radar Signal Processing,Xidian University,Xi’an710071,China)

By stitching Doppler Beam Sharpening (DBS) images together, a wide swath ground image is obtained.In practice, however, there are some difficulties in stitching due to the nonideal movement (variation of the velocity vector and the attitude) of the radar platform. To deal with these problems, a novel method is proposed, which can stitch the DBS images effectively. The Interial Navigation System (INS) information is employed to estimate the instantaneous position of the aircraft and the radar beam direction, both of which are then transformed to the original reference coordinate so that the corrected parameters of the image can be obtained. Finally, by using these parameters, the image stitiching is achieved. Processing results of measured data show that the proposed method not only compensates the motion error excellently, but also significantly outperforms the traditional algorithm in stitching performance.

Image stitching; Interial Navigation System (INS); Doppler Beam Sharpening (DBS)

TN957.52

A文章编号：1009-5896(2012)06-1337-07

10.3724/SP.J.1146.2011.01019

2011-09-29收到，2011-12-29改回

国家自然科学基金(60872140)资助课题

*通信作者：胡瑞贤 hu12rui3@yahoo.com.cn

book=6,ebook=272

胡瑞贤： 男，1984年生，博士生，研究方向为 SAR-GMTI、广域GMTI和空时自适应信号处理.

王 彤： 男，1974年生，教授，博士生导师，现从事信号与信息处理的研究工作，特别是针对雷达探测方向的阵列信号处理、包括空时二维自适应处理、雷达成像和地面动目标检测等.

保 铮： 男，1927年生，教授，博士生导师，中国科学院院士，从事雷达系统和信号处理的教学和研究工作，研究面涉及自适应信号处理、阵列信号处理、非线性信号处理、雷达成像和目标识别等雷达信号处理的重要领域.

刘保昌： 男，1981年生，讲师，研究方向为 SAR-GMTI、广域GMTI和双基SAR成像.