一种改进的基于波前重构的圆周SAR三维成像算法
王本君 闵 锐 皮亦鸣
(电子科技大学电子工程学院 成都 611731)
一种改进的基于波前重构的圆周SAR三维成像算法
王本君 闵 锐*皮亦鸣
(电子科技大学电子工程学院 成都 611731)
与传统的直线SAR相比,圆周SAR(CSAR)具有对场景进行3维成像的能力。该文提出了一种基于波前重构的圆周SAR 3维成像的新方法,该算法通过补偿掉雷达运动轨迹引入的相位项的方法实现了图像的聚焦,避免了Hankel函数的计算,从而大大降低了算法实现的复杂度。仿真与实测CSAR数据成像结果验证了该算法的有效性。
圆周合成孔径雷达;3维成像;波前重构
1 引言
由于具有高分辨成像能力,合成孔径雷达(SAR)在民用和军事领域得到广泛应用,然而在有些应用场合如高精度测绘、精确打击等,传统SAR系统所提供的2维成像信息已不能满足需要。与传统的直线SAR相比,圆周SAR能以较简单的模式获得目标更为全面的散射信息。圆周SAR成像由于其特殊的圆周孔径,常规的SAR成像算法,如RD, CS等已不再适用。时域相关(TDC)算法与后向投影(BP)算法可用于圆周SAR成像,且其成像机理简单,成像结果较为精确,但这两种算法计算量较大,因此可以作为其他算法的验证算法[1,2]。基于平面波近似的一类成像算法虽然可以提高运算速度,但仅适用于远场成像,在近场CSAR成像中,该类算法的成像精度较差[3]。
文献[4-6]根据波方程的基本理论,提出了适用于圆周SAR的3维成像算法。该算法首先将探测场景沿高度向分割成若干个高度层,然后利用匹配滤波技术形成一系列的2维图像,最后将得到的2维图像序列通过3维重建技术生成3维图像。该算法在匹配滤波时需要计算复杂的Hankel函数。基于该算法,本文提出了新的CSAR 3维成像算法。新算法通过补偿掉雷达运动轨迹引入的相位项的方法得到2维图像,避免了Hankel函数的计算,从而大大降低了算法实现的复杂度。
2 CSAR成像的信号模型
图1为CSAR系统的几何关系示意图。雷达在高为H的平面以半径Rgc沿圆周匀速运动,雷达在空间域中的坐标为(Rgccosθ,Rgcsinθ,H),其中θ∈[0,2π)表示慢时间方位角域。当雷达沿圆周轨迹运动时,其波束始终覆盖整个以原点为中心、半径为R0的圆形场景。为分析简便,假设所有散射点均位于地面(3.2节将对散射点分布于3维空间的情况进行分析),目标散射特性为f(x,y),则雷达接收的回波信号经快时间匹配滤波后可表示为
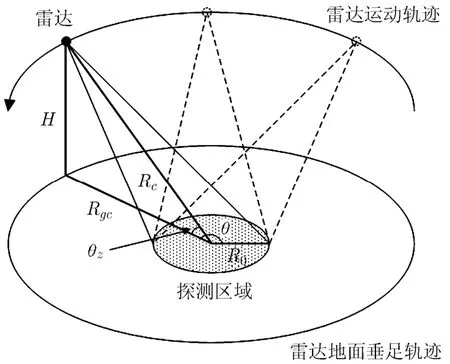
图1 CSAR系统几何关系示意图

3 CSAR波前重构3维成像算法
本文中提出的CSAR 3维成像算法首先将原始CSAR回波数据转换到地平面,以消除雷达平台高度H的影响,然后将地平面CSAR信号谱中雷达运动轨迹半径带来的相位项补偿掉,获得地平面的目标2维空间频率谱,最后将地平面的目标2维空间频率谱乘以相位函数,得到任意高度平面的目标 2维空间频率谱,对空间频率谱做2维逆傅里叶变换即可得到不同高度面的2维图像序列,从而形成3维图像。
3.1 CSAR地平面2维聚焦


3.2 3维空间中成像高度平面变换
上述 CSAR成像是基于目标位于地平面的假设,因此成像结果可看作是目标的 3维特性函数f(x,y,z)在z=0平面的 2维分布即f(x,y,0)。而实际上,我们是需要对在不同的(x,y)点有不同高度值的3维目标进行3维成像。
对于 3维目标场景,散射点高度为z(x,y),则散射点与雷达间的距离应调整为式(12):R(θ)


3.3 算法流程
通过上述分析,为了将时间空间域中的原始CSAR数据转化为空间域中的目标图像,本文提出了一种改进的基于波前重构的3维成像算法,其步骤如下:
步骤1 CSAR回波信号经快时间匹配滤波,得到快时间频率-方位角域信号s(ω,θ);
3.4 算法性能分析

4 仿真与实测数据处理
本节将通过对多个点目标的仿真和 GTRI(Georgia Tech Research Institute) 3维转台数据的处理,来验证算法的有效性。
首先,我们通过对多个点目标的仿真来验证算法的有效性。假设雷达探测的3维场景中分布多个(本文取为11个)单位散射强度的散射点,散射点分布于4个高度面,其具体位置如表1所示。雷达在50 m高度面沿圆周轨迹运动,其波束始终指向场景中心并覆盖整个场景,波束入射角为60°。雷达发射信号的载频为9.6 GHz,带宽为1.2 GHz。雷达沿方位角数据采样区间为[0,2π)。
利用本文提出的成像算法,在高度为-1.2 m,-0.4 m, 0.4 m和1.2 m的高度面生成的4幅2维图像如图2所示。从图中可以看出,散射点只有在所在高度层才能很好地聚焦,在图像中表现为亮点;而散焦的散射点在图像中表现为幅度较低的圆环(由于散焦点对应的圆环的幅度很低,为能在图像中较好地显示出来,图2中显示的图像幅度为实际图像幅度的对数)。由2维图像序列构建的3维图像如图3所示。显然利用本文中的成像算法,我们获得了较为精确的3维图像。
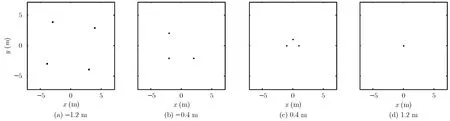
图2 不同高度层的2维图像
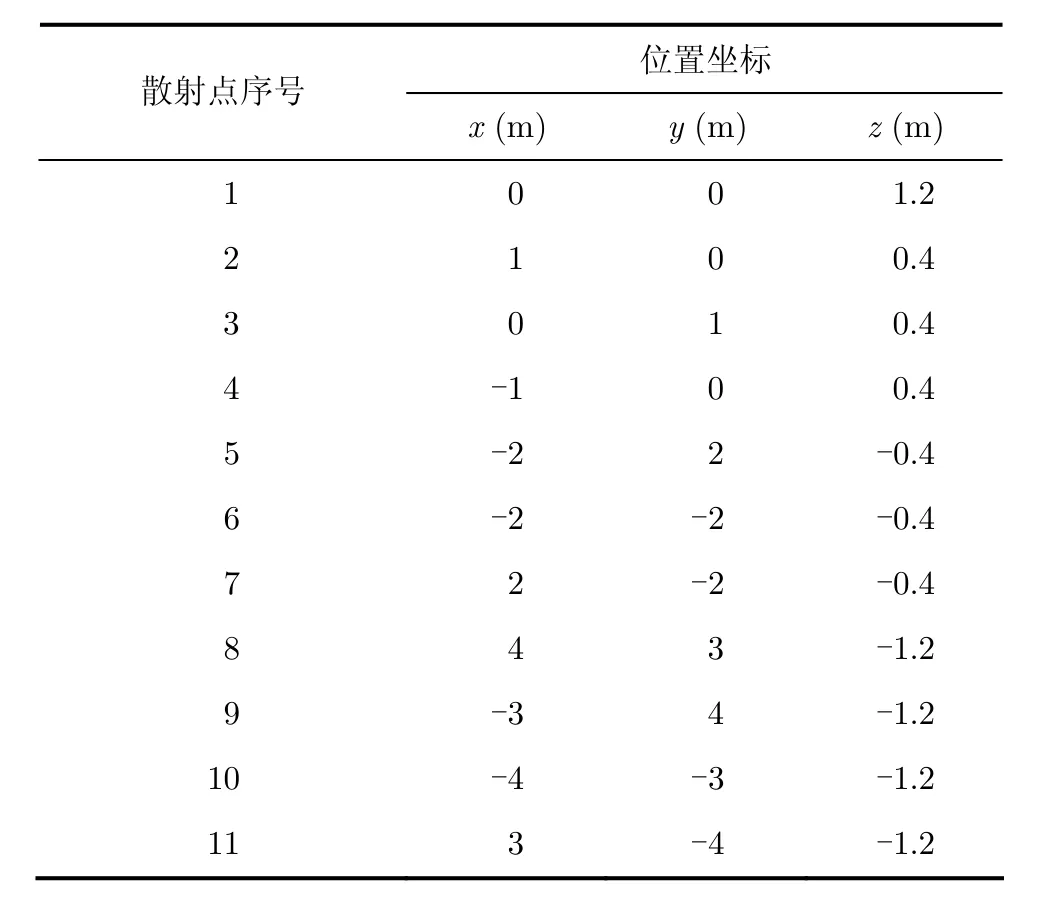
表1 3维场景中散射点的分布
为进一步验证算法的有效性,我们利用实际数据对真实场景进行成像。本文中选取的数据为GTRI 3维转台数据中的一部分[1,4],其中部分相关参数如表2所示。
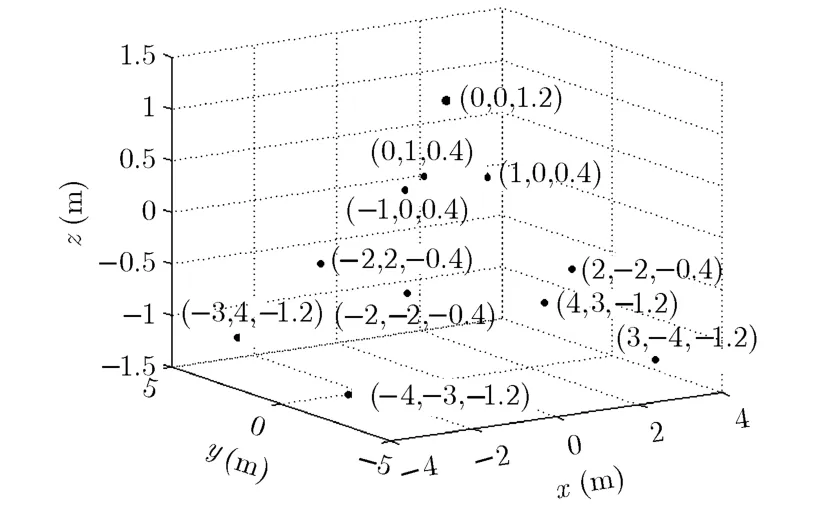
图3 3维图像
利用本文中提出的算法,我们得到场景在z=-1.25 m和0.75 m高度处的2维切片如图4所示。散射点只有在其所在高度面才能很好地聚焦,偏离其所在高度越大,散焦越严重。图4中z= 0.75 m高度面(图 4(a))中的两个角反射器聚焦程度相对较好,而炮管在z=0.75 m高度面(图4(b))聚焦程度相对较好。
5 结论
本文提出了一种改进的基于波前重构的适用于圆周SAR系统的3维成像新算法。该算法在生成图像的过程中,通过补偿掉雷达运动轨迹的影响进行聚焦,避免了Hankel函数的计算,从而降低了算法实现的复杂度;同时该算法避免了平面波近似,保证了成像结果的准确性。仿真与实际数据成像结果表明该算法是一种适用于圆周 SAR系统的有效新算法。

图4 -1.25 m, 0.75 m高度面的2维图像

表2 GTRI 3维转台数据相关参数
[1] Bryant M L, Gostin L L, and Soumekh M. 3-D E-CSAR imaging of a T-72 tank and synthesis of its SAR reconstructions[J].IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(1): 211-227.
[2] Sharma R. Analysis of circular aperture SAR image formation[C]. Signals, Systems and Computers, Conference Record of the Forty-Third Asilomar Conference, Pacific Grove, CA, Nov. 1-4, 2009: 482-487.
[3] 林赟, 谭维贤, 洪文, 等. 圆迹 SAR 极坐标格式算法研究[J].电子与信息学报, 2010, 32(12): 2802-2807.
Lin Yun, Tan Wei-xian, Hong Wen,et al.. Polar format algorithm for circular synthetic aperture radar[J].Journal of Electronics&Information Technology, 2010, 32(12):2802-2807.
[4] Soumekh M. Synthetic Aperture Radar Signal Processing with MATLAB Algorithm[M]. New York: Wiley, 1999:491-521.
[5] Soumekh M. Reconnaissance with slant plane circular SAR imaging[J].IEEE Transactions on Image Processing, 1996,5(8): 1252-1265.
[6] Burki J and Barnes C F. Slant plane CSAR processing using Householder transform[J].IEEE Transactions on Image Processing, 2008, 17(10): 1900-1907.
[7] Flores-Tapia D, Thomas G, Ashtari A,et al.. 3D breast microwave imaging based on wavefront reconstruction[C].Proceedings of the 28th IEEE EMBS Annual International Conference, New York, Aug. 30–Sept. 3, 2006: 2542-2545.
[8] Flores-Tapia D, Thomas G, and Pistorius S. A wavefront reconstruction method for 3-D cylindrical subsurface radar imaging[J].IEEE Transactions on Image Processing, 2008,17(10): 1908-1925.
[9] Flores-Tapia D, Thomas G, and Pistorius S. Wavefront reconstruction of 3D cylindrical subsurface radar imagery: a study on synthetic phantoms[C]. Radar Conference, Rome,May 26-30, 2008: 1-6.
[10] Flores-Tapia D, Thomas G, and Pistorius S. Wavefront reconstruction method for subsurface radar imagery acquired along circular and planar scan trajectories[J].IEEE Transactions on Aerospace and Electronic Systems, 2010,46(3): 1346-1363.
[11] Flores-Tapia D and Pistorius S. Spatial sampling constraints on breast microwave radar scan acquired along circular scan geometries[C]. Biomedical Imaging: From Nano to Macro,Chicago, IL, March 30–April 2, 2011: 496-499.
An Improved Wavefront Reconstruction Method for Circular SAR 3D Imaging
Wang Ben-jun Min Rui Pi Yi-ming
(School of Electronic Engineering,University of Electronic Science and Technology of China,Chengdu611731,China)
The Circular Synthetic Aperture Radar (CSAR), unlike the linear SAR, has the capability to extract three-dimensional imaging information of a target scene. In this paper, a novel CSAR wavefront reconstruction method is proposed for three-dimensional imaging. The proposed method compensates the effects of the phase components introduced by the radar’s trajectory to form reconstructed image, which avoids calculating the complicated Hankel function. Thus the complexity of the algorithm can be reduced. Finally, the validity of the presented method is clarified by both simulated data and experimental data sets.
Circular Synthetic Aperture Radar (CSAR); Three-dimensional imaging; Wavefront reconstruction
TN957.52
A文章编号:1009-5896(2012)06-1351-05
10.3724/SP.J.1146.2011.00954
2011-09-16收到,2012-02-24改回
中央高校基金(ZYGX2009Z005)和电子科技大学青年基金(JX0803)资助课题
*通信作者:闵锐 minrui@uestc.edu.cn
王本君: 男,1987年生,硕士生,研究方向为雷达信号处理、SAR 3维成像.
闵 锐: 男,1978年生,讲师,研究方向为图像传输、雷达成像与信号处理.
皮亦鸣: 男,1968年生,教授,博士生导师,研究方向为雷达信号处理、定位与导航、图像高速处理与传输等.

