基于细粒度任务分配的空时自适应并行处理算法研究
王 超 刘 伟 袁培苑
(北京理工大学信息与电子学院 北京 100081)
基于细粒度任务分配的空时自适应并行处理算法研究
王 超 刘 伟*袁培苑
(北京理工大学信息与电子学院 北京 100081)
对于空时自适应信号处理(Space-Time Adaptive Processing, STAP)算法的并行处理问题,传统方法以粗粒度的划分方式将 STAP算法分配到特定硬件系统中的不同处理器中,利用处理器间的流水计算来提高系统计算吞吐量。该文分析了传统并行处理方法的缺陷:粗粒度的任务划分方式牺牲了 STAP算法的并行度;传统处理方法仅能适用于特定的系统环境。针对上述情况,该文提出一种基于细粒度任务分配的 STAP并行处理方法,该方法分为以下3个步骤:构建细粒度的DAG(Direct Acyclic Graph)形式的STAP算法任务模型;使用统一拓扑结构模型描述不同结构的目标硬件系统;基于细粒度任务分配算法将任务模型分配到拓扑结构模型中的处理器实现并行计算。实验结果表明该并行处理方法能够达到良好的加速比,并且对于不同的STAP应用系统具有很好的适应性。
信号处理;空时自适应系统;并行处理;任务分配;细粒度
1 引言
空时自适应处理(STAP)是新一代相控阵雷达充分利用空域和时域信息通过空时2维滤波来抑制杂波与目标检测的一项关键技术,广泛应用于机载预警雷达、机载合成孔径雷达、机载战场侦察雷达及星载雷达、舰载雷达等实现杂波抑制与运动补偿[1]。STAP面对着根据外界杂波及干扰的环境实时地求解自适应权值向量的问题[2,3]。求解权值向量是一个高密集计算型问题,运算量巨大,数据交互复杂,通常采用并行处理技术提高算法的实时性。
传统的并行处理方法将STAP算法流程划分为若干粗粒度的计算任务,分配计算任务到专用的硬件环境中的处理器,利用处理器间的流水计算来提高系统计算吞吐量[4−6]。文献[7]提出了一种通用的STAP并行计算模型,并给出了适用于流水计算的粗粒度任务分配方法。粗粒度任务划分易于实现,但是牺牲了算法的并行度[8]。国外对于细粒度STAP并行处理也有一些研究。文献[9]引入遗传算法解决STAP并行化处理过程中的细粒度任务分配问题,但是该方法仅能适用于具有全交换拓扑结构的硬件环境中。文献[10]提出了一种细粒度数据划分方法,并在GPU(Graphics Processing Unit)中实现了单指令多数据流形式的STAP并行处理,但是GPU并不能应用于机载平台等嵌入式环境,这就限制了该方法实际应用性。
其次,传统的处理方法往往只适用于特定的STAP应用系统[4−6,9]。特定应用系统中限定了系统参数,包括STAP处理通道数、脉冲数及处理距离单元数等信息;还限定了硬件环境信息,包括处理器的数量与处理器间的互联方式。当系统参数变化或硬件环境改变时,传统方法往往不再适用,这大大限制了传统方法的通用性。因此研究一种具有高并行度并且具有拓扑结构独立性的并行处理方法对于STAP算法的应用是非常有意义的。
我们可以分以下3个步骤实现STAP的并行处理:(1)划分STAP算法为细粒度的计算任务,建立细粒度的任务模型。相比于粗粒度的方式,细粒度的划分后任务模型具有更高的并行度[10]。(2)建立统一的拓扑结构模型,在模型参数中定义处理器的数量以及互联方式等信息,对于不同的目标硬件环境,配置不同的模型参数。(3)基于任务分配方法,完成任务模型到拓扑结构模型的分配。细粒度划分后计算任务的数量以及任务间的计算约束关系会变得非常复杂[10]。直接实现任务分配是非常困难的,更好的方法是选取一种合适的任务分配算法实现计算任务集到多处理器平台的映射。任务分配算法以优化加速比为目标通过计算任务间的约束关系及并行性选择将可并行的任务分配到不同的处理器实现独立计算。
2 基于细粒度任务分配的STAP处理方法
2.1 任务模型


2.2 拓扑结构模型
拓扑结构模型为目标硬件系统的抽象,包含了处理器的信息及处理器间的互联信息。定义拓扑结构模型TP = {U,CH}。其中U为有限的处理器集合,U中的每个元素表示一个独立的处理器;CH为有限的通信通道集合,CH中的每个元素都表示处理器间的通信传输通道,传输通道分为单向传输通道和双向传输通道。对于不同的硬件环境,需要配置不同的U与CH。
假设拓扑结构模型具有以下两个特性:(1)非抢占式:处理器只有在完成当前计算任务才能开始执行新的任务;(2)并发性。处理器可以同时执行并发的计算任务和通信传输任务。任务模型中的节点V需要被分配到拓扑结构模型中不同处理器U。当间的数据传输eij就转变为处理器间的 IPC(Inter Processor Communication)操作,并需要将该 IPC操作分配到连接uk与ul的传输通道中。处理器间传输通道的选择一般采用最短路径准则。
2.3 任务分配算法
任务分配算法以优化加速比为目标将任务模型中的节点v分配到拓扑结构模型的处理器u中,并根据节点的分配完成IPC操作到传输通道的分配。任务分配是一个具有 NP(Non-deterministic Polynomial) 完备性的问题,很难获得最优的分配结果,因此常见的任务分配算法一般基于启发式算法获得次优结果[11]。
在现有的分配算法中,大都在分配过程中假定了理想的硬件环境[11−14],即不限定处理器数目及互联通道数目,这并不符合于我们建立的拓扑结构模型。DLS(Dynamic Level Scheduling)是唯一具有拓扑结构独立性的分配算法[15],即DLS脱离了拓扑结构对分配算法的影响。在分配过程中,DLS实时计算分配不同节点到不同处理器的动态优先级 DL(Dynamic Level),并依照DL顺序完成节点分配。因此我们选择DLS完成细粒度STAP任务模型的分配。
在每个分配步骤中,DLS中以∑表示当前状态的已分配信息,分配节点vi到处理器uj时需要完成:(1)根据pr(vi)的分配信息,完成vi前向IPC操作分配;(2)完成vi到uj的分配。∑包含已分配节点以及IPC的st, end等分配信息。统计出vi执行前所需要完成的传输任务集合,如下:
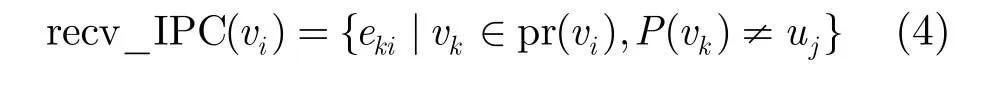
IPC操作只能够分配在拓扑结构模型中定义的通信通道,并根据各通信通道的已分配状态确定IPC操作的起始执行时间。DA表示所有recv_IPC(vi)的最后结束时间,同时也表示了∑下vi在uj上的数据就绪时间。
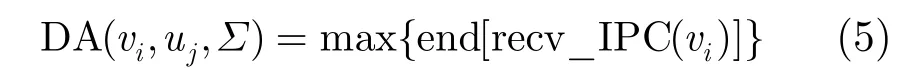
由 DA可以计算出st(vi),代入式(3)计算式end(vi)完成vi在pj上的分配。当前阶段结束后更新∑。∑的迭代更新确保每个分配阶段都可以完全获取各处理器和通信通道的任务分配信息,并依此完成新任务的分配。式(6)中TF(uj,∑)表示∑下uj的空闲时间。
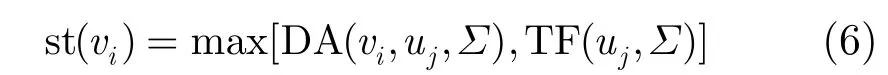

综上所述,基于细粒度任务分配的STAP并行处理方法分为3个步骤:(1)构建任务模型。根据系统参数建立STAP处理流程图,将其划分为细粒度的任务集并建立任务DAG图。DAG中每个节点的计算粒度确定后,其计算开销以及边界的传输开销可以通过实际测试获取。(2)构建拓扑结构模型。拓扑模型TP = {U,CH}参数中应明确定义处理器的个数以及处理器间的互联关系。根据目标硬件环境配置拓扑结构模型参数。(3)任务分配过程。使用DLS算法实现任务模型到拓扑结构模型的映射。可由式(7)估算分配结果的加速比。最终输出并行分配结果;并行分配结果中包括:计算任务到处理器的映射关系、IPC任务到传输通道的映射关系以及计算任务和IPC的执行顺序关系。
3 并行处理的实现
基于细粒度任务分配的并行处理方法分3步完成,其中任务分配过程使用较为成熟的DLS分配算法,因此实现STAP应用系统的并行处理时需要完成细粒度任务模型的构建以及拓扑结构模型的配置。
3.1 细粒度任务模型构建
全自适应STAP算法计算量过于庞大,工程应用一般选择基于频域降维的 3DT-SAP算法。本节以3DT-SAP算法为例简述细粒度STAP任务模型的构建方法。设置脉冲数为M,阵元数为N,距离单元数为L,参照文献[4,5]中的 STAP处理流程构建粗粒度的任务DAG图,如图1(a)所示。图中的节点表示计算任务,节点间的连接箭头表示计算任务间的数据传输。
由数据分配节点将数据分发到N个多普勒滤波节点,每个节点完成L次M点FFT,完成后数据由STAP数据分配节点分配到M−2个数据组合节点中。对于每个数据组合节点,将N个处理通道中相邻的3组脉冲数据组合在一起[15]。组合后的数据由权值生成节点计算得到自适应权值。权值生成可以通过如下步骤完成:组合数据转置后经由QR分解节点得到3N×3N维的上三角矩阵A;联合空时 2维导向矢量s求解两次线性方程组计算得到自适应权值矢量w,如图1(b)所示。最终由自适应权值联合数据组合节点的输出完成滤波过程,得到 STAP的输出。
传统的 STAP并行处理方法通常使用粗粒度QR分解操作,牺牲了算法的并行度,本文将采用一种细粒度的QR分解方法。计算权值的距离门数Lls应满足自适应权值的收敛条件,取Lls=3 ×3N构成9N×3N的数据矩阵来求解权值向量[4]。将输入Lls×3N阶矩阵依照行顺序分为K块(Lls/K)×3N阶子矩阵,在实际应用中一般保证3N为Lls/K的整数倍;将QR分解分割为两种细粒度的计算任务:消除下三角元素操作以及消除上三角元素操作。
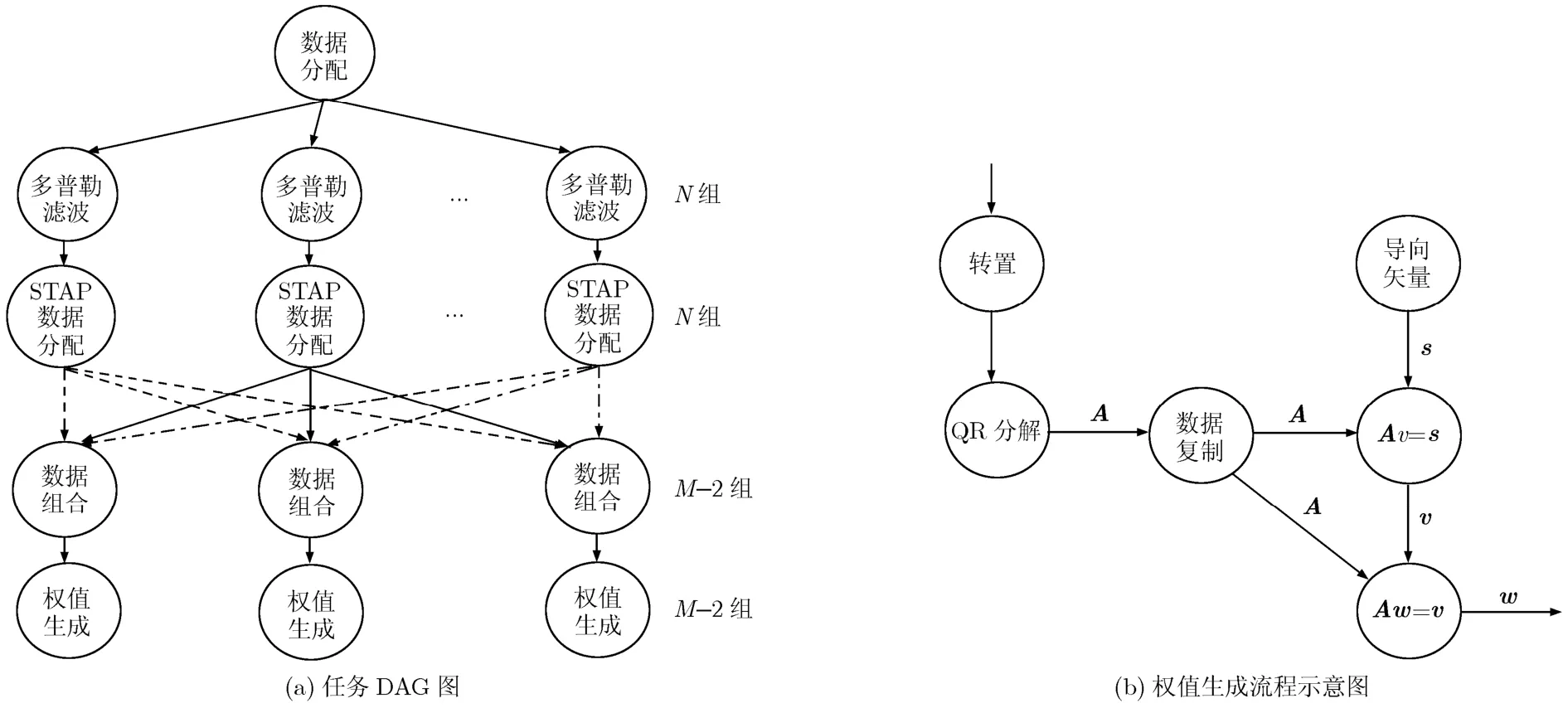
图1 粗粒度任务模型DAG
(1)消除下三角操作过程:假设子矩阵M1的前r列元素全部为0,r+1列元素非 0,使用 Givens旋转法将元素M1ij(i∈[2,Lls/K],j∈[r+ 1,r+i− 1])消除为0。
(2)消除上三角操作过程:选择全0列数r相同的两个子矩阵M1和M2,矩阵中元素M1ij和M2ij i∈[2,Lls/K],j∈ [r+ 1,r+i− 1])为0;元素M1ij和M2ij(i∈[1,Lls/K],j∈ [r+ 1,r+i])非 0。以M1作为参考矩阵将矩阵M2中的元素M2ij(i∈ [1,Lls/K],j∈ [r+ 1,r+i])消除为0。完成后M1的全0列数仍为r,M2的全0列数为r+L/K。
对于第k个子矩阵Mk,如果k≤3N/(L/K)时,分解完成的条件为:前(i− 1) × (L/K)列元素全为0,且Mkij(i∈[2,Lls/K],j∈ [r+ 1,r+i− 1])为,元素Mkij(i∈[1,Lls/K],j∈ [r+ 1,r+i])非 0;k>Lls/K× 3N时,完成条件为Mk消除为全 0矩阵。
对于所有子矩阵Mk(k∈ [1,K]),持续进行消除下三角操作和消除上三角操作,直到满足分解完成条件。当所有K个子矩阵都完成分解后,依照行序号重新将子矩阵组合即可得到新的矩阵,其前3N行3N列为上三角矩阵,其余部分为0。将图1(b)中的QR分解节点替换为上述分解方法,以此构建细粒度的DAG图,完成任务模型建立。
3.2 拓扑结构模型的配置
定义 4种测试拓扑结构:Ring, Cubic,Rectangular及Cuboid如图2所示。图中每个节点表示一个处理器,处理器间的箭头线表示两个处理器间全双工的通信通道。Ring型拓扑结构硬件上由4片TS201 DSP组成,每片DSP与相邻的2片DSP通过LINK通道双向互联;Cubic型拓扑结构硬件上由8片TS201 DSP组成,每片DSP与相邻的3片DSP通过LINK通道双向互联,Cubic型可以看作是Ring型结构的扩展。Rectangular型拓扑结构硬件上8片TS201 DSP组成,相邻的DSP之间通过 LINK通道双向互联;Cuboid型硬件上由两组Rectangular型拓扑结构扩展而成。依据图2各拓扑结构中处理器的个数以及处理器间的连接关系配置拓扑结构模型TP = {U,CH}。
3.3 实验及分析
依照表1配置5组STAP处理参数,并使用DLS算法实现并行任务分配。其中实验1-实验4依据4.1节中的方法建立细粒度的DAG任务图,实验5直接使用粗粒度的DAG任务图。
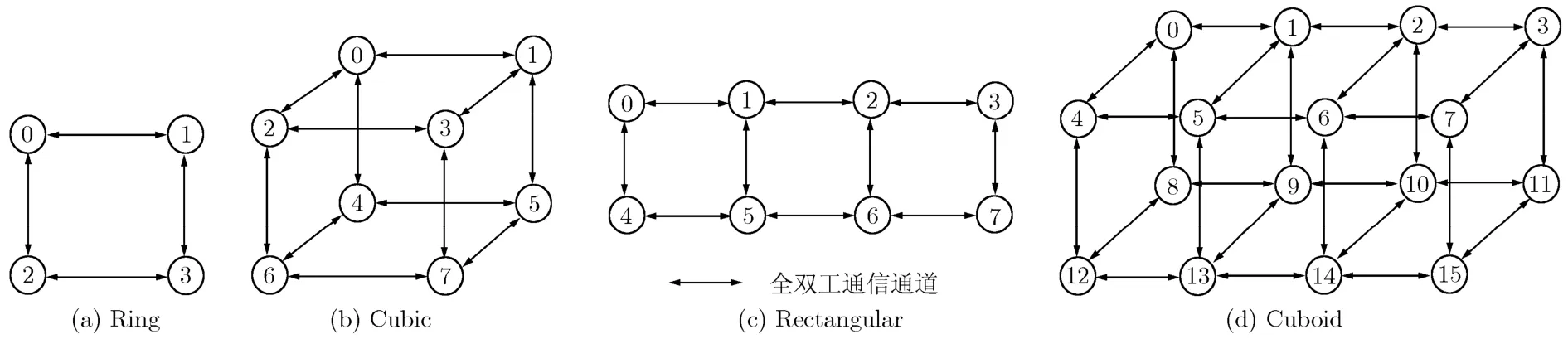
图2 拓扑结构示意图
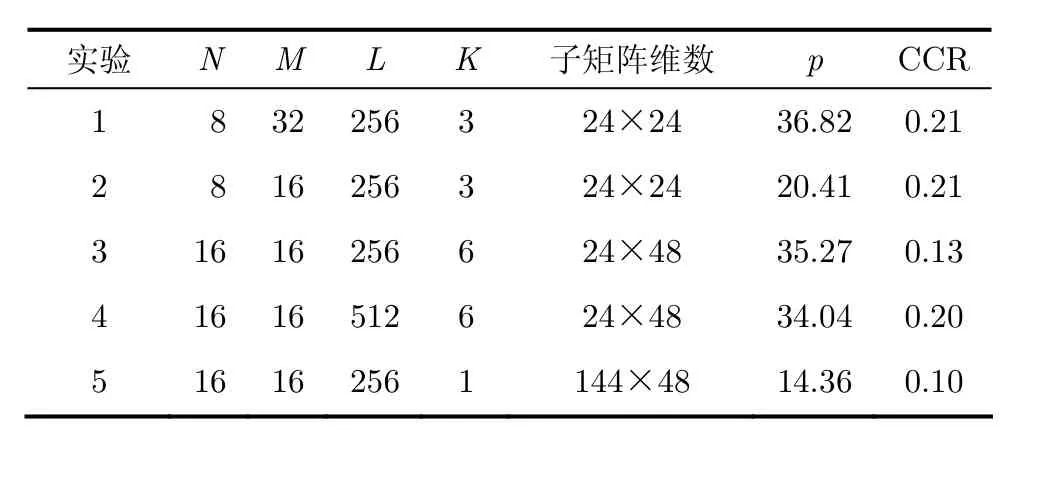
表1 STAP参数设定及p与CCR统计
通过实际测试获取各 DAG图中各任务在TS201中的实际计算开销,表2统计了TS201中各维数矩阵消除上三角与消除下三角操作的计算开销。其中实验5中QR分解分块个数K=1,因此仅需要一次消除下三角操作即可完成QR分解,故不存在消除上三角操作。根据式(1)与式(2)统计得到5个实验中 DAG的并行度p及CCR,统计如表 1所示。

表2 QR分解操作计算开销统计(μs)
由图 1(a)可以看出,M−2组权值计算之间为相对独立的过程。在实验1中M=32,需完成30组权值计算与STAP滤波,因此实验1中的并行度最高达到了36.82。对比实验3与实验5,实验3中采用细粒度的任务划分方法,并行度达到了35.27;而实验5采用粗粒度的方法,并行度仅为14.36。可以看出细粒度的任务划分虽然增加了传输开销,但是换取了并行度的有效提高。
采用细粒度任务模型后,STAP算法中各处理阶段被拆分为细粒度的计算任务与通信任务,并映射到不同的处理器交错执行,很难直接评估各处理阶段的计算开销时间与通信开销。因此一般使用加速比ACR来衡量各实验中STAP的总体并行性能,ACR由式(9)计算得出。图3给出了5组实验中DLS的ACR统计,其中每组实验都包含了Ring, Cubic,Rectangular以及Cuboid 4种不同拓扑结构下的分配测试。
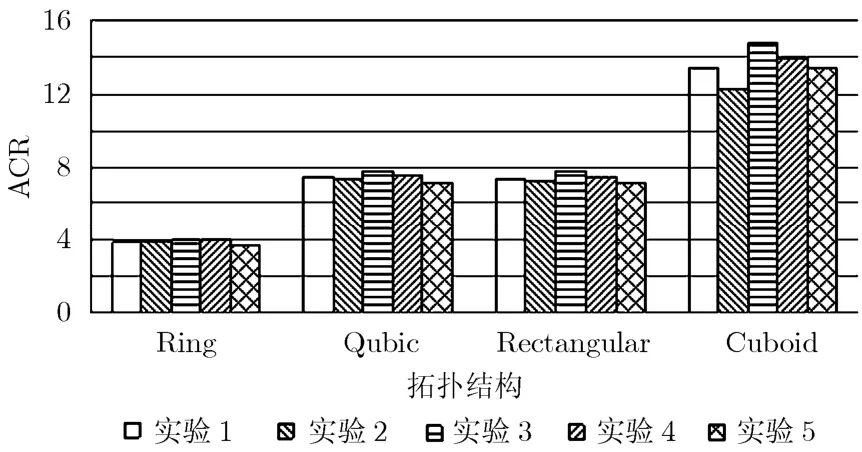
图3 ACR统计
可以看出:(1)在同一组实验中,随着拓扑结构中处理器节点个数的增加,ACR也逐步增加。(2)对比实验 1与实验 3。虽然实验 1中任务图的p= 36.82大于实验3的p= 35.27,但是实验1的CCR较大,因此在4种拓扑结构下实验3的ACR都超越了实验1。可以看出在STAP算法并行度接近的情况下,较大的通信开销将会影响并行加速性能。(3)对比实验3与实验5,在相同的系统参数配置下,细粒度任务模型具有更高的并行性,更适合于并行实现,因此达到了更优的ACR。
[7]提出了一种适用于流水处理的通用STAP并行计算模型,并给出了该计算模型下粗粒度的计算任务分配方法。该方法下的并行加速比统计见表 3。由于并行加速比与处理器的数量有直接关系,因此我们选择具有相同处理器数量的拓扑结构模型实验结果与参考文献[7]的加速比进行比较。其中4片处理器对应于本文中Ring型拓扑结构下的5组实验;8片处理器对应于本文中 Cubic与Rectangular型拓扑结构下的5组实验。结果比较如表3所示。

表3 加速比比较
由于细粒度 STAP算法本身具有很高的并行度,在处理器数量都为4的条件下,本文中Ring型拓扑结构模型的前4组实验使用了细粒度的任务模型,加速比性能要优于参考文献[7]中的加速比3.67;第5组实验使用了粗粒度的任务模型,因此加速比与参考文献[7]基本一致。
在Cubic与Rectangular下的实验中,实验1,实验3和实验4的加速比优于参考文献[7]中8片处理器的实验结果,实验2的加速性能基本与其一致。而第5组实验使用了粗粒度的任务模型,因此加速比小于参考文献[7]中的结果。
联合表1可以看出,5组实验中实验2与实验5的任务模型并行度较低,因此加速比性能较差。而实验1,实验3和实验4的任务模型并行度较高,因此在与参考文献[7]的结果比较中达到了更优的加速性能。这也再次说明,并行度越高的任务模型越适合于本文提出的STAP并行处理方法。
5组实验加载了不同的系统参数,并且每组实验都使用了4种完全不同的拓扑结构。由结果可以看出:(1)建立细粒度的任务模型提高了算法的并行度,DAG形式的任务模型适应于不同系统参数的STAP应用;(2)构建TP = {U,CH}形式的拓扑结构可以适用于不同目标硬件环境;(3)选择具有拓扑结构独立性的DLS分配算法使得整个STAP并行处理过程脱离了应用参数与系统硬件结构的限制。
4 结论
在STAP并行处理算法中,传统的并行处理方法使用粗粒度的任务划分方式,并且仅仅能够适用于特定的应用参数及硬件系统结构。粗粒度的任务划分牺牲了STAP流程的并行度;限定应用参数及硬件结构虽然易于实现,但同时也限定了传统的STAP并行处理方法的通用性。针对这些问题,本文提出了一种更具实用性的STAP并行处理方法,该方案分为以下3个步骤:建立STAP处理流程并以此构建细粒度的 DAG形式任务模型;根据实际硬件构建拓扑结构模型;基于DLS任务分配算法将任务模型中的任务分配到拓扑结构模型中的不同处理器实现STAP并行计算。
由实验结果可以看出,该并行方法能够达到良好的加速比,并且对于不同的STAP应用以及不同的硬件环境具有很好的适应性。
参 考 文 献
[1] 保铮, 廖桂生, 吴仁彪, 等. 相控阵机载雷达杂波抑制的时空二维自适应滤波[J]. 电子学报, 1993, 21(9): 1-7.
Bao Zheng, Liao Gui-sheng, Wu Ren-biao,et al.. 2-D temporal-tpatial adaptive clutter suppression for phased array airborne radars[J].Acta Electronica Sinica, 1993, 21(9):1-7.
[2] Huang Yao. A reduced-rank STAP method based on solution of linear equations[C]. Proceedings of the 2010 International Conference on Computer Design and Applications (ICCDA),Qinghuangdao, China, 2010: 235-238.
[3] Wu Ren-biao, Wang Lu, and Su Zhi-gang. Study on adaptive monopulse with reduced dimension STAP technique[C].Proceedings of the 2010 International Conference on Image Analysis and Signal Processing (IASP), Xiamen, China, 2010:159-163.
[4] 范西昆, 王永良, 陈辉. 机载雷达空时自适应处理的实时实现[J]. 电子与信息学报, 2006, 28(12): 2224-2227.
Fan Xi-kun, Wang Yong-liang, and Chen Hui. Real-time implementation of airborne radar space-time adaptive processing[J].Journal of Electronics&Information Technology, 2006, 28(12): 2224-2227.
[5] 任磊, 王永良, 陈辉, 等. STAP 并行处理系统的调度问题研究[J]. 系统工程与电子技术, 2009, 31(4): 874-880.
Ren Lei, Wang Yong-liang, Chen Hui,et al.. Research on the scheduling problems of STAP parallel processing system[J].Systems Engineering and Electronics, 2009, 31(4): 874-880.
[6] Lebak J M and Bojanczyk A W. Design and performance evaluation of a portable parallel library for space-time adaptive processing[J].IEEE Transactions on Parallel and Distributed Systems, 2000, 11(3): 287-298.
[7] 邵银波, 王永良, 李强, 等. 一种用于空时自适应处理的并行计算模型[J]. 电子学报, 2006, 34(3): 450-453.Shao Yin-bo, Wang Yong-liang, Li Qiang,et al.. A parallel computation model for space-time adaptive processing[J].Acta Electronica Sinica, 2006, 34(3): 450-453.
[8] West M and Antonio K. A genetic algorithm approach to scheduling communications for a class of parallel space-time adaptive processing algorithms[J].Journal of Parallel and Distributed Computing, 2002, 62(9): 1386-1406.
[9] Roedera M, Davisa N, Furteka J,et al.. GPU implementations for fast factorizations of STAP covariance matrices[C]. Proc. SPIE, San Diego, USA, 2008: 707403-1-707403-12.
[10] Kruatrachue B and Lewis T. Grain size determination for parallel processing[J].IEEE Transactions on Software, 1988,5(1): 23-32.
[11] Wang Chao and Liu Wei. Multi-processor task scheduling in signal processing systems[C]. Proceedings of the International Conference on Computer Science and Information Technology, Chengdu, China, 2011: 532-539.
[12] Ebaid A, Ammar R, and Rajasekaran S. Task clustering &scheduling with duplication using recursive critical path approach (RCPA)[C]. Proceedings of the 2010 IEEE International Symposium on Signal Processing and Information Technology, Luxor, 2010: 34-41.
[13] Hwang R, Gen M, and Katayama H. A comparison of multiprocessors task scheduling algorithms with communication costs[J].Computer&Research, 2008, 35(3):976-993.
[14] Sun Wei-fang, Zhu Yu-dan, Sun Zhi-yuan,et al.. A priority-Based task scheduling algorithm in Grid [C].Proceedings of the Third International Symposium on Parallel Architectures, Algorithms and Programming(PAAP), Dalian, China, 2010: 311-315.
[15] Sih G C and Lee E A. A compile-time scheduling heuristic for interconnection-constrained heterogeneous processor architecture[J].IEEE Transactions on Parallel and Distributed Systems, 1993, 4(2): 175-186.
Research on the Parallel Processing Algorithm of STAP Based on Fine-grained Task Scheduling
Wang Chao Liu Wei Yuan Pei-yuan
(School of Information and Electronics,Beijing Institute of Technology,Beijing100081,China)
In the parallelization of Space-Time Adaptive Processing (STAP) arithmetic, traditional methods schedule the STAP arithmetic to different processors in the specific hardware architecture through coral-granularity division and improve the throughput by pipeline processing between processors. In the paper, its disadvantages are discussed from two perspectives: Coarse-grained scheduling hinders the parallelism; They are only suitable for the specific system parameters and hardware architectures. Thus, a new method based on fine-grained scheduling is put forward, which consists of three steps: Firstly, fine-grained task model in the form of Direct Acyclic Graph (DAG) is constructed; Secondly, the topology model is built to describe the target system;Finally, the established task model in fine-grained manner is assigned to different processors described in model topology. The experiment of the proposed method shows that it achieves better acceleration ratio, and more flexiable adaptation to different STAP applications.
Signal processing; Space-Time Adaptive Processing (STAP) systems; Parallel processing; Task scheduling; Fine-granularity
TN911.7
A文章编号:1009-5896(2012)06-1398-06
10.3724/SP.J.1146.2011.00683
2011-07-06收到,2012-03-05改回
*通信作者:刘伟 eliuwei@bit.edu.cn
王 超: 男,1985年生,博士生,研究方向为实时信号处理.
刘 伟: 男,1976年生,讲师,研究方向为实时信号处理.
袁培苑: 女,1988年生,硕士生,研究方向为实时信号处理.

