自起动永磁同步电机起动过程电枢反应退磁分析

卢伟甫，罗应立，赵海森

(华北电力大学 电气与电子工程学院，北京102206)

0 引言

永磁电机中的电枢反应退磁磁场使得永磁体工作点磁密降低，可能导致电机的不可逆退磁，影响电机运行性能，因此研究电枢反应退磁对永磁电机的运行和设计具有重要意义。文献[1－3]采用时步有限元法计算了永磁体的工作点磁密，有助于准确分析永磁体退磁情况。文献[4－6]分析了一些非正常运行工况下较大电流如短路电流产生的电枢反应退磁磁场对永磁体工作点磁密的影响，为研究永磁电机各种电枢反应退磁情况提供了必要的依据。但上述文献多是对某一静态时刻电枢电流对永磁体退磁的影响分析，对起动过程中电枢反应动态退磁特点研究的较少。自起动永磁同步电机(line－start permanent magnet synchronous motor，LSPMSM)起动过程中，电枢同步旋转磁场与永磁磁场的相对位置不断变化，当两磁场方向相反时，电枢磁动势对永磁体的去磁作用较严重[7－8]，因此有必要重点分析LSPMSM起动过程中的电枢反应退磁对永磁体工作点磁密的影响。

LSPMSM起动过程中各个时刻永磁体内平均工作点磁密的大小，既与电枢同步旋转磁场和转子永磁磁场的相对位置有关，又与电枢电流的幅值有关。因此本文采用场－路－运动耦合的时步有限元法，以某22 kW自起动永磁同步电机为例，分析了电枢同步旋转磁场与永磁磁场相对空间位置角δ与电枢磁场强弱对永磁体工作点磁密的影响，得到不同负载条件下起动过程中的电枢反应退磁特点，为进一步深入开展永磁电机抗退磁方面的研究提供了必要的理论参考。

1 电枢反应退磁时步有限元模型和计算方法

为分析自起动永磁同步电机起动过程中的电枢反应退磁，以一台22 kW 8极LSPMSM为例，其参数见表1，1对极下的模型如图1所示。

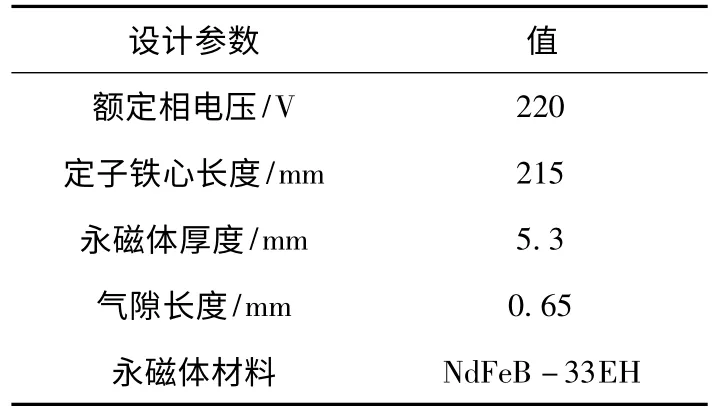
表1 22 kW LSPMSM参数Table 1 Parameters of LSPMSM of 22 kW

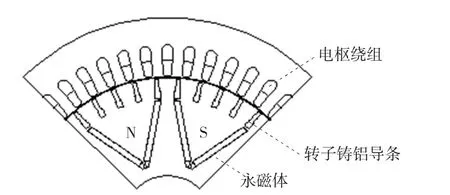
图1 LSPMSM四分之一模型图Fig.1 Quarter model of LSPMSM

为了准确分析电枢反应退磁磁场对永磁体工作点磁密的影响，本文采用能够计及饱和、集肤效应等多种因素影响的时步有限元法，计算自起动永磁同步电机内永磁体各个剖分单元不同时刻的工作点磁密。

永磁电机电磁场瞬态边值问题，可表示为[9]

式中:A为矢量磁位，Js为传导电流密度;μ为磁导率，σ为电导率;v1，v2为不同介质的磁阻率;δc为永磁体等效面电流密度，δc=Hc×n，其中 Hc为永磁体矫顽力，n为永磁体边界外法向单位矢量;G为求解区域;Γ1为定子铁心外圆边界;Γ2为永磁体和其他媒介的交界。

将式(1)的电磁场边值问题离散并联立电路方程、运动方程得到永磁电机的场－路－运动耦合方程[10－11]，直接求解便可得到节点磁位、转子位置、电枢电流以及永磁体单元磁密等信息。为准确反映永磁体工作点磁密，本文将永磁体细剖分，单元格式如图2所示。经计算分析表明，永磁体绝大部分单元的磁密随时间的变化趋势一致。因此将各时刻的永磁体单元磁密求取平均，作为该时刻的永磁体平均工作点磁密，以反映起动过程中电枢反应退磁。

图2 永磁体单元剖分Fig.2 Permanent magnet element subdivision

2 起动过程中电枢反应退磁特点

2.1 空载起动过程中电枢反应退磁特点

自起动永磁同步电机起动过程中，电枢同步旋转磁场(以电压相位角为参考)超前转子永磁磁场(以转子位置角为参考)的空间电角度用δ表示[12]，其余弦值为 cosδ。当 －π/2＜δ＜π/2(即 cosδ＞0)时，电枢磁场对永磁体起增磁作用，永磁体内磁密增大;当 π/2＜δ＜3π/2(即 cosδ＜0)时，电枢磁场对永磁体起去磁作用，永磁体内磁密减小;且δ=π(即cosδ=－1)时，去磁作用较强，永磁体平均工作点磁密较低。

首先以样机的空载起动为例，采用时步有限元法计算得到空载起动转速如图3(a)所示，转子永磁磁场转过的累计角度与电枢同步旋转磁场转过的累计角度如图3(b)所示，两者的空间位置电角度之差 δ如图3(c)所示。图4为 δ的余弦值cosδ，图5为永磁体平均工作点磁密随时间的变化曲线。

图3 空载起动过程中转速、电枢磁场与永磁磁场相对位置Fig.3 Speed，the relative position between armature magnetic field and permanent magnetic field during no-load start process

图4 相对位置角的余弦值cosδFig.4 Cosine value of relative position angle

由图3～图5可见，cosδ的正、负分别表明了电枢磁场的增、去磁作用，而|cosδ|越大，电枢磁场对永磁体的作用越大。增磁时，作用越大，永磁体平均工作点磁密越高;反之，去磁时，作用越大，永磁体平均工作点磁密越低。如图4中的点 a和 b，分别对应cosδ=1和cosδ= －1。相应的，图5中的点 a，磁密增大到约0.85 T;图5中的点 b，磁密降低到约0.2 T。

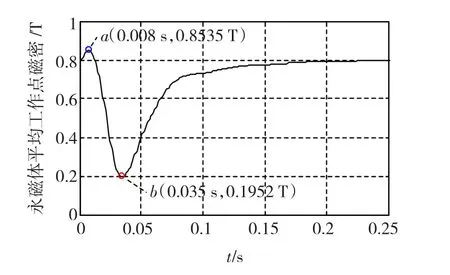
图5 空载起动过程中永磁体平均工作点磁密Fig.5 Permanent magnet＇s average working point flux density during no-load start process

以上分析可见，样机空载起动很快完成，永磁体只经历了一次δ=π(即cosδ=－1)的时刻，永磁体平均工作点磁密出现一次较低点，当该点低于永磁材料退磁曲线的拐点时，将产生不可逆退磁。

2.2 重载起动过程中电枢反应退磁特点

样机带额定负载起动时，计算得到转速、定子电流、cosδ以及永磁体平均工作点磁密，如图6(a)～图6(d)所示。其中图6(b)为定子A相电流及三相电流合成的向量幅值曲线。

由图6可见，在重载条件下起动，电机起动时间长，永磁体多次经历电枢磁场与永磁磁场反相即cosδ=－1的时刻，因此永磁体工作点磁密多次出现较低点。

在转子转速较低时，定子起动电流幅值较大，因此电枢绕组阻抗压降较大，电枢绕组感应电动势幅值较小，定、转子电流合成磁场相对较弱，相应的电枢磁动势对永磁磁动势的影响较小;随着转速升高，电流幅值减小，在最后一个接近同步速的cosδ=－1时刻(如图6(c)中的点c)，电枢磁场对永磁磁场的去磁作用最强，使得永磁体平均工作点磁密达到额定负载起动过程中的最低点，如图6(d)中的点 c。

以上分析表明，重载起动时间长，永磁体磁密多次出现较低点，退磁几率变大，且在最后一个电枢磁场与永磁磁场反相位置，永磁体平均工作点磁密最低，电枢反应退磁较严重。

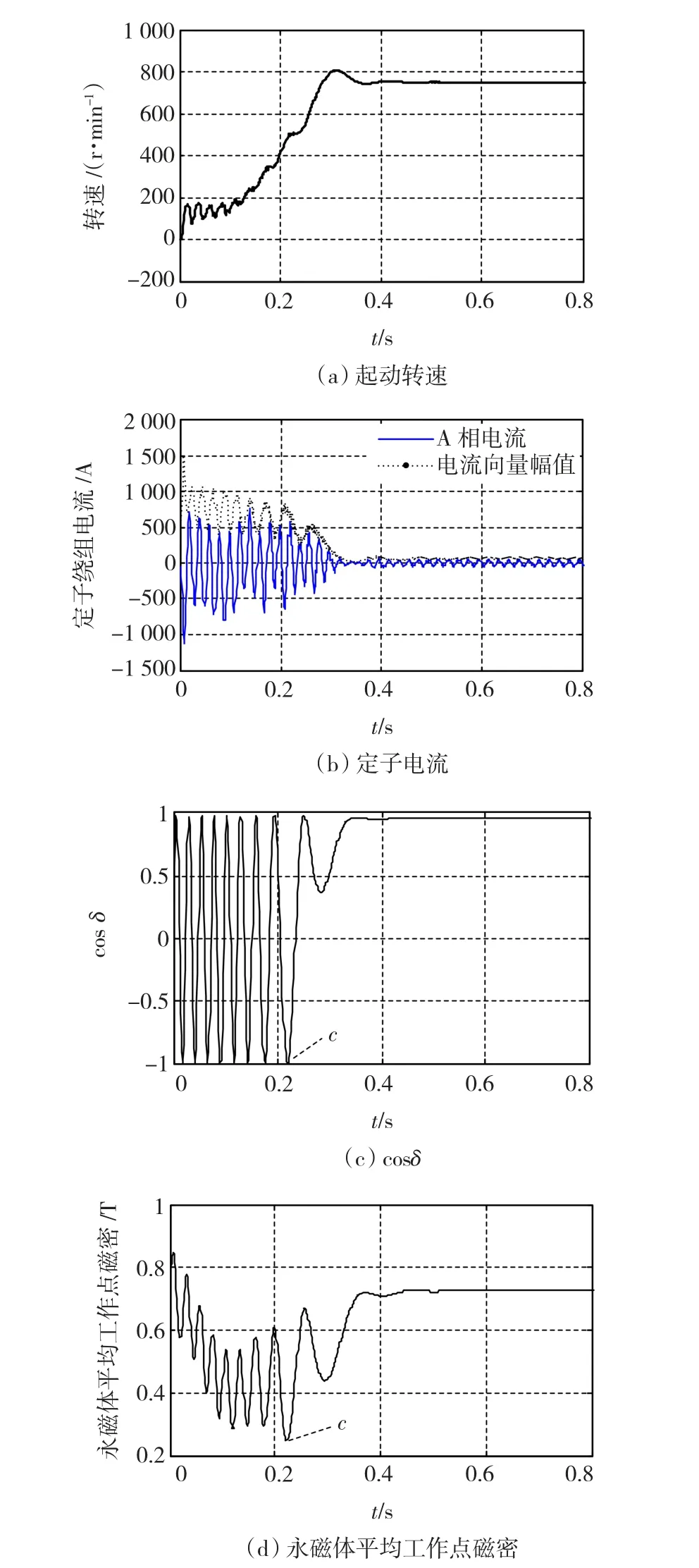
图6 额定负载起动过程中的转速、定子电流、cos δ及永磁体磁密Fig.6 Speed，stator currents，cos δ and the permanent magnet flux density during rated-load start process

3 不同负载起动过程中的电枢反应退磁特点比较和分析

为进一步分析比较不同负载条件下电枢反应退磁特点，图7(a)～图7(d)分别比较了不同负载条件下起动过程中的转速、定子电流向量幅值、cosδ和永磁体平均工作点磁密。图8为不考虑永磁磁场，只考虑外施电压所产生的定子电流与转子鼠笼导条感应电流共同产生的鼠笼异步电机效应磁场作用下的永磁体区域磁密，具体计算模型参见文献[11]。

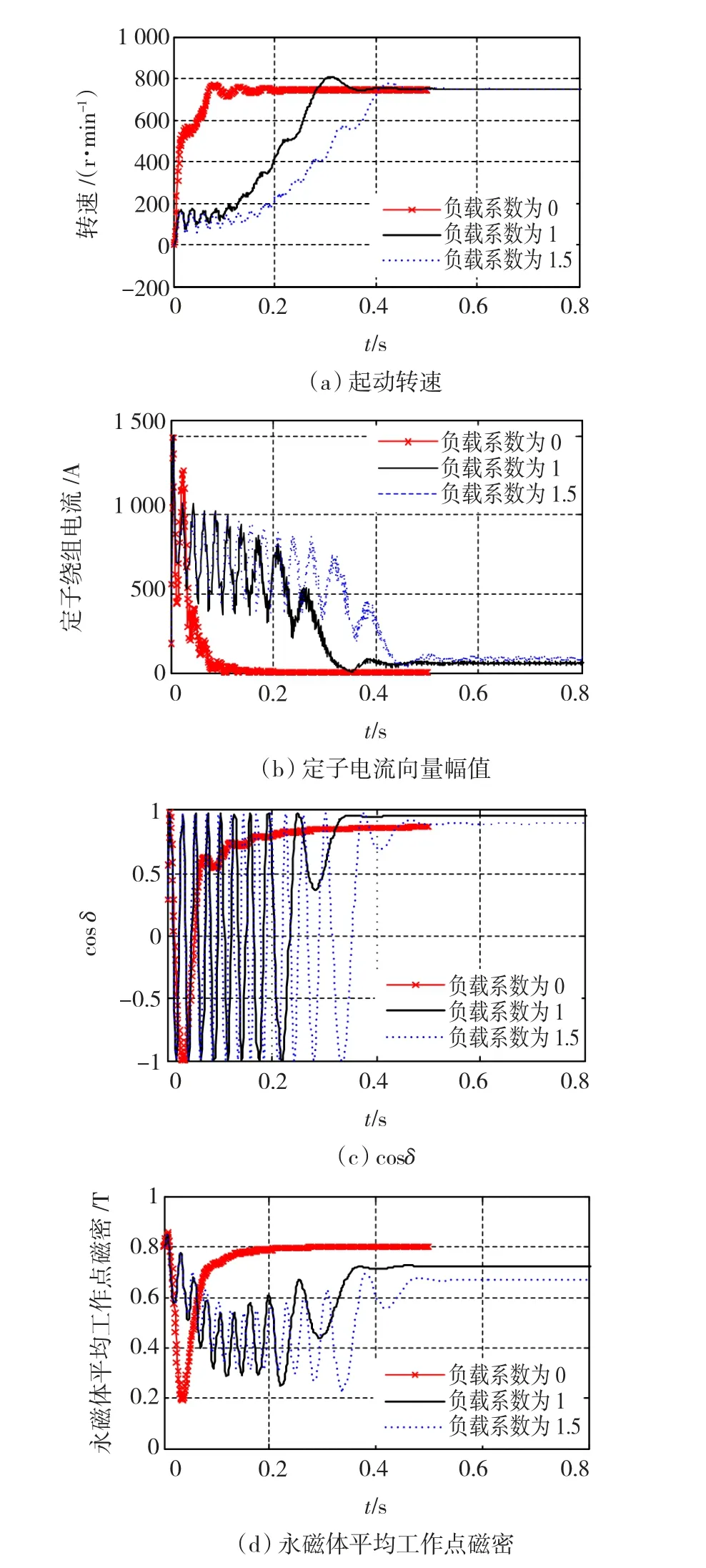
图7 不同负载起动过程中的起动性能及永磁体磁密Fig.7 Starting performance and the permanent magnet flux density during the start process under different loads

由图8起动过程中鼠笼异步电机效应磁场对永磁体区域磁密的影响可见，随着负载系数增加，起动时间变长，电枢磁场与永磁体的相对空间位置角δ导致永磁体区域的磁密出现多次正负交变。且随着转速升高，电流幅值减小，相应的电枢绕组感应电动势增大，对应的气隙磁密增大，永磁体区域磁密波动幅值逐渐增大，在δ=π时刻永磁体区域磁密也就越低。起动完成后，永磁体区域磁密稳定于一个恒值不变。由图7(b)、图7(c)可见，在不同负载条件下稳定运行时的空间位置差电角度基本相同，而负载越大，稳定电流幅值越大，相应的感应电动势越小，对应的气隙磁密越小，从而稳定时永磁体区域磁密越低。

图8 不同负载起动过程中，鼠笼异步电机效应磁场作用下的永磁体区域磁密Fig.8 Permanent magnet flux density considering asynchronous effect alone during the start process under different loads

由图8所示的鼠笼异步电机效应磁场对永磁体区域的影响直接导致了如图7(d)所示的不同负载条件下起动过程中永磁体平均工作点磁密波动变化的特点。

4 结论

本文以一台22 kW自起动永磁同步电机为例，采用场－路－运动耦合的时步有限元法分析了起动过程中电枢磁场与永磁磁场相对空间位置角δ与电枢电流幅值对永磁体工作点磁密的影响，得到了不同负载条件下起动过程中电枢反应退磁特点。

1)当－π/2＜δ＜π/2时，电枢磁场对永磁体起增磁作用，永磁体内磁密增大;当 π/2＜δ＜3π/2时，电枢磁场对永磁体起去磁作用，永磁体内磁密减小，且δ=π时，去磁作用较强，永磁体平均工作点磁密较低。

2)负载系数越大，起动过程中永磁体经历较低磁密点的次数越多，永磁体退磁几率变大;随着转速升高，电枢电流幅值减小，在最后一个接近同步速的δ=π时刻，永磁体磁密出现最低点;且稳定时负载系数越大，电流幅值越大，永磁体稳定平均工作点磁密越小。

[1]RUOHO S，DLALA E，ARKKIO A.Comparison of demagnetization models for finite-element analysis of permanent-magnet synchronous machines[J].IEEE Transactions on Magnetics，2007，43(11):3964－3968.

[2]ZHOU P，LIN D，XIAO Y，et al.Temperature-dependent demagnetization model of permanent magnets for finite element analysis[J].IEEE Transactions on Magnetics，2012，48(2):1031 －1034.

[3]郭伟，张承宁.车用永磁同步电机的铁耗与瞬态温升分析[J].电机与控制学报，2009，13(1):83 －87，92.GUO Wei，ZHANG Chengning.Iron losses and transient temperature analysis of the permanent magnet synchronous motor for electric vehicles[J].Electric Machines and Control，2009，13(1):83－87，92.

[4]ROSU M，SAITZ J，ARKKIO A.Hysteresis model for finite-element analysis of permanent-magnet demagnetization in a large synchronous motor under a fault condition[J].IEEE Transactions on Magnetics，2005，41(6):2118 － 2123.

[5]KIM Kichan，LIM Seungbin，KOO Daehyun，et al.The shape design of permanent magnet for permanent magnet synchronous motorconsidering partial demagnetization[J].IEEE Transactions on Magnetics，2006，42(10):3485 －3487.

[6]WANG J，WANG W，ATALLAH K，et al.Demagnetization assessment for three-phase tubular brushless permanent-magnet machines

[J].IEEE Transactions on Magnetics，2008，44(9):2195 －2203.

[7]唐任远.现代永磁电机理论与设计[M].北京:机械工业出版社，1997:185－188.

[8]王秀和，杨玉波，朱常青.异步起动永磁同步电动机[M].北京:机械工业出版社，2009:159－161.

[9]胡敏强，黄学良.电机运行性能数值计算方法及其应用[M].南京:东南大学出版社，2003:170－177.

[10]张健，罗应立，陈伟华，等.自起动永磁电机最小转矩的时步有限元计算[J].电机与控制学报，2011，15(3):80 －85.ZHANG Jian，LUO Yingli，CHEN Weihua，et al.Calculation of line-start permanent magnet motor minimal torque based on timestepping finite element method [J].Electric Machines and Control，2011，15(3):80 －85.

[11]卢伟甫，刘明基，罗应立，等.自起动永磁同步电机起动过程退磁磁场的计算与分析[J].中国电机工程学报，2011，31(15):53－60.LU Weifu，LIU Mingji，LUO Yingli，et al.Demagnetization field analysis and calculation for line-start permanent magnet synchronous motor during start process[J].Proceedings of the CSEE，2011，31(15):53 －60.

[12]李志强.自起动永磁电机动态过程的有限元分析与实验研究[D].北京:华北电力大学，2009.