三相无轴承异步电机的磁场定向控制

卜文绍，乔岩珂，祖从林，黄声华

(1.河南科技大学 电子信息工程学院，河南 洛阳471003;2.洛阳矿山机械工程设计研究院，河南 洛阳471039;3.华中科技大学 电气与电子工程学院，湖北 武汉430074)

0 引言

无轴承电机是利用相差一对磁极的悬浮磁场叠加于电机旋转气隙磁场，通过改变电机合成气隙磁场的分布，从而控制作用在转子上的麦克斯韦电磁力的大小和方向，实现悬浮控制的[1－6]。电机的电磁转矩和磁悬浮力之间存在着基于四极转矩系统气隙磁场的耦合关系，如果能有效控制转矩绕组产生气隙磁场的幅值大小和相位，不但输出转矩不会受悬浮绕组的影响，而且能精确计算电磁悬浮力及其控制电流的大小[1－2，6－8]。转矩系统气隙磁链定向的准确性对悬浮控制性能的影响较大，它直接影响到悬浮力分量之间的解耦特性。因此，如何准确获取转矩系统气隙磁链的相位信息，是实现电磁转矩和磁悬浮力之间，以及两磁悬浮力分量之间可靠解耦控制的关键。

关于无轴承异步电机控制，国内外已有不少研究成果[1－18]。本文将对无轴承异步电机转矩系统的磁场定向控制方法、悬浮控制系统的转子感应补偿问题等进行分析;然后根据电机的运行特点选择适当的磁场定向控制策略，对三相无轴承异步电机的控制系统进行仿真和实验研究。

1 四极转矩系统的磁场定向控制

1.1 电机磁场定向控制的基本模型

在dq同步旋转坐标系中，磁场定向数学模型包括电压方程、磁链方程和转矩方程等。

电压方程:

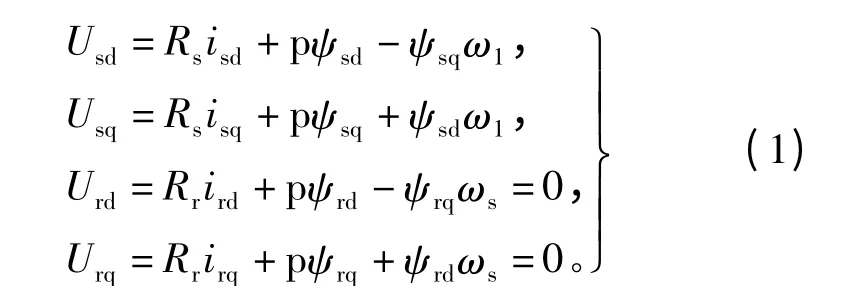
式中:ω1是电机磁场的同步电角速度;ωs是转差电角频率;Usd和Usq分别为转矩绕组的 d、q轴电压分量;Urd和Urq分别为转子绕组的d、q轴电压分量;Rs和Rr分别为定、转子绕组的电阻，p为微分算子。

磁链方程:

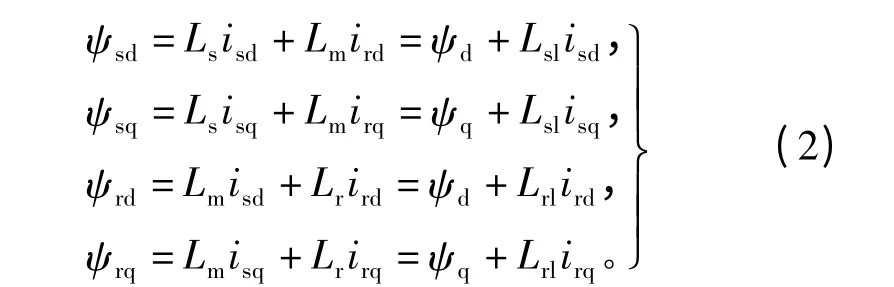
其中:ψd和ψq分别为四极转矩系统定转子合成气隙磁链的d轴和q轴分量，即

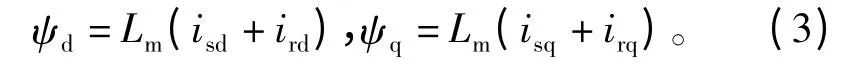
式中:Lm为dq坐标系中定子与转子同轴等效绕组间的互感;Ls为dq坐标系中定子等效两相绕组的自感，Ls=Lm+Lsl;Lr为dq坐标系中转子等效两相绕组的自感，Lr=Lm+Lrl;Lsl和 Lrl分别为定转子绕组的漏电感;isd和isq为定子电流的d、q轴分量;ird和irq为转子电流的d、q轴分量。

转矩方程:

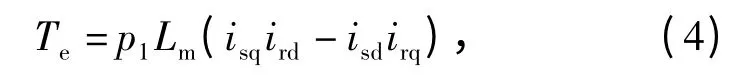
式中:p1为转矩绕组的极对数。

把式(2)带入式(1)，可得

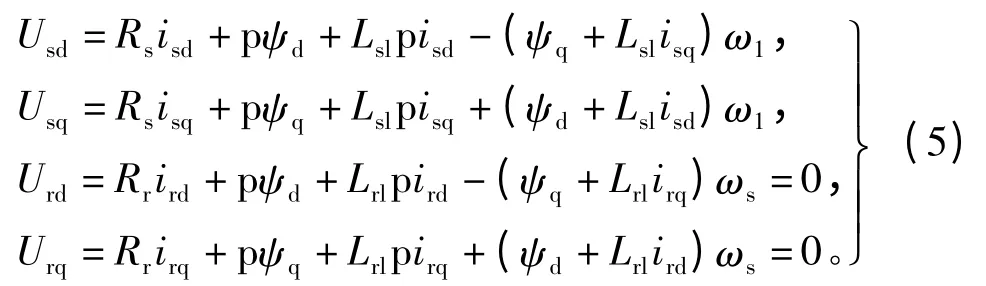
因电机的定子磁场、转子磁场、气隙磁场都以同步速旋转，根据“d”坐标轴所选取的基准方向不同，转矩系统有多种磁场定向控制方式。

1.2 四极转矩系统的气隙磁场定向控制

气隙磁场定向时，dq同步旋转坐标系的d坐定向于四极合成气隙磁链方向上，有

联立求解式(3)、式(5)和式(6)，可得

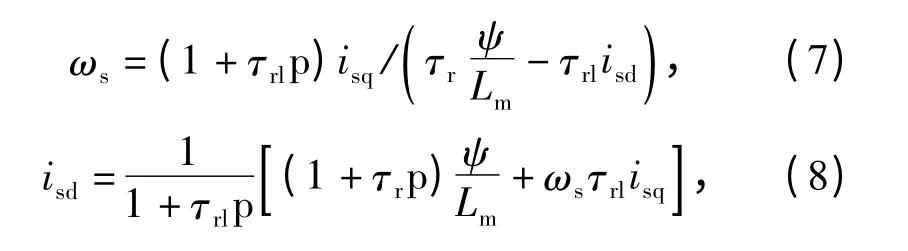
或

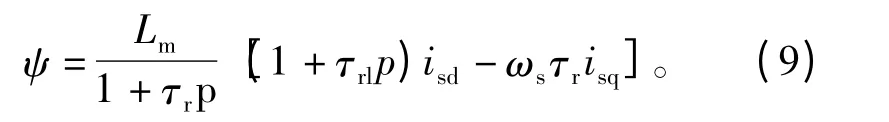
其中:τr=Lr/Rr，为转子自感时间常数;τrl=Lrl/Rr，为转子漏感时间常数。

从式(8)和式(9)可看出，定子电流的激磁分量和转矩分量没有实现解耦，激磁电流会受到转矩电流分量的影响;而且，气隙磁链算式较复杂，实时计算量大，不便于实时控制。

将式(6)代入式(3)，得

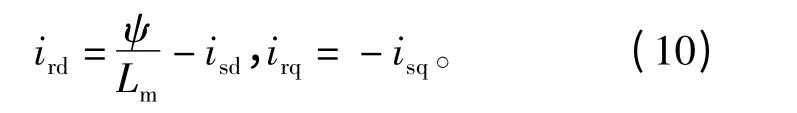
把式(10)带入式(4)，可得气隙磁场定向控制时的电磁转矩算式为

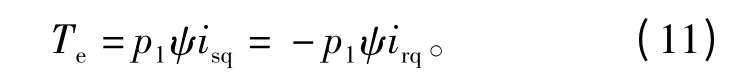
图1为转矩系统气隙磁场定向算法结构图。

根据异步电机同步旋转dq坐标系中的T型等效电路，可以得到以下关系[5]

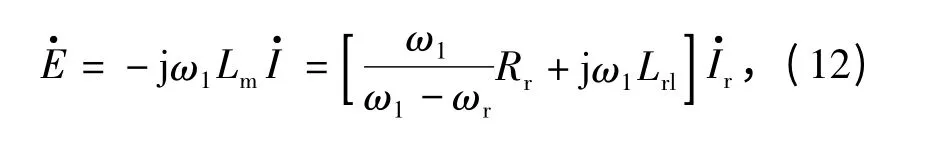
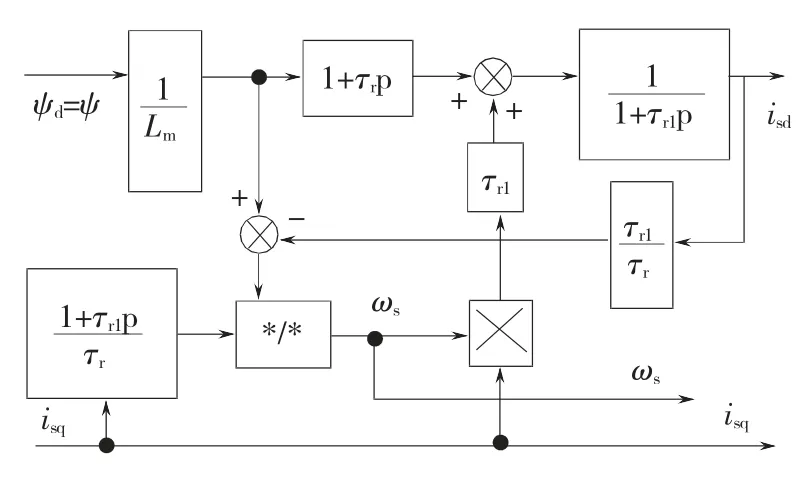
图1 转矩系统间接气隙磁场定向控制器Fig.1 Indirect air gap flux orientation controller of torque system

把合成气隙磁场表达式(3)和磁场约束条件(6)联合带入式(12)，整理得

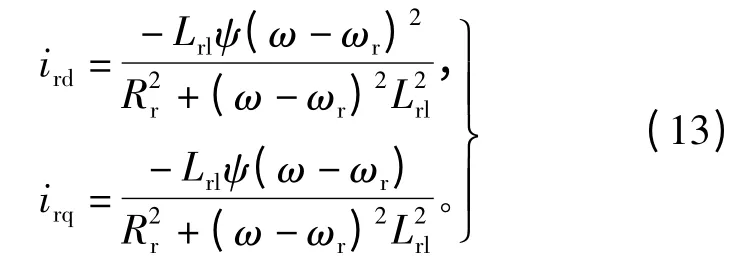
把转子绕组的转矩电流分量irq带入电磁转矩公式(11)，得

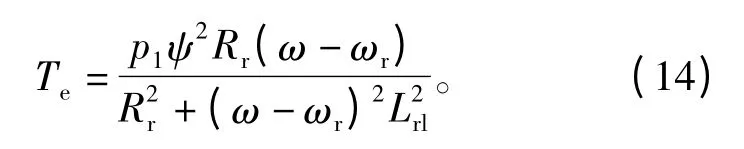
从式(14)看出:采用气隙磁场定向控制策略时，由于转子绕组漏电感的存在，电磁转矩与转差速率之间成非线性关系。

根据式(14)，把电磁转矩对电机转速求导，可得到临界限制转矩和临界转速为

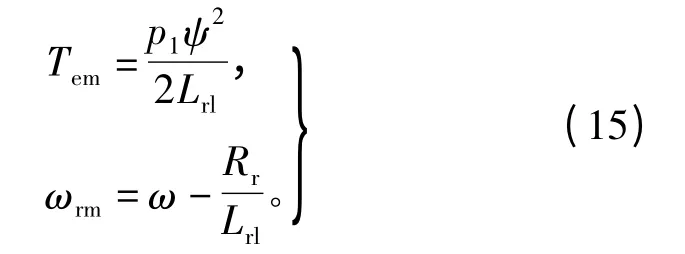
带式(15)入式(11)转矩电流表达式，可得到产生最大转矩时的转矩电流为

由式(9)、式(14)和式(15)，并结合无轴承电机的磁悬浮控制原理，可归纳出采用转矩系统气隙磁场定向控制时的以下特点:

1)转矩系统的气隙磁链幅值可以得到直接控制，气隙磁场的相位也可以根据转子旋转位置和转差角度进行准确的实时计算，因而便于转子磁悬浮力的实时解耦计算和控制;

2)因转子漏磁场储能的影响，造成了气隙磁场定向控制时机械特性随转差的非线性变化，而且存在最大转矩限制;

3)因气隙磁链受激磁电流分量 isd和转矩电流分量isq的双重影响，所以不能实现气隙磁链和定子转矩电流分量之间的解耦控制。也即，在保持气隙磁场恒定时，不能实现激磁和转矩电流分量之间的独立控制。

1.3 四极转矩系统的转子磁场定向控制

把同步旋转坐标系的“d”轴定向在转矩系统的转子磁链轴线上，磁链的约束条件为

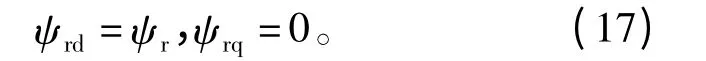
根据式(1)～式(5)和式(17)，可得转矩系统的电流、转差角频率以及电磁转矩表达式分别为

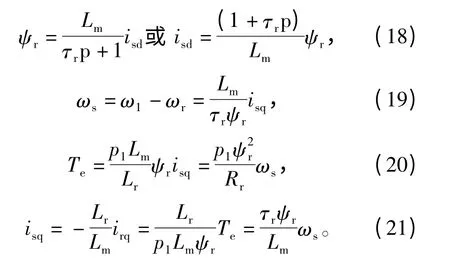
图2为对应的转子磁场定向算法结构图。

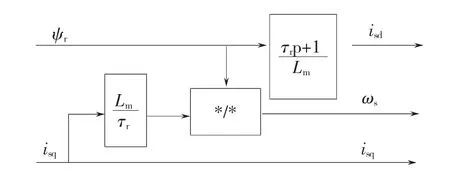
图2 转矩系统转子磁场定向控制器Fig.2 Rotor flux orientation controller of torque system

根据式(2)和式(17)，可得到气隙磁通链的计算表达式为

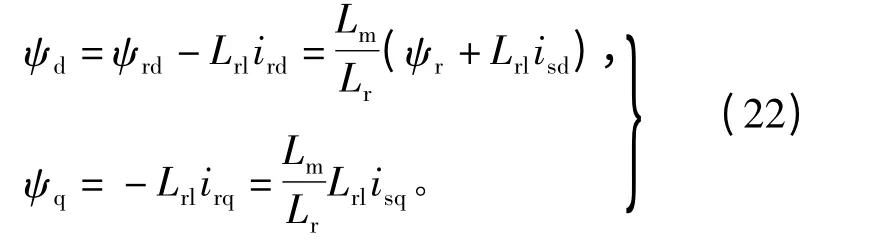
从图2以及式(18)～式(22)，可看出采用转子磁场定向控制时的以下特点:

1)转子磁链只受激磁电流isd控制，可实现激磁电流分量 isd和转矩电流分量 isq之间的完全解耦控制;

2)可通过调节转矩电流isq实现电磁转矩的线性调节，且不存在气隙磁场定向控制时的最大电磁转矩限制的问题;

3)电机合成气隙磁场将随电机定子电流的变化而变化，为实现磁悬浮系统的解耦控制，需要实时计算转矩系统的气隙磁链幅值和相位。

根据式(22)，可得到气隙磁链的幅值及其偏离转子磁链的电角度分别为

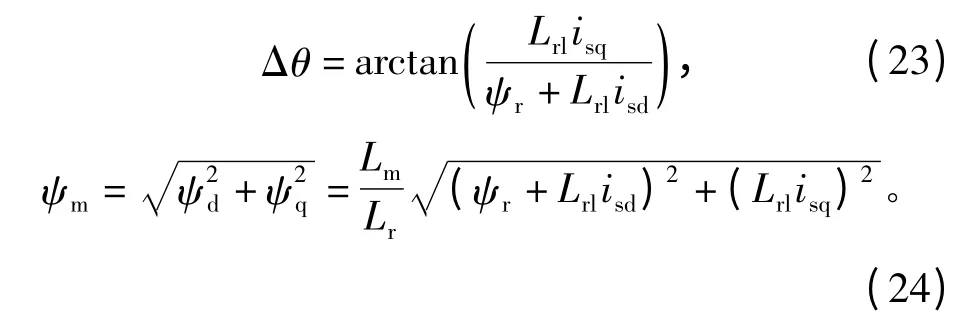
在电流不是很大的情况下，漏感磁链相对于转子磁链ψr很小，可以忽略，则有近似算式为

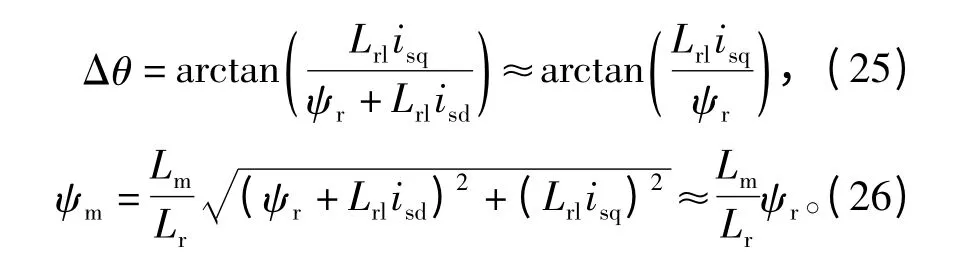
2 磁悬浮系统的磁场定向策略及感应补偿

无轴承电机的悬浮力是通过转矩系统和悬浮系统之间气隙磁场的相互作用而产生的;转矩系统除要产生基波磁场外，还要产生电磁转矩;而产生所需大小和相位的悬浮控制磁场，却是悬浮控制系统的唯一任务。所以，悬浮控制系统一般采用气隙磁场定向控制策略，其磁场定向控制算法与转矩系统类似，仅磁极对数有所不同而已，此处不予详述。

若转子绕组未做固定磁极对数处理，则旋转的悬浮控制磁场将在其中产生感应电流。在电机稳定运行时，转子径向偏心位移一般远小于电机的平均气隙。若忽略因转子微弱偏心引起的两套绕组间的互感耦合，从悬浮绕组的电枢电流到控制(激磁)电流的传递函数为[10]

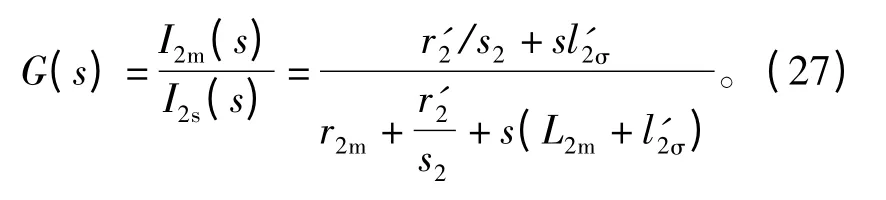
对应的频率特性可表示为

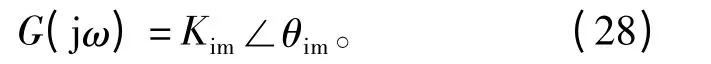
其中，幅频和相频特性可表示为

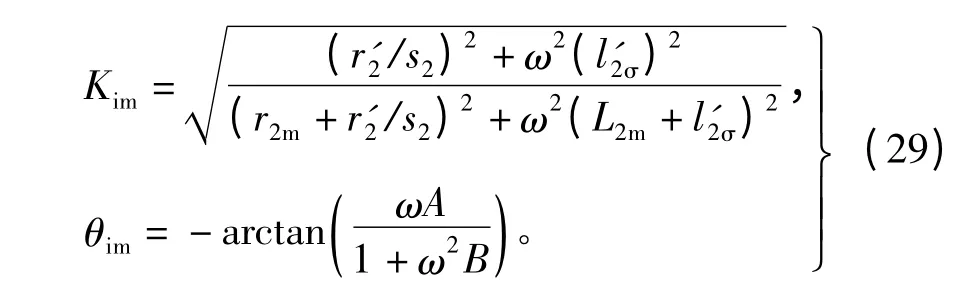
式中:

式(28)～式(30)表明:由于磁悬浮系统的转子感应，悬浮控制(激磁)电流与悬浮绕组电枢电流之间不但存在幅值偏差，还存在相位偏差。若把电枢电流的两个分量i2sm和i2st当作“期望的”磁悬浮控制(激磁)电流，必将导致两静止坐标轴向磁悬浮力分量之间的耦合。

为克服二极磁悬浮控制系统的转子感应影响，需要采用幅相补偿环节，以改善控制性能。

可取校正环节:

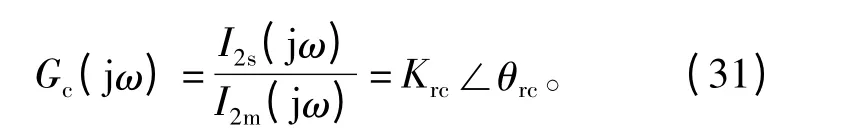
其中，幅值和相角补偿算式为

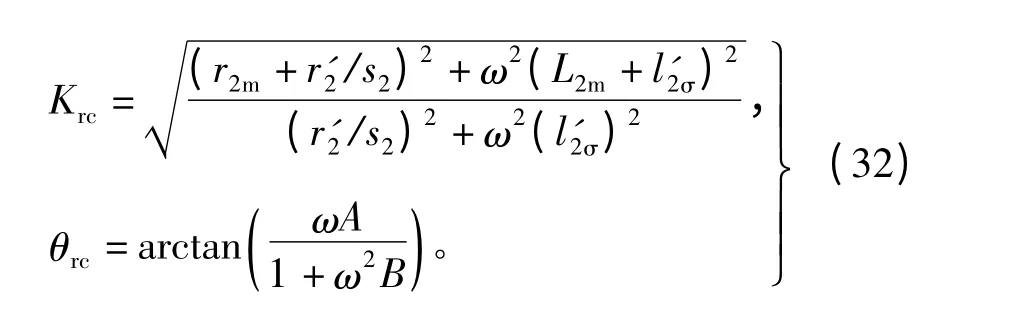
根据幅值和相位校正关系，磁磁悬浮控制(激磁)电流命令信号到磁悬浮绕组电枢电流命令信号的幅相“超前”补偿关系可表示为

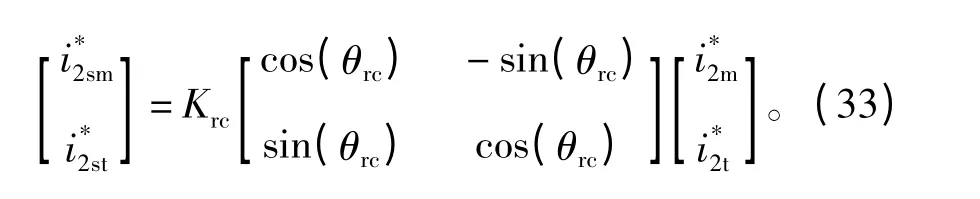
其中:

3)Krc为串联校正环节的幅值放大倍数，θrc为串联校正环节的“超前补偿角”。

3 系统仿真与实验

根据前面分析，无论转矩系统采用转子磁场定向或气隙磁场定向，都不能同时兼顾转矩控制和悬浮控制同时具有最佳性能。从悬浮控制及计算的便利性角度考虑，应选气隙磁场定向控制;而从电机的驱动控制性能角度看，应选转子磁场定向控制。鉴于转子磁场定向控制相对简单的矢量控制算法、优良的调速特性等特点，四极转矩系统采用了转子磁场定向控制策略，同时根据转矩绕组的漏电感和绕组电流来实时计算气隙磁场的相位偏差角度和气隙磁链幅值信息，以便为磁悬浮力的实时解耦计算和控制提供依据;二极磁悬浮控制系统则采用气隙磁场定向控制，同时对转子绕组进行幅相感应补偿。

本文针对二极悬浮控制四极无轴承异步电机样机的控制系统进行仿真和实验研究，电机功率为2 kW。首先基于 Matlab/Simulink仿真软件，对无轴承异步电机的磁场定向解耦控制系统进行了仿真研究。图3为三相无轴承异步电机磁悬浮解耦控制系统的仿真波形;图3(a)给出的是电机转速变化波形，除起动过程中略有波动外，电机转速始终保持在给定值;图3(b)和图3(c)分别给出了沿 α和 β静止坐标轴向的转子径向位移变化波形。图4给出的是稳态下三相无轴承异步电机磁悬浮解耦控制系统的实时径向位移变化波形。从仿真和实验结果可看出，在电机转矩系统采用转子磁场定向控制，并实时计算气隙磁场信息，悬浮系统采用气隙磁场定向控制加感应补偿的组合控制策略下，电机实现了稳定的悬浮控制。图5中转子径向位移的周期性波动缘于转子质量不平衡;关于转子不平衡振动控制方法，将在后续研究中进一步给出。

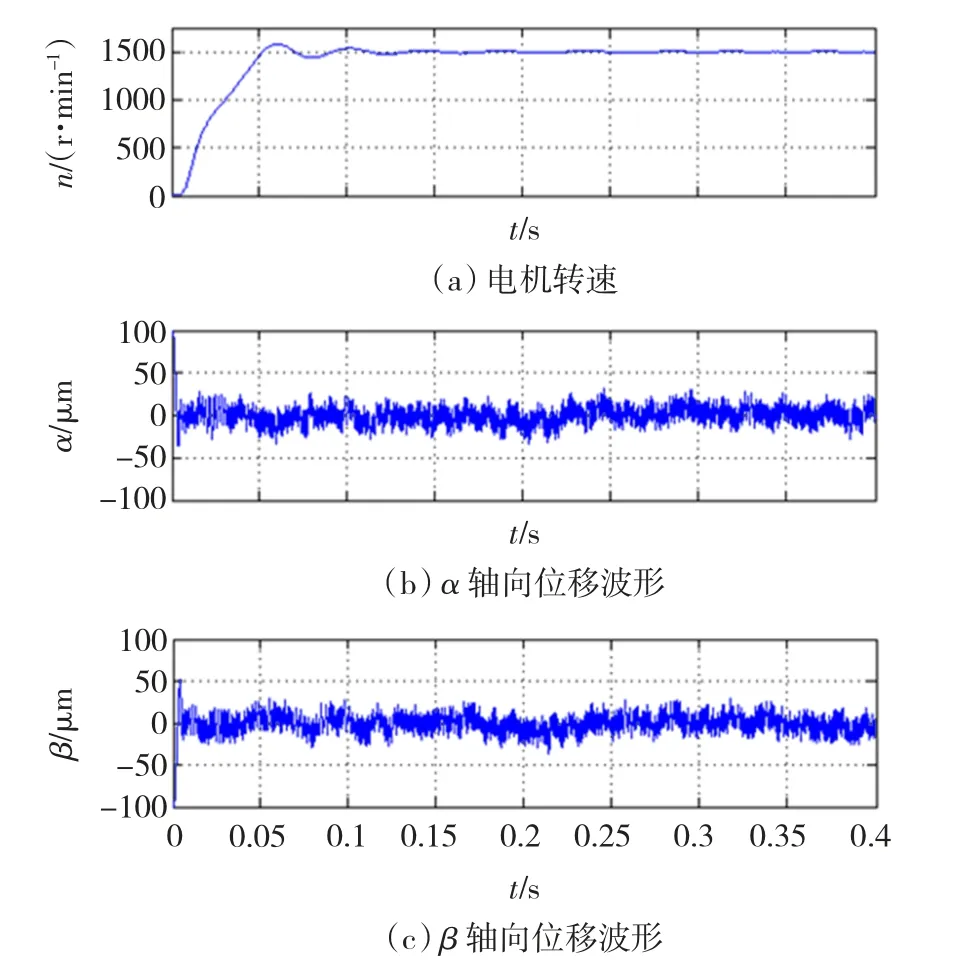
图3 磁悬浮解耦控制系统仿真波形Fig.3 Simulink waves of magnetic suspension decoupling control system

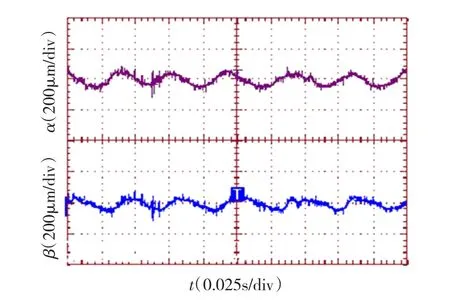
图4 磁悬浮解耦控制径向位移实验波形Fig.4 Experimental waves of radial displacement for magnetic suspension decoupling control system

4 结语

本文对无轴承异步电机转矩系统的四极气隙磁场定向控制策略和转子磁场定向控制策略进行了对比分析，介绍了二极磁悬浮控制系统的转子感应补偿方法;然后结合无轴承异步电机的运行控制特点，四极电机转矩系统采用了转子磁场定向控制，二极磁悬浮系统采用了气隙磁场定向控制加幅相感应补偿的组合控制策略，对三相无轴承异步电机磁悬浮解耦控制系统进行了仿真和实验研究。仿真和实验结果表明了本文所采用的磁场定向控制控制策略和感应补偿方法的有效性。

[1]邓智泉，王晓琳，张宏荃，等.无轴承异步电机的转子磁场定向控制[J].中国电机工程学报，2003，23(3):89－92.DENG Zhiquan，WANG Xiaolin，ZHANG Hongquan，et al.The nonlinear control of bearingless induction motors based on the motor rotor flux orientation[J].Proceedings of the CSEE，2003，23(3):89－92.

[2]贺益康，年珩，阮秉涛.感应型无轴承电机的优化气隙磁场定向控制[J].中国电机工程学报，2004，24(6):116－121.HE Yikang，NIAN Heng，RUAN Bingtao.Optimized air-gap-flux orientatied control of an induction-type bearingless motor[J].Proceedings of the CSEE，2004，24(6):116－121.

[3]黄燕，王晓琳，仇志坚，等.交替极无轴承电机的转矩与悬浮特性[J].电机与控制学报，2010，14(12):91 －95.HUANG Yan，WANG Xiaolin，QIU Zhijian，et al.Characteristics of torque and suspension force in a consequent-pole bearingless motor[J].Electric Machines and Control，2010，14(12):91－95.

[4]蔡国洋，黄守道.无轴承异步电机气隙磁场辨识方法与应用[J].电机与控制学报，2007，11(2):116 －120.CAI Guoyang，HUANG Shoudao.The air gap field identification methods and application of bearingless induction motors[J].Electric Machines and Control，2007，11(2):116 －120.

[5]王晓琳，邓智泉.无轴承异步电机磁场定向控制策略分析[J].中国电机工程学报，2007，27(27):77 －82.WANG Xiaolin，DENG Zhiquan.Analysis of Flux-oriented strategies of bearingless asynchronous motor[J].Proceedings of the CSEE，2007，27(27):77 －82.

[6]高剑，黄守道，马晓枫，等.基于交互式MRAS策略的无轴承异步电机无速度传感器矢量控制系统[J].电工技术学报，2008，23(11):41－45.GAO Jian，HUANG Shoudao，MA Xiaofeng，et al.Speed sensorless vector control system of bearingless induction motors based on mutual MRAS scheme[J].Transactions of China Electrotechnical Society，2008，23(11):41－45.

[7]孙晓东，朱熀秋，张涛，等.无轴承永磁同步电机径向悬浮力动态解耦控制[J].电机与控制学报，2011，15(11):21 －26.SUN Xiaodong，ZHU Huangqiu，ZHANG Tao，et al.Dynamic de-coupling control of radial suspension forces on bearingless permanent magnet-type synchronous motors[J].Electric Machines and Control，2011，15(11):21 －26.

[8]卜文绍，王少杰，黄声华.三相无轴承异步电机的解耦控制系统[J].电机与控制学报，2011，15(12):32 －37，43.BU Wenshao，WANG Shaojie，HUANG Shenghua.Decoupling control system of three-phase bearingless induction motor[J].E-lectric Machines and Control，2011，15(12):32 －37，43.

[9]张宏荃，张杭，裴军.应用电流模型的无轴承异步电机悬浮控制[J].电机与控制学报，2010，14(3):73－76.ZHANG Hongquan，ZHANG Hang，PEI Jun.Suspension control of bearingless induction motors based on current model[J].Electric Machines and Control，2010，14(3):73 －76.

[10]卜文绍，袁澜，肖隽亚，等.无轴承异步电机的感应补偿控制研究[J].电气传动，2012，43(3):11－14.BU Wenshao，YUAN Lan，XIAO Juanya，et al.Research on induction compensation control of bearingless induction motor [J].Electric Drive，2012，43(3):11 －14.

[11]KARUTZ P，NUSSBAUM T，GRUBER W，et al.Novel magnetically levitated two-level motor[J].IEEE/ASME Transactions on Mechatronics，2008，13(6):658－668.

[12]HIROMI T，KATOU T，CHIBA A，et al.A novel magnetic suspension-force compensation in bearingless induction motor drive with squirrel-cage rotor [J].IEEE Transactions on Industry Applications，2007，43(1):66－76.

[13]MIYAMOTO N，ENOMOTO T，AMADA M，et al.Suspension characteristics measurement of a bearingless motor[J].IEEE Transactions on Magnetics，2009，45(.6):2795 －2798.

[14]SUGIMOTO H，KAMIYA K，NAKAMURA R，et al.Design and basic characteristics of multi-consequent-pole bearingless motor with bi-tooth main poles [J].IEEE Transactions on Magnetics，2009，45(6):2791－2794.

[15]ASAMA J，AMADA M，TAKEMOTO M，et al.Voltage characteristics of a consequent-pole bearingless PM motor with concentrated windings[J].IEEE Transactions on Magnetics，2009，45(6):2823－2826.

[16]LIU Xianxing，WANG Weiran.SVM-DTC control of the bearingless induction motor[C]//International Conference on Measuring Technology and Mechatronics Automation，2010:706－709.

[17]CHIBA A，FUKAO T，RAHMAN M A.Vibration suppression of a flexible shaft with a simplified bearingless induction motor drive[J].IEEE Transactions on Industry Applications，2008，44(3):745－752.

[18]CHIBA A，AKAMATSU D，FUKAO T，RAHMAN M A.An improved rotor resistance identification method for magnetic field regulation in bearingless induction motor drives[J].IEEE Transactions on Industrial Electronics，2008，55(2):852 －860.