SIMULINK中PMSM模型的改进及在参数辨识中的应用

王莉娜，杨宗军

(北京航空航天大学 自动化科学与电气工程学院，北京100191)

0 引言

近年来，随着电力电子技术和稀土永磁材料的快速发展，永磁同步电机(permanent magnet synchronous motor，PMSM)日益受到关注。它在结构上采用高能永磁体作为转子，具有体积小、无励磁损耗、功率密度高等优点，广泛应用于作动系统、数控机床和机器人系统中[1－2]。永磁同步电机的优良性能受到众多学者的关注，对于其在Matlab中的仿真研究也日益增多。

目前，对于永磁同步电机的建模和仿真，得利于MatlabSIMULINK库中有封装好的PMSM模块，可以直接调用，大多集中在控制算法上，而对 PMSM本体的研究甚少。但是，随着应用的日益广泛，系统集成的PMSM模块出现不足，不能满足仿真要求，如电机参数不可在线修改，坐标定义不符合常规逻辑等，给研究带来不便。如何改进PMSM模块，使其适用于变参数变结构的动态仿真，具有实际意义。

本文首先分析指出SIMULINK中集成PMSM模块的不足，然后在建立PMSM数学模型的基础上给出两种改进方法，并进行可行性验证，最后结合自定义PMSM模型，将其应用在电机参数辨识中。

1 SIMULINK中集成PMSM的不足

1.1 电机参数不可在线动态修改

永磁同步电机种类繁多，参数变化大，对于一些特殊的电机仿真，需要在线动态修改电机参数。常规的SIMULINK模块在设定参数时，一般是在仿真开始前通过双击模块后弹出静态对话框进行设置。但是，在对时变系统进行动态仿真，研究变参数变结构模型的时候，模块的参数需要根据仿真环境的要求进行动态变化，这是无法通过设置静态框实现的。

例如在对PMSM的定子绕组电阻值做辨识研究时[3]，需要在线动态修改电阻值以模拟其随温度连续变化的情况，属于变参数仿真。由于系统集成的PMSM模块不支持在线参数修改，使得仿真中只能验证算法对静态量的辨识效果，而对变化量难以考察。考虑从PMSM本体出发，建立适用性更广的电机模型显得必要和有效。

1.2 坐标变换与常规逻辑不同

SIMULINK中集成PMSM模块定义的坐标变换角与国内常规定义不同[4]，如图1所示。常规定义中θ为d轴与α轴的夹角，而SIMULINK中则定义成q轴与α轴的夹角，记为图中的 γ，显然，θ=γ－90°，这导致了在常规的调速系统中反馈回路需要对θ做一次变换。

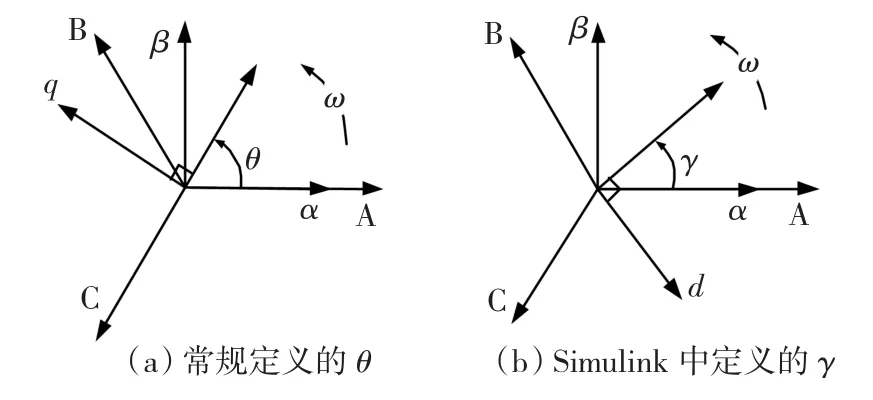
图1 PMSM模型中夹角定义的比较Fig.1 Contrast of defined angles in PMSM model

电机内部采用磁链不变的线性变换，常规从ABC到dq0坐标系的变换矩阵[1]为

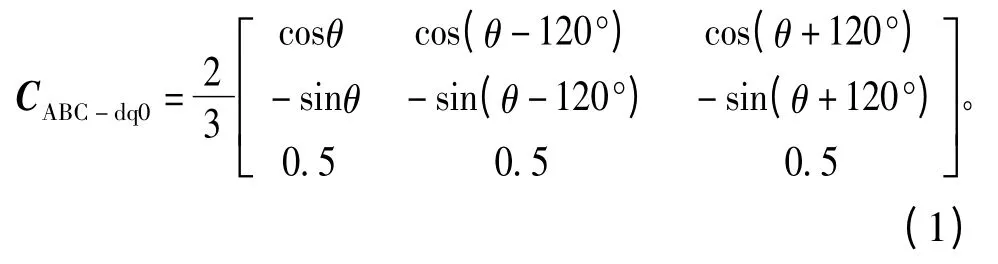
由于坐标定义的差异，集成PMSM模块内部的变换矩阵实际为

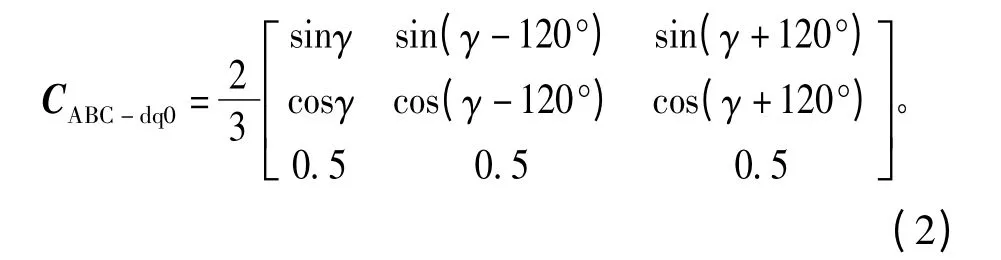
相位角的差异对Clarke变换不影响，但是Park正逆变换会发生改变，使得变换的中间量也有所不同，给分析研究带来不便。

2 对PMSM模型的改进

基于对SIMULINK中集成PMSM模块不足的分析，本文给出两种改进方法，并做对比和讨论。

2.1 方法一:修改库文件模型

为改进原有PMSM模型，使其具有在线动态修改参数的功能，一个直接的方法是根据需要对库文件模型做修改，再重新封装。

打开SimPowerSystems工具箱集成的PMSM仿真模块，鼠标右击并选择“Look Under Mask”命令，将出现其内部结构。模型中包含4个block块，主要的两个为 Electrical model和 Mechanical model。由于系统封装过的PMSM组件处于锁定状态，不允许用户对其直接修改，只能修改库文件。一般的操作为:

1)解锁。选中模块右击，在Link options中选择Go to Library block，然后在打开的库模型中选择Edit/unlock library完成解锁;

2)修改。找到需要修改的模块，替换成信号端、Fcn函数等;

3)更新。返回仿真界面，点击菜单Edit/Update diagram，更新修改的库模型到仿真中。

图2给出了引出转动惯量J前后的PMSM封装对比。仿真时J引脚可接上常量，变量，以及用SFunction写的含参变量的任意信号，实现参数动态变化。

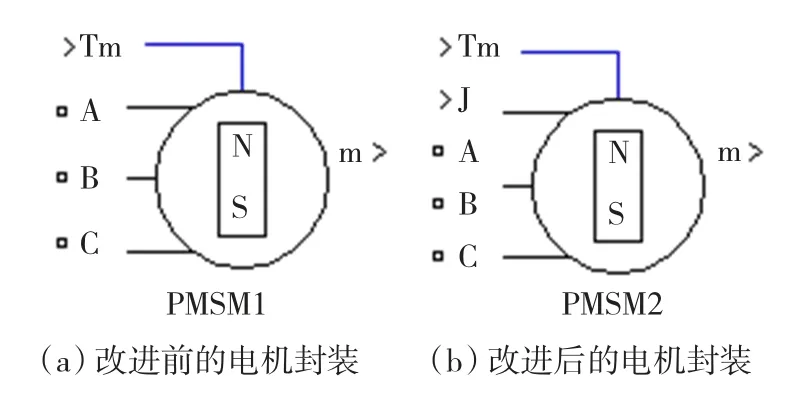
图2 改进前后PMSM模型的封装对比Fig.2 Contrast of PMSM encapsulation before and after improvement

该法是对原 PMSM模型的重新封装，方便快捷，适用于其他任何参数。不过，由于对库文件做了改动，当仿真文件移动到别的环境下时，需将库文件一起拷贝，降低了移植性。

2.2 方法二:创建自定义PMSM模型

方法二是在PMSM数学模型的基础上创建自定义电机模型，适用性广泛。

2.2.1 永磁同步电机的数学模型

为便于分析，假设磁路不饱和，在空间磁场呈正弦分布，不计磁滞和涡流损耗[1]，在定、转子参考坐标系下，PMSM的模型如图3。

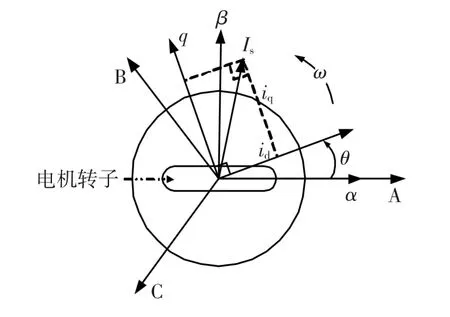
图3 PMSM的物理模型Fig.3 Physical model of PMSM

图中给出了分析同步电机数学模型常用的坐标系，在d－q轴系下PMSM的电压和磁链方程为

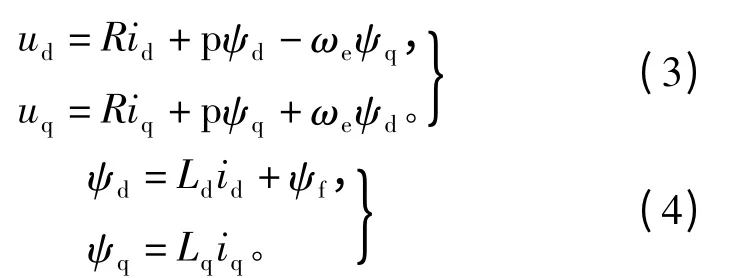
式中:ud、uq分别为 d、q 轴电压;id、iq为 d、q 轴电流;Ld、Lq为 d、q 轴电感;ψd、ψq为 d、q 轴磁链;ψf为永磁体磁链;R为定子绕组电阻;p为微分算子。联立式(3)、式(4)，得

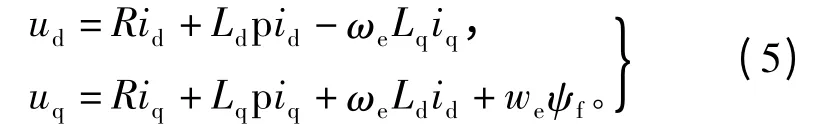
将上式(5)改写成以电流为状态变量的矩阵形式，即

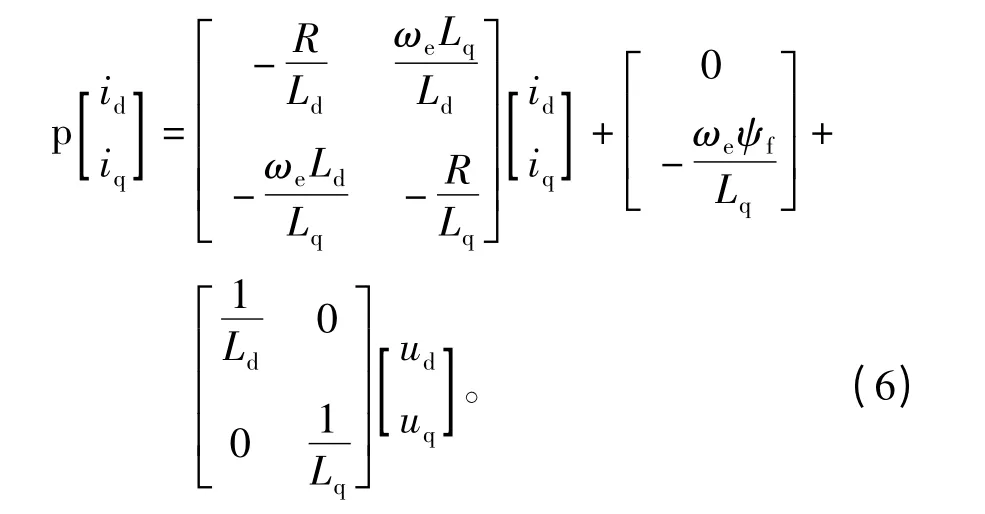
根据状态方程(6)即可在SIMULINK中建立模型，或用S－Function编写关系式。其中变参L、R等均可根据需要，用接线端引出。

在d－q坐标系下PMSM的转矩方程为

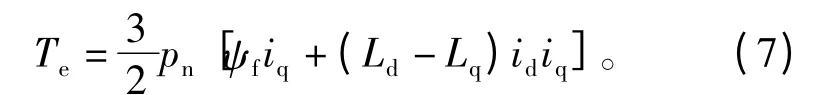
机械运动方程为

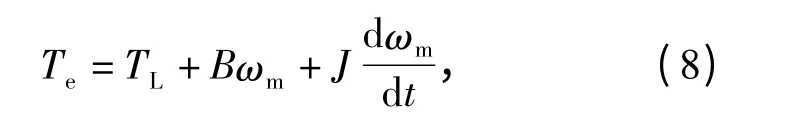
式中:Te为电磁转矩;TL为负载转矩;pn为电机极对数;J为转动惯量;ωm为机械角速度;B为粘滞系数。图4给出了引出J的机械方程模型。

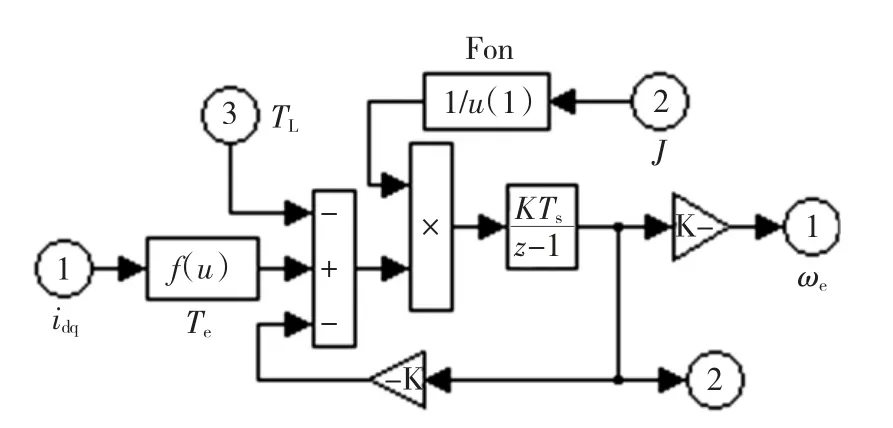
图4 机械运动方程的模型Fig.4 Model of mechanical motion equation

2.2.2 PMSM内部坐标变换

在电机内部，采用磁链不变的线性变换，根据常规变换矩阵(1)，忽略0轴分量，有

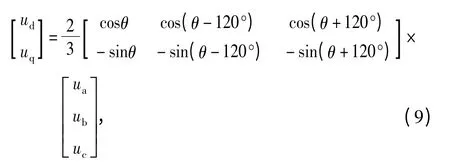
式中θ为d轴与α轴的夹角。

由于自定义的PMSM模型属于信号模型，省去了功率部分，故可由正弦信号直接驱动，配合适当的信号增益可表示功率大小。当控制信号采用SPWM算法时，调制函数为正弦波，可以直接驱动电机模型。对于SVPWM算法，相电压的调制信号是马鞍形波[5]，不可直接引入电机模型，由于其线电压调制函数是正弦波，故可利用线电压信号驱动自定义模型，此时坐标变换需改写成

对应的电流矢量逆变换矩阵在忽略0轴分量时为

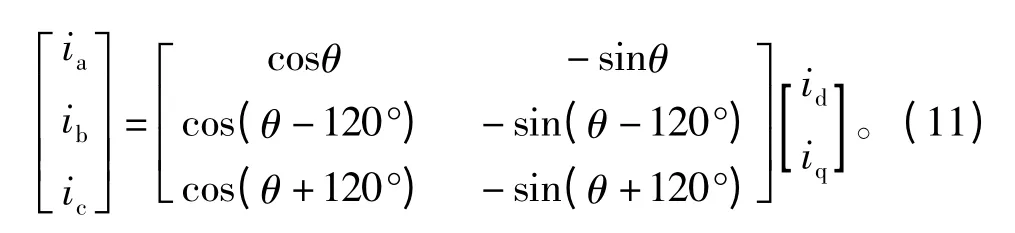
对于SPWM，其线电压的调制函数也是正弦波，故模型可通用。

2.2.3 封装自定义PMSM模型

图5给出了封装好的PMSM模块图，在实际仿真环境中接上输入信号和反馈信号，即可完成相应的PMSM仿真。

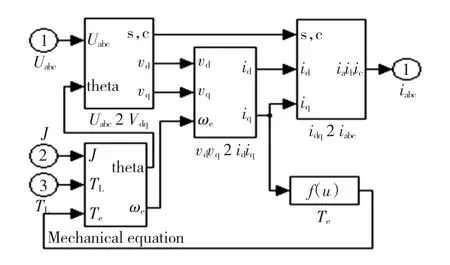
图5 封装的自定义PMSM模型Fig.5 Model of custom PMSM after encapsulates

自定义PMSM模型具有以下特点:

1)参数定义符合国内习惯。模型采用常规逻辑搭建，在考察中间变量时不会出现混乱，而且外部反馈的θ可直接引入，无需变换;

2)适用变参数仿真。自定义PMSM模型的所有参量均可引出，支持在线修改，对变参数变结构模型的动态仿真研究具有实用性;

3)简化系统外围电路。建立调速系统仿真时，自定义PMSM属于信号模型，可由控制信号直接驱动，省去功率开关模块;而且反馈回路可直接引用中间量id、iq，省去坐标反变换。

4)兼容性好。该模型在与其他库模型连接时，可以将电机模块作为信号模型处理，适用于常规连接方法。同时该模型较方法一来说可移植到任何仿真环境中使用。

3 仿真验证

在SIMULINK仿真环境中，建立 SVPWM双闭环调速系统模型[6－9]。通过对集成PMSM模型和改进的两种PMSM模型的对比实验，验证改进模型的正确性。

调速系统中电流调节器采用传统PI设计[7]，其PI参数分别为kp=1 100，ki=7;速度调节器在对比了文献[7－9]后，采用简化的非线性 PI算法，具体设计为

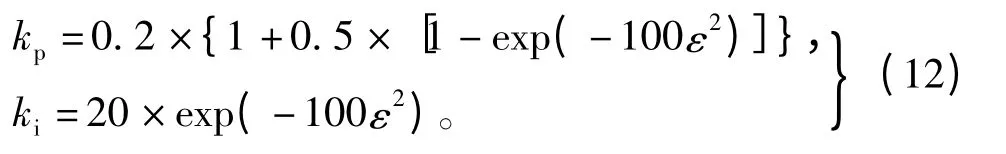
式中ε为速度的误差率

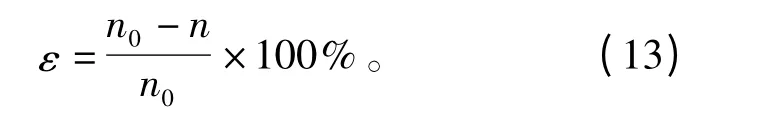
仿真中的电机采用东莞电机有限公司GT17－75S72R型电机参数，其中额定转速N=1 500 r/min，额定转矩T=75 N·m，额定电流I=23 A，绕组电感L=2.1 mH，定子电阻Rs=0.331 Ω，永磁体磁链Ψ=0.353 7 Wb，转子转动惯量 J=0.025 2 kg·m2。

仿真进行0～1 500 r/min的转速阶跃响应实验，结果如图6所示。图6(a)、图6(b)、图6(c)分别对应系统集成PMSM模型，修改库文件模型和自定义PMSM模型的速度响应波形。从图中可以看出，在相同仿真环境下，3种模型得出的结果相同。

图6 不同PMSM模型的速度响应对比Fig.6 Contrast of speed response by different PMSM models

同样，在1 500 r/min恒转速下，对3种模型进行0～75 N·m的转矩阶跃响应对比实验，图7给出了三相电流的响应波形。这里为便于分析和对比，避免引入非线性，PI调节器未加限幅设置。分析波形可见，在仿真环境相同的条件下，3种模型得出的结果一致。仿真证实了改进模型的正确性。

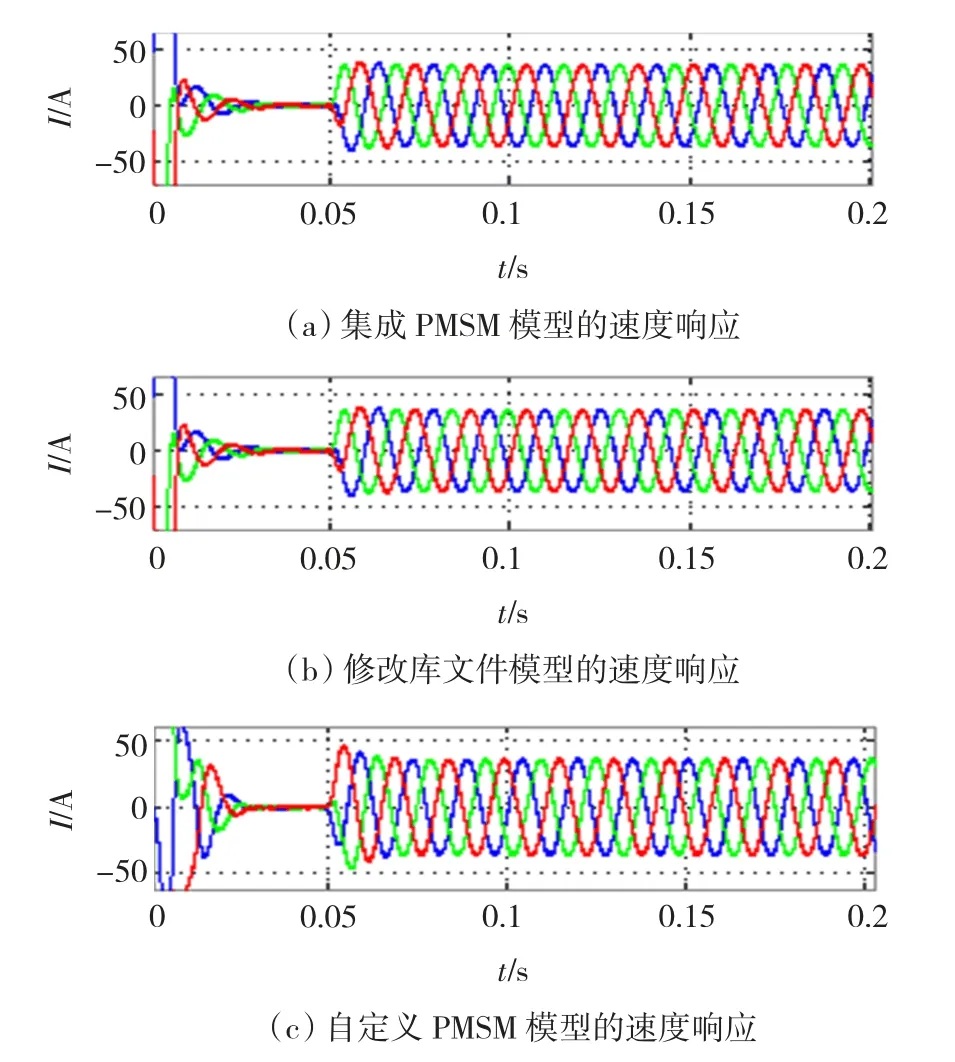
图7 不同PMSM模型的电流波形对比Fig.7 Contrast of current response by different PMSM models

4 参数辨识的应用

在电机常规参数[10－11]和非线性参数[12－14]的辨识算法仿真中，由于模型的局限性往往只能研究静态参数的辨识，而实际中很多参数是变化的，对算法动态性能的验证，就需要模型支持参数的在线动态修改。

文献[6]给出了模型参考自适应辨识算法(model reference adaptive identification，MRAI)在电机转动惯量J识别上的应用，这里结合 MRAI，利用本文改进后的PMSM模型，实现静态和动态J的参数辨识。

图8为MRAI的结构框图，其对应参考模型为

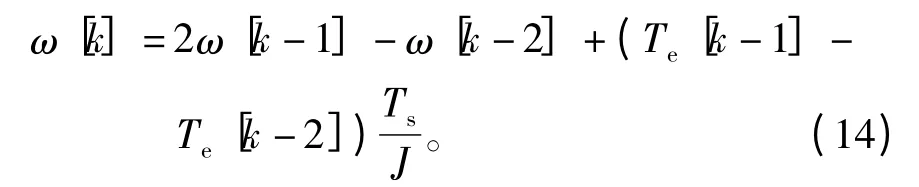
可调模型为

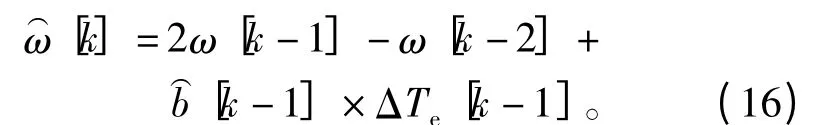
使用Landau离散时间递推参数辨识机制，自适应机制为

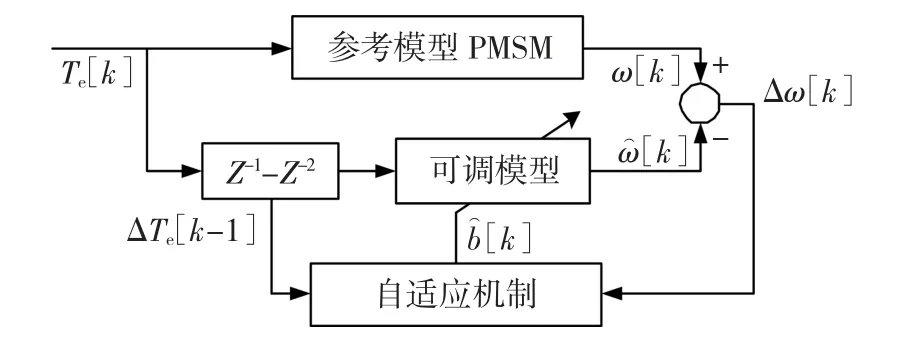
图8 MRAI的结构框图Fig.8 The structure of MRAI

依据MRAI的参数关系，在 SIMULINK中建立辨识模型。图9为带有辨识模块的自定义PMSM矢量控制框图。

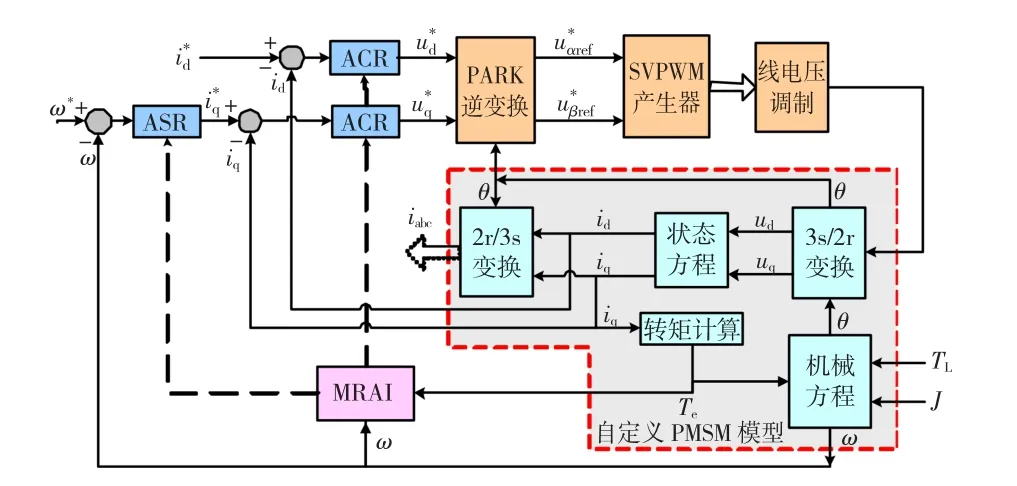
图9 矢量控制框图Fig.9 The vector control diagram

转子转动惯量 J0=0.025 2 kg·m2，给定 J为J0、2J0、5J0、10J0的连续阶跃信号，β 为 0.05，辨识参数J自收敛，未设置初值，其它参数同第三节给出，结果如图10所示。分析波形可见，在仿真时间t=0.1 s，0.15 s，0.2 s 时刻，转动惯量发生跳变，而辨识的J均在0.005 s内跟踪并准确识别。

图10 阶跃转动惯量的辨识结果Fig.10 Identification results of step inertia

当给定信号按照J=[2+sin(20πt)]J0正弦规律变化时，响应波形如图11所示，辨识值可以很快跟踪上给定值，与上述结论相同。仿真结果证实，改进后的PMSM可实现参数的在线动态修改，并在参数辨识中很好的运用。

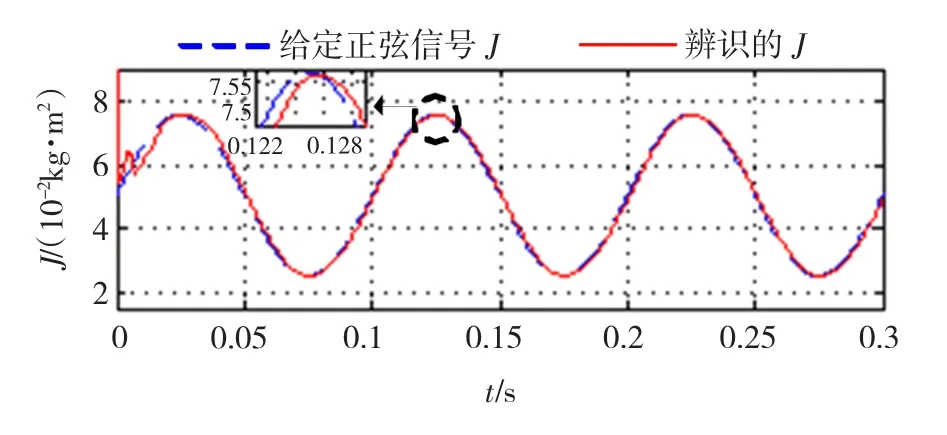
图11 正弦转动惯量的辨识结果Fig.11 Identification results of sine inertia

该PMSM模块适用于变参数仿真，对于电机其他参数的辨识也同样适用，这里不予展开说明，仅以J为例验证模型的适用性。

5 结语

SIMULINK中集成的永磁同步电机模型在仿真中应用广泛，但存在不足:电机参数不可在线动态修改，局限了模型在变参数动态仿真中的应用;坐标定义不符合常规逻辑，给中间量的分析和反馈信号的处理带来不便。本文针对不足，提出了对PMSM模型的两种改进方法，通过修改库文件模型和自定义PMSM模型弥补了系统集成模型的不足。仿真验证了改进模型的正确性，并结合MRAI算法将其运用在电机变参数辨识中，拓展了PMSM仿真的应用范围。改进的PMSM模型在时变系统变参数变结构模型的动态仿真中具有较大的实用性。

[1]李崇坚.交流同步电机调速系统[M].北京:科学出版社，2006:12 －54，263 －287.

[2]DE ALMEIDA A T，FERREIRA F J T E，FONG J A C.Standards for efficiency of electric motors [J].IEEE Industry Applications Magazine，2011，17(1):12－19.

[3]WILSON S D，STEWART P，TAYLOR B P.Methods of resistance estimation in permanent magnet synchronous motors for realtime thermal management[J].IEEE Transactions on Energy Conversion，2010，25(3):698－707.

[4]刘金海.Simulink自带永磁同步电动机模型矢量坐标变换分析与国产化改造[J].漳州师范学院学报:自然科学版，2010，23(4)4:73－76.LIU Jinhai.Vector coordinate transformation analysis and domestic reform of Simulink PMSM model[J].Journal of Zhangzhou Normal University:Natural Science，2010，23(4):73 －76.

[5]陆海峰，瞿文龙，张磊，等.基于调制函数的 SVPWM算法[J].电工技术学报，2008，23(2):37 －43.LU Haifeng，QU Wenlong，ZHANG Lei，et al.SVPWM algorithm based on modulation functions[J].Transactions of China Electrotechnical Society，2008，23(2):37 －43.

[6]XU Huazhong，XIE Jun.A vector-control system based on the improved MRAS for PMSM[C]//Intelligent Systems and Applications，2009:1 －5.

[7]LI Yun，KIAM H A，CHONG G C Y.PID control system analysis and design[J].IEEE Control Systems，2006，26(1):32 －41.

[8]王江，王静，费向阳.永磁同步电动机的非线性 PI速度控制[J].中国电机工程学报，2005，25(7)，125 －130.WANG Jiang，WANG Jing，FEI Xiangyang.Nonlinear PI speed control of permanent magnetic synchronous motor[J].Proceedings of the CSEE，2005，25(7):125 －130.

[9]SANT A V，RAJAGOPAL K R.PM synchronous motor speed control using hybrid fuzzy-PI with novel switching functions[J].IEEE Transactions on Magnetics，2009，45(10):4672 －4675.

[10]LI Shihua，LIU Zhigang.Adaptive speed control for permanentmagnet synchronous motor system with variations of load inertia[J].IEEE Transactions on Industrial Electronics，2009，56(8):3050－3059.

[11]王庆龙，张崇巍，张兴.基于变结构模型参考自适应系统的永磁同步电机转速辨识[J].中国电机工程学报，2008，28(9)，71－75.WANG Qinglong，ZHANG Chongwei，ZHANG Xing.Variablestructure MRAS speed identification for permanent magnet synchronous motor[J].Proceedings of the CSEE，2008，28(9):71 －75.

[12]LUUKKO J，PYRHONEN J.Selection of the parameters of a permanent magnet synchronous machine by using nonlinear optimization[J].IET Electric Power Applications，2007，1(2):255－263.

[13]金海，黄进.基于模型参考方法的感应电机磁链的自适应观测及参数辨识[J].电工技术学报，2006，21(1):65 －69.JIN Hai，HUANG Jin.Adaptive flux estimation and parameters identification of induction motors based on model reference approach[J].Transactions of China Electrotechnical Society，2006，21(1):65－69.

[14]UNDERWOOD S J，HUSAIN I.Online parameter estimation and adaptive control of permanent-magnet synchronous machines[J].IEEE Transactions on Industrial Electronics，2010，57(7):2435－2443.