纯电动汽车充电机输出阻抗特性

李晶，姜久春

(北京交通大学 电气工程学院，北京100044)

0 引言

充电系统为纯电动汽车运行提供能量补给，是纯电动汽车重要基础支撑系统，也是电动汽车商业化、产业化过程中的重要环节[1]。纯电动汽车充电系统由充电机和大容量动力电池组成。在充电过程中，充电机与动力电池组成级联系统，随着外部环境和充电需求的变化，充电机的输出阻抗特性随之发生变化，由于充电机与电池之间的相互作用，导致充电系动态响应变差，甚至失去稳定性，不能进行正常充电，对电池造成损伤，严重的影响充电安全。Middlebrook提出的级联系统阻抗比匹配原则被广泛应用于分布式供电系统中，但对于纯电动汽车充电机的设计往往忽略充电机与电池组成了级联系统，并且不对其输出阻抗进行约束。

本文首先建立充电机动态小信号模型，然后分析充电机输出阻抗与直流工作点，输出滤波器等效串联电阻及控制环路特性的关系。最后对应用于纯电动环卫车的车载充电机进行测试，对理论分析进行验证。为约束纯电动汽车充电机输出阻抗提供依据。

1 理论分析

典型的纯电动汽车充电机与电池组成的系统结构如图1所示。充电机的输出阻抗定义为 Zout，电动汽车用动力电池的输入阻抗定义为Zin，充电机能够稳定运行的条件是，Zout与Zin的比值满足乃奎斯特稳定性判据[2－3]。由于动力电池受到生产工艺的制约，其输入阻抗不容易被调整。所以一般通过调整充电机的输出阻抗来调整阻抗比以达到稳定运行的目的。

图1 纯电动汽车充电机系统结构Fig.1 BEV charger system architecture

1.1 阻抗特性与稳定性的关系

Middlebrook于1976年提出了判断级联系统稳定性的阻抗比判据。如图1所示，Zout和 Zin是两个级联模块在连接端口处的输出阻抗和输入阻抗。Middlebrook的阻抗比判据是最早也是应用最广泛的判断级联系统是否稳定的方法。其原理如式(1)～式(3)所示，其中 G1，G2为两个子系统的电压增益之积，阻抗比Zout/Zin可以看做系统的环路增益。根据奈奎斯特稳定性判据，为了保证系统的稳定性，Zout/Zin的Nyquist曲线不能进入或包围(－1，0)点，如图2所示。因此，Zout/Zin被称为最小环路增益。为了保证系统具有一定的相位和增益裕量，最小环路增益的Nyquist曲线必须满足一定的条件，如式(3)所示。它要求在全频率范围内前级模块的输出阻抗小于后级模块的输入阻抗。如果级联系统满足这个条件，不但级联后系统的稳定性可以保证，并且级联系统的两个部分可以解耦[2，4]。

图2 阻抗判据示意图Fig.2 Impedance criterion

其中:

1.2 纯电动汽车充电机模型

本文以全桥拓扑构成的充电机为例建立其动态小信号模型并分析它的输出阻抗特性。

图3 充电机闭环小信号模型Fig.3 Closed-loop small signal model of BEV charger

纯电动汽车充电机等效动态小信号模型如图3所示，其中n为变压器变比，Lf，Cf分别为输出滤波器电感和电容，RC，RL分别为输出滤波电容和电感的等效串联电阻，H(s)为输出电压采样网络传递函数，Gc(s)为补偿网络传递函数，Fm(s)为PWM调制器增益。由图3可见输入电压扰动，输出滤波器等效串联电阻变化都会导致由小信号模型获得的表征充电机特征传递函数的变化。由该小信号模型可推导出充电机开环输出阻抗Zop如式(4)所示，闭环输出阻抗Zoc如式(5)所示，其中T(s)为充电机环路增益如式(6)所示，Gvd为控制到输出传递函数如式(7)所示。典型的充电机开环与闭环输出阻抗Bode图如图4所示。开环时，在低频段输出阻抗与输出滤波电感等效串联电阻RL相关，高频段与输出滤波电容等效串联电阻RC相关，在输出滤波器谐振频率处开环输出阻抗达到最大值。引入闭环后，在低频段和中频段输出阻抗幅值比开环时减少了很多，在输出滤波器谐振峰值处输出阻抗极值得到了很好的抑制，但在超过截止频率后的频段内，闭环输出阻抗呈现开环输出阻抗特性，不在受控制环路影响[5－6]。

图4 输出阻抗开环与闭环伯德图Fig.4 Closed-loop and open-loop output impedance

其中:

1.3 大功率动力电池的阻抗特性

蓄电池是化学能与电能相互转换的电源装置，其工作过程就是化学反应过程。蓄电池内阻的主体为电解液，它并无感抗，而且在工频下其容抗也可以忽略，因此理论上可以用电阻模型等效蓄电池。而实际运行中，蓄电池常常处于“交流”状态下。尤其在使用PWM型充电机对其充电时，其充电电流和电压不是单纯直流而是含有多种谐波成分的交流纹波电压和电流与直流电压和电流的叠加，因此大功率动力电池的模型不能等效为单纯的电阻，而是含有电阻，电容，电感的阻抗模型，如图5所示，图中R为电解液和隔板产生的欧姆电阻，L为引线电感，Ro为电化学极化电阻(电荷转移电阻)。W(Warburg阻抗)为浓差极化阻抗，C为极板双电层电容[7]。因此电池的阻抗特性会随频率的变化而变化。图6所示为实际测得的纯电动汽车用动力电池阻抗特性图。从图中可以看到，电池阻抗的幅值和相位是频率的函数，并且会出现极小值。

图5 电池阻抗模型Fig.5 Impedance model of battery

图6 电池阻抗特性Fig.6 Battery impedance characteristics

2 影响闭环输出阻抗特性的因素

为了更深入的了解纯电动汽车充电机输出阻抗特性，以便于在设计过程中根据电池阻抗特性制定充电机输出阻抗标准，根据前文所述充电机小信号模型，从直流工作点，输出滤波器参数，控制环路特性3个主要因素对充电机输出阻抗特性的影响进行仿真分析，以便于充电机的设计与优化。本文基于实际应用于纯电动环卫车车载充电机的参数进行分析，参数如下:Vin=385～395 V，Vout=450 V，Pout=0～3 500 W。

2.1 直流工作点对闭环输出阻抗的影响

对于纯电动汽车充电机，在主电路拓扑和电路参数均以确定的情况下，充电机运行的直流工作点随电网环境和工作状态的变化而变化。主要变化有，由于电网电压波动引起的输入电压变化和由于电池充电需求不同引起的充电电流变化。为了使在输入电压和充电电流可能变化范围内，输出阻抗变化不会影响充电系统稳定性，有必要研究输出阻抗随工作点变化的规律。

图7所示为充电机输出阻抗随工作点变化的频率特性图。充电机在工作过程中，大部分时间运行在恒流充电状态，图7(a)为充电机闭环输出阻抗随充电电流变化的波特图，可见在充电电流变化的过程中，其闭环输出阻抗特性基本没有发生变化。由图7(b)可见，在考虑了电网电压波动后，充电机设计直流母线电压变化范围是385～395 V，在这个变化范围内充电机的闭环输出阻抗几乎没有变化，只是在谐振频率处阻抗峰值略有不同。

图7 闭环输出阻抗与直流工作点的关系Fig.7 Closed-loop output impedance Vs.DC operating point

2.2 输出滤波器参数对闭环输出阻抗的影响

为了降低输出电压和电流的纹波，输出噪声以及输出负载发生变化时引起输出电压的变化，功率电感和大容量电解电容常被用于纯电动汽车充电机的输出滤波器中。电容和电感的等效模型如式(12)和式(13)所示。电容的串联等效电阻会产生一个高频零点如式(10)所示，电感的串联等效电阻会产生一个低频零点如式(11)所示。通常同一生产厂家生产的同型号电力电容器其等效串联电阻(equivalent series resistance，ESR)值与电容值的乘积为一常数，在 RCC=65×10－6左右。这意味着电容的ESR产生的高频零点是固定的。例如CDE生产的某一型号的电容查其器件手册可以知道RCC大约为90×10－6，因此可以根据公式(10)计算电容产生的高频零点。

为了研究输出滤波电容器等效串联电阻对闭环输出阻抗的影响，在上述车载充电机模型中，设定输出滤波电容等效串联电阻的变化范围为10～100 mΩ，分析在此变化范围内输出阻抗的变化规律。

图8所示为闭环输出阻抗Zoc随输出滤波电容等效串联电阻RC变化的规律。由图可见，在整个频率范围内，随着输出滤波电容等效串联电阻的增大，闭环输出阻抗随之增大。纯电动汽车充电机实际设计过程中往往会使用多个同型号电容并联的方法增加电容量，达到降低输出电压纹波的目的。多个电容并联后电容量成比例增大的同时输出滤波电容等效串联电阻成比例减小。因此输出阻抗幅值降低，有利于级联后系统的稳定。但输出电容等效串联电阻的降低会降低充电机自身的稳定裕度，在考虑使用多电容并联增大电容量时要折中考虑充电机的稳定性与级联后系统的稳定性。

图8 输出滤波电容等效串联电阻与闭环输出阻抗的关系Fig.8 Closed-loop output impedance Vs.ESR of output filter capacitor

为了研究输出滤波电感等效串联电阻对输出阻抗的影响，在上述车载充电机模型中，设定输出滤波电感等效串联电阻的变化范围为10～100 mΩ，分析在此变化范围内输出阻抗的变化规律。

图9 输出滤波电感等效串联电阻与闭环输出阻抗的关系Fig.9 Closed-loop output impedance Vs.ESR of output filter inductor

图9 所示为闭环输出阻抗Zoc随输出滤波电感等效串联电阻RL变化的规律。由图可见，随着输出滤波电感等效串联电阻的增大，低频段闭环输出阻抗随之增大，中频段和高频段输出滤波电感等效串联电阻对闭环输出阻抗基本没有影响。由式(4)可知输出滤波电感等效串联电阻为系统引入了一个零点，由于一般情况下输出滤波电感等效串联电阻引入的是低频零点，因此只在低频段对系统特性产生影响，进而对低频段的闭环输出阻抗产生影响。在电感的制作中很难精确的控制等效串联电阻的大小，因此在充电机的设计中往往通过控制环路的设计降低电感引入的低频零点对系统的影响。

2.3 控制环路特性对闭环输出阻抗的影响

为了保证在全频率范围内，充电机的输出阻抗小于电池的输入阻抗，控制环路的设计尤为重要。穿越频率fc和相位裕度Pm是控制环路设计的两个重要因素。根据香浓采样定理在开关型电力电子变换器中，穿越频率的选择要低于开关频率的1/2，一般选择为开关频率的1/5～1/4，甚至有时候会选择开关频率的1/20～1/10。相位裕度一般选择大于 45°[8]。

为了研究输出穿越频率对闭环输出阻抗的影响，在上述车载充电机机模型中，设定穿越频率的变化范围为5～15 kHz，分析在此变化范围内闭环输出阻抗的变化规律。

图10所示为闭环输出阻抗随穿越频率变化的规律。由图可见，随着穿越频率的增大，闭环输出阻抗幅值在低频段和中频段明显减小，但在高频率段，输出阻抗的幅值随穿越频率的增加基本没有变化。输出阻抗谐振峰值频率随穿越频率的增加而增加。因此在充电机的设计中提高系统的穿越频率，既可以提高级联后系统的稳定性又可以提高充电机的动态响应速度[9]。

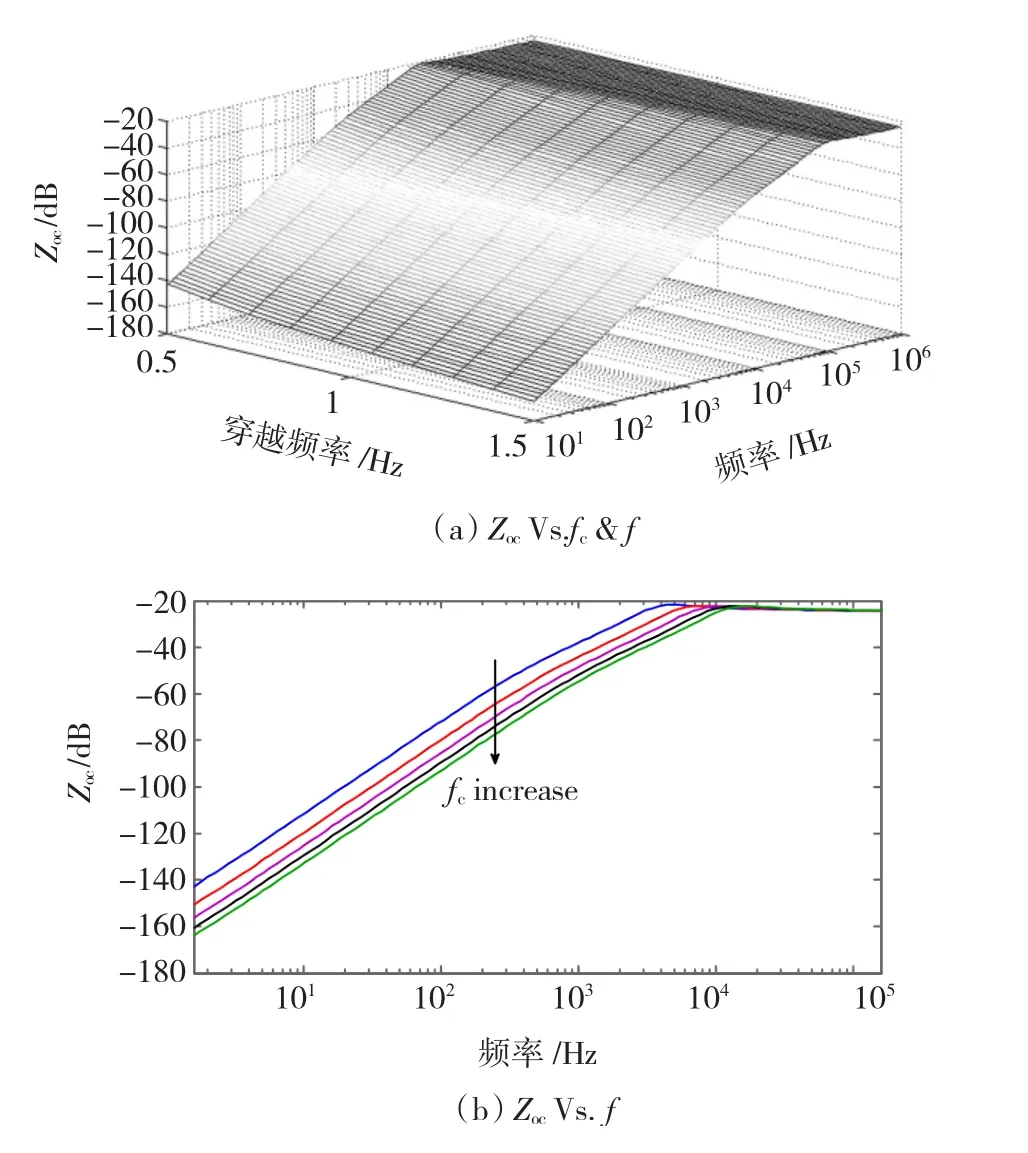
图10 穿越频率与闭环输出阻抗的关系Fig.10 Closed-loop output impedance Vs.crossover frequence

为了研究相位裕度对闭环输出阻抗的影响，在上述车载充电机模型中，设定相位裕度的变化范围为45～75°，分析在此变化范围内输出阻抗的变化规律。

图11所示为闭环输出阻抗随相位裕度的变化规律。由图可见，在低频段随着相位裕度的增大，闭环输出阻抗随之增大，但在较高频率处基本没有变化。输出阻抗峰值随相位裕度的增加而降低。由此可见在充电机设计过程中应该考虑适当的提高相位裕度降低输出阻抗峰值。

图11 相位裕度与闭环输出阻抗的关系Fig.11 Closed-loop output impedance Vs.phase margin

3 实验验证

使用纯电动环卫车用3.5 kW车载充电机测试其闭环输出阻抗随直流工作点，输出滤波器参数，控制环路参数变化的规律。测试输入电压变化范围385～395 V，充电电流变化范围5～30 A。测试结果如图12所示。

图12(a)所示为充电机在设计参数下，闭环输出阻抗的波特图。图12(b)、图12(c)、图12(d)、图12(e)所示分别为当输入电压，充电电流，穿越频率，相位裕度相对于设计参数变化时闭环输出阻抗的波特图。图12(a)，图12(b)对比了不同输入电压下输出阻抗的变化，输出阻抗特性基本没有发生变化;图12(a)，图12(c)对比了不同充电电流下输出阻抗的变化，输出阻抗特性也基本没有发生变化;图12(a)，图12(d)对比了穿越频率变化对输出阻抗的影响，从图中可以明显看出的是输出阻抗的峰值频率随着穿越频率的增大而增大。低频段处输出阻抗，在穿越频率15 kHz时比10 kHz时略有降低;图12(a)，图12(e)对比了相位裕度对输出阻抗的影响，从图中可以明显看出，相位裕度对输出阻抗峰值的影响，相位裕度增大显著降低了输出阻抗峰值。由以上分析可知，测试结果与理论分析基本一致。

图12 实际测量的闭环输出阻抗Fig.12 Measured closed-loop input impedance

4 结论

本文研究了纯电动汽车充电机输出阻抗特性。并用纯电动环卫车用车载充电机进行了验证，得到以下结论:

1)输入电压，充电电流发生变化时，全频率范围内充电机的闭环输出阻抗基本保持不变。

2)输出滤波电容等效串联电阻增大时，全频率范围内充电机闭环输出阻抗随之增大，影响级联后系统的稳定性;输出滤波电感等效串联电阻增大时，低频段充电机的闭环输出阻抗增大，中频段和高频段基本不变。通过设计控制环路可以很好的抑制输出滤波电感对系统稳定性的影响。

3)穿越频率增大时，低频段和中频段充电机的闭环输出阻抗降低，高频段基本保持不变，输出阻抗峰值频率随穿越频率的增加而增加;相位裕度增大时，低频段和中频段充电机的闭环输出阻抗增大，高频段基本保持不变，输出阻抗峰值随相位裕度增加而降低。

[1]章桐，贾永轩.电动汽车技术革命[M].北京:机械工业出版社，2010:142－175.

[2]MIDDLEBROOK R D.Input filter considerations in design and application of switching regulators[C]//Proc IEEE IAS Annual Meeting，1976:336 －382.

[3]XIE G，WANG L.Controllability and stability of switched linearsystems[J].Systems ＆ Control Letters，2003，48:135 －155.

[4]FENG X，LIU J，LEE F C.Impedance specifications for stable DC distributed power systems[J].IEEE Trans Power Electronics，2002，17(2):157 －162.

[5]ERICKSON R W.Fundamentals of power electronics[M].New York:Library of Congress Cataloging in Publication，2001:185－258.

[6]全书海，郝世强，黄亮.燃料电池用大升压比DC/DC器双闭环控制[J].电机与控制学报，2011，15(10):28－35.QUAN Shuhai，HAO Shiqiang，HUANG Liang.Novel doubleclosed-loop control for DC/DC converter with large voltage step-up ratio[J].Electric Machines and Control，2011，15(10):28－35.

[7]黄浩.蓄电池电量技术的研究与实现[D].长沙:湖南大学，2007.

[8]PRESSMAN Abraham I.Switching power supply design[M].New York:McGraw-Hill Companies，1998:355 －384.

[9]LIBERZON D，MORSE A S.Basic problems in stability and design of switched systems [J].IEEE Control Systems Magazine，1999，19(5):5970.