旋挖钻机大三角变幅机构受力分析数学模型的建立

高强，秦爱国，张宽裕，李砚耕

（1、3、4.中国地质大学（武汉），湖北武汉430074；2.玉柴桩工(常州)有限公司，江苏常州213164）

1 前言

旋挖钻机因具有施工速度快、成孔质量好、环境污染小、操作灵活方便、安全性能高及组合功能多等优势，已成为灌注桩施工的主要成孔设备，被广泛应用于高速铁路、高速公路、高层建筑、桥梁等大型工程的桩基础施工。

旋挖钻机变幅机构是桅杆的支撑机构，控制桅杆的起落、倾斜等动作，工作时承受钻具重量、动力头产生的反扭矩及加压油缸产生的反作用力，是钻机的关键部件。变幅机构按结构形式可分为平行四边形式和大三角式，中小型钻机一般采用平行四边形变幅机构，机动灵活；大型钻机（最大输出扭矩大于300kNm）一般采用大三角变幅机构，稳定性好。变幅机构的受力分析是设计的一个难点，国内厂家一般采用经验设计或用理论力学简单地分析一下，往往与实际情况相差甚远。本文用理论力学、弹塑性力学和液体的弹性模量等相关理论与知识，对大三角形变幅机构各铰接点受力进行分析并建立了数学模型，希望能给旋挖钻机设计人员在确定油缸参数及进行结构件设计时提供理论参考，并希望能够起到抛砖引玉的作用，从而提高我国旋挖钻机设计的理论性、规范性与合理性。

2 建立数学模型

动臂、变幅油缸和桅杆油缸是大三角变幅机构的重要部件。之所以重要，是因为它们所受的载荷情况最复杂，受力最大。并且在旋挖钻机提升工况下，桅杆油缸、变幅油缸、动臂所受的载荷最大，所以在数学模型建立的过程中，主要应该建立在提升工况下的铰接点的受力分析数学模型。由于桅杆油缸比较长，并且两桅杆油缸的夹角非常小，所以在分析过程中，将两个桅杆油缸看做平行，由此模型可以由三维状态简化为二维状态。此数学模型的建立需分为三步：

第一步：在提升工况下，对桅杆进行受力分析，画出桅杆的受力图（图1）。

图中：

Fd——桅杆在桅杆油缸铰接点D处所受的拉力

Fax——桅杆在与动臂铰接点A处所受的X方向上的分力

Fay——桅杆在与动臂铰接点A处所受的Y方向上的分力

G1——桅杆总成（含动力头）重量

G2——钻具（含钻渣）重量

Fs——提升卷扬钢丝绳的拉力，在不考虑摩擦、并且假设钢丝绳做匀速直线运动的情况下，Fs=G2

α——Fd与铅垂线的夹角

γ——Fs与铅垂线的夹角

将图1进行简化，画出桅杆的受力示意图（见图2）。

图1

根据理论力学的刚体受力后的平衡条件,在X方向和Y方向列平衡方程

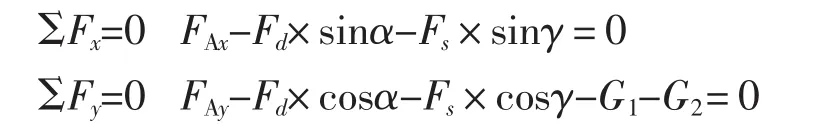
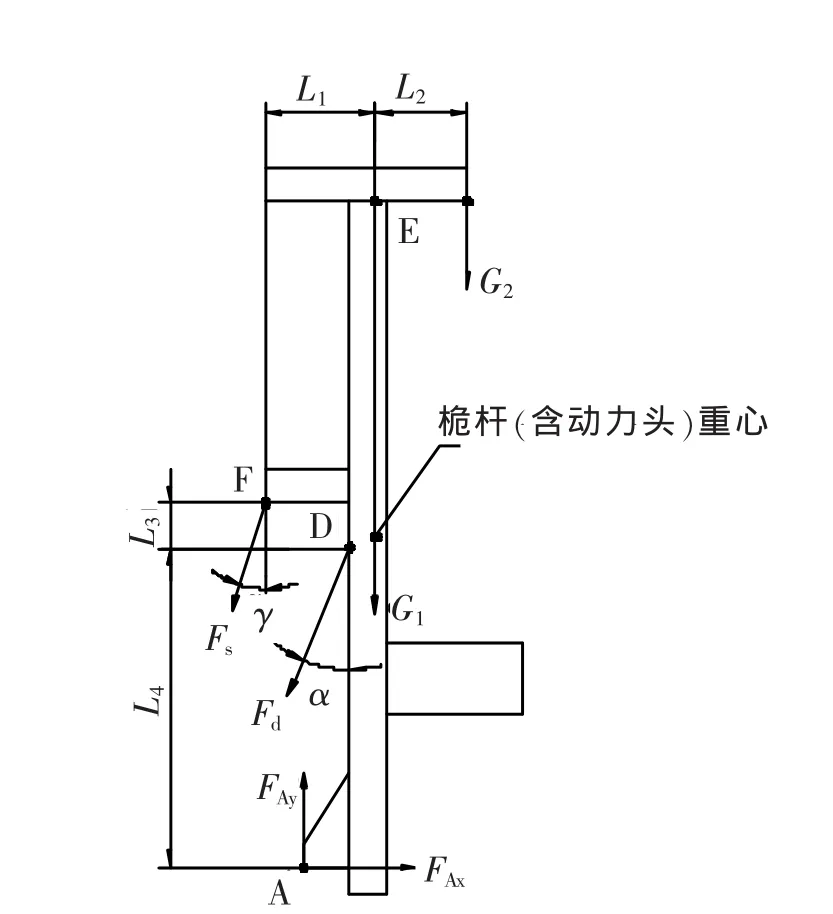
图2

由此可以导出数学模型

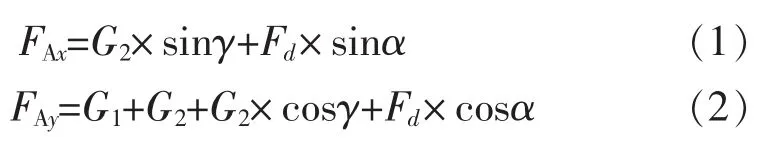
这里Fd需要通过求解变形协调方程来得到。

第二步：列变形协调方程

在理论力学的范畴内，不能解决上述的静不定问题，这时可以利用弹塑性力学理论，列出变形协调方程，与上面的静力学方程联立，才能求得唯一的一组解。

（1）同样以桅杆为研究对象，在图2的受力分析基础上进行简化，将A点简化为固定端，只保留在D点能产生水平方向位移的载荷，即所有弯矩和所有水平方向上的力，如图3所示。

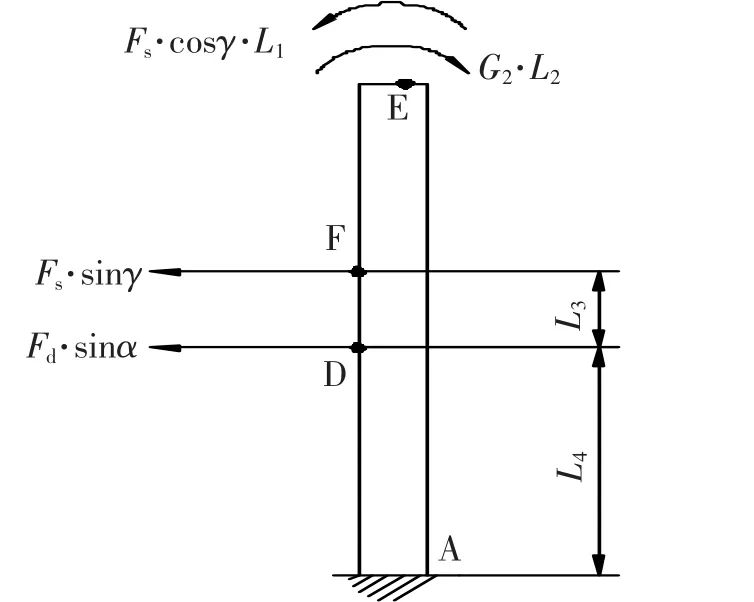
图3

（2）将图3的桅杆从D点截断，保留下面部分，分析D点的受力情况，合并水平方向上的力和所受的弯矩，如图4所示。

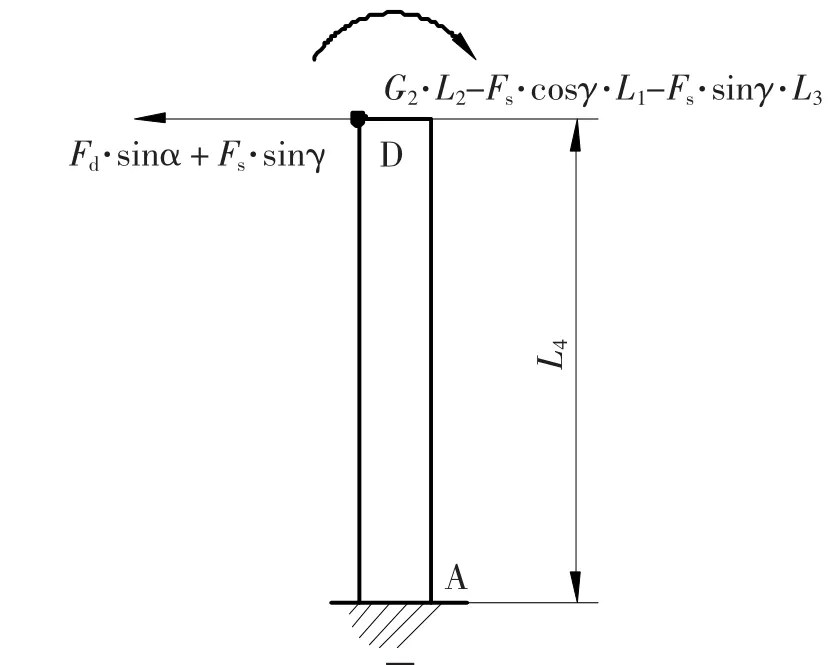
图4

（3）根据弹塑性力学理论，列出D点由于力和扭矩的作用，而产生的在水平方向上的位移WD。

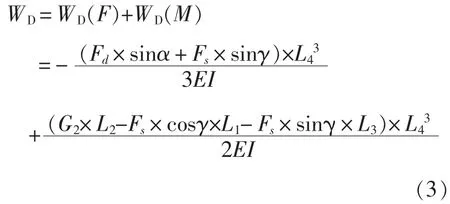
式中E——桅杆的弹性模量

I——桅杆的转动惯矩（4）求桅杆油缸由于提升钻具而产生的压缩量Δl

油缸里的液压油的压缩量,取决于油柱的长度、油缸内径、液压油前后所承受的压力差和液压油的体积弹性模量,具体关系如下

式中h——油缸内被压缩的液压油的原长度

K——液体的体积弹性模量，一般选700～1400MPa

d——液压油缸内径

ΔF——液压油缸活塞杆载荷变化差，值等于Fd－FD

理性决策和策略互动涉及到信息和赋值之间的协调，从而根据偏好进行编码。信息和赋值相互协调，使偏好变成了信念逻辑和博弈。但另一方面自然语言是封闭的，包括对哲学家所关注的“语力”(discourse obligation)的研究。

Fd：在提升工况下，桅杆在桅杆油缸铰接点D处所受的拉力

FD：在非提升工况下，桅杆在桅杆油缸铰接点D处所受的拉力

（5）在铰接点D处列变形协调方程，得出Wo和Δl之间的关系式。

在提升工况下，桅杆受力发生变化，由此带来桅杆油缸活塞杆的轴向位移Δl和桅杆的弯曲变形Wo，具体协调关系见示意图5所示。

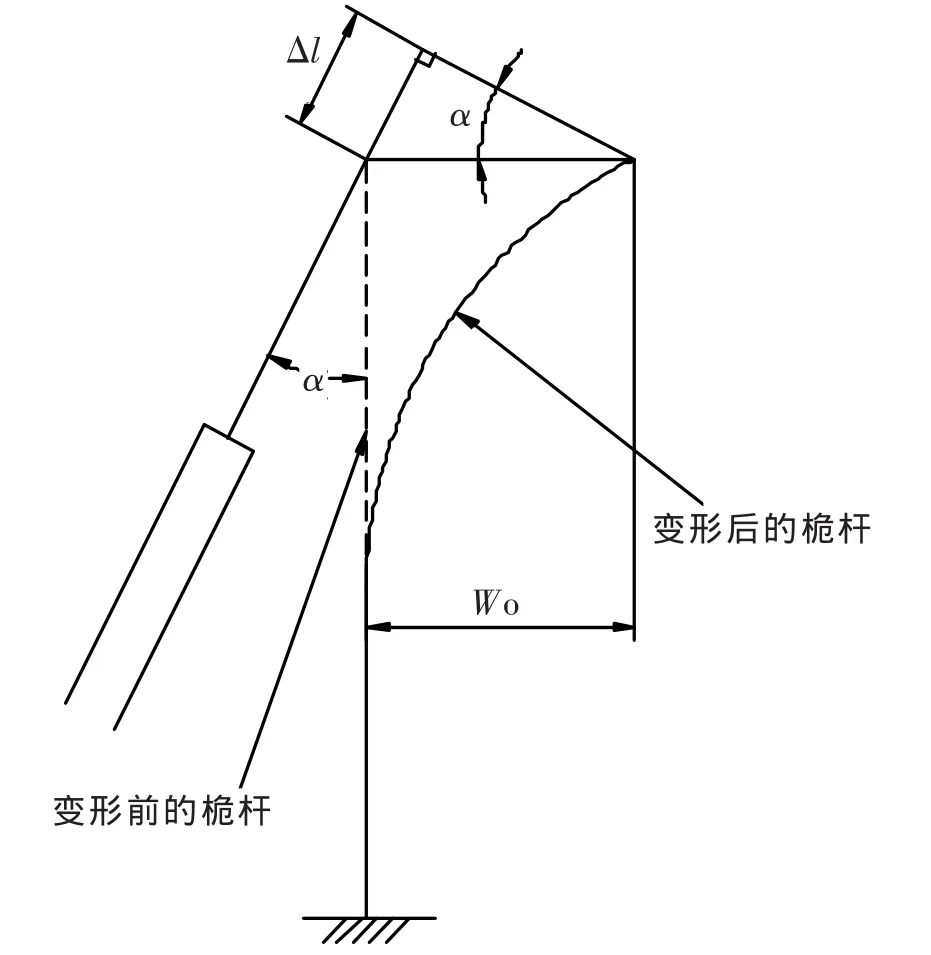
图5

根据图5，列出变形协调方程

联立方程3、4、5所组成的方程组，可以得到方程

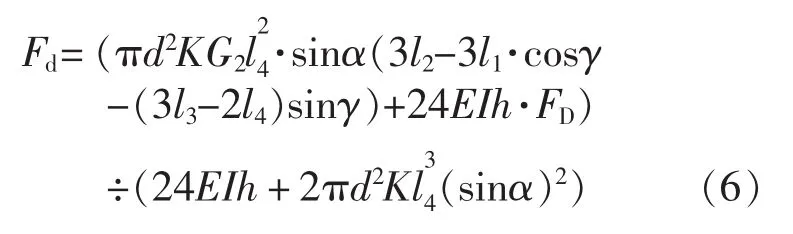
这里FD是未知数，需要在下一步中求得。

以桅杆为研究对象，进行受力分析，如图6所示。此时桅杆共受到三个力的作用，根据刚体的三力平衡汇交原理，画出受力示意图，如图7所示。O点为桅杆重力作用线和桅杆油缸轴线延长线的交点。

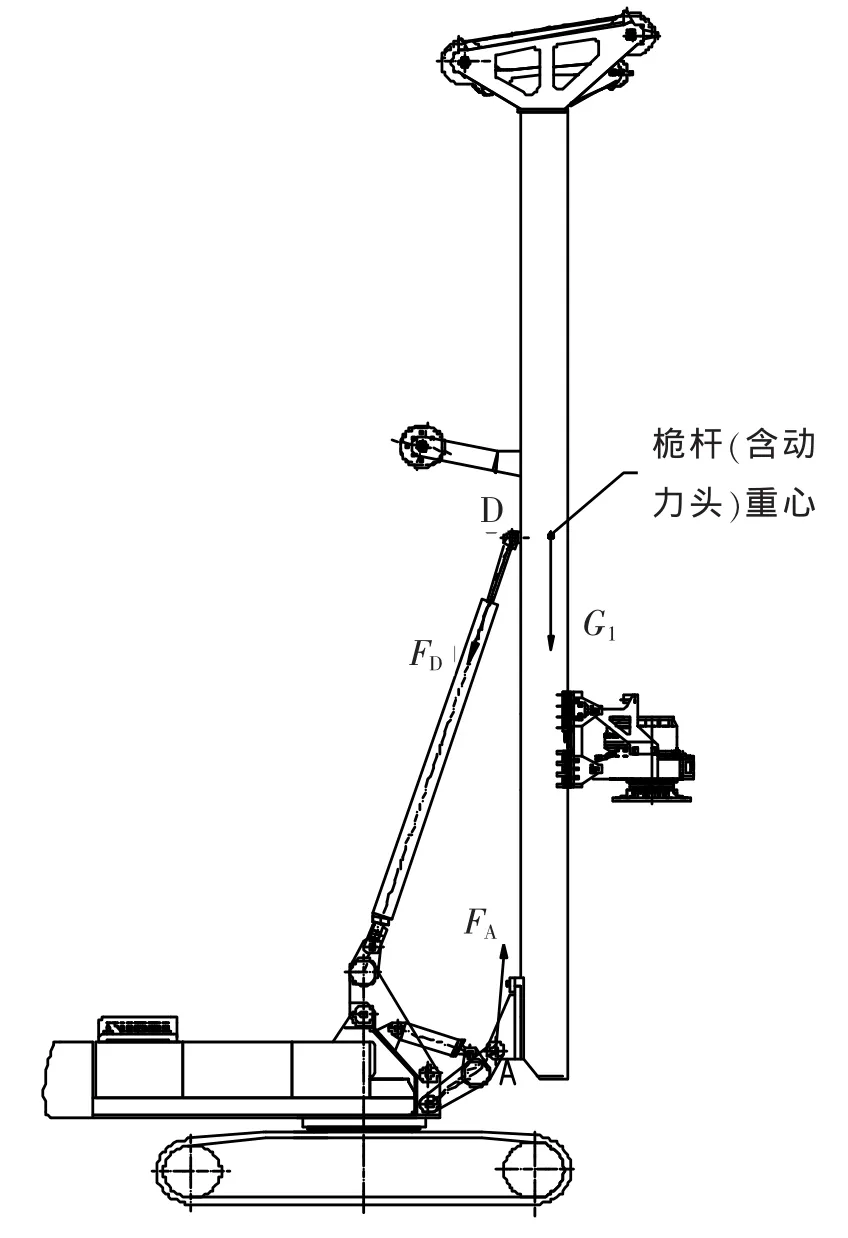
图6

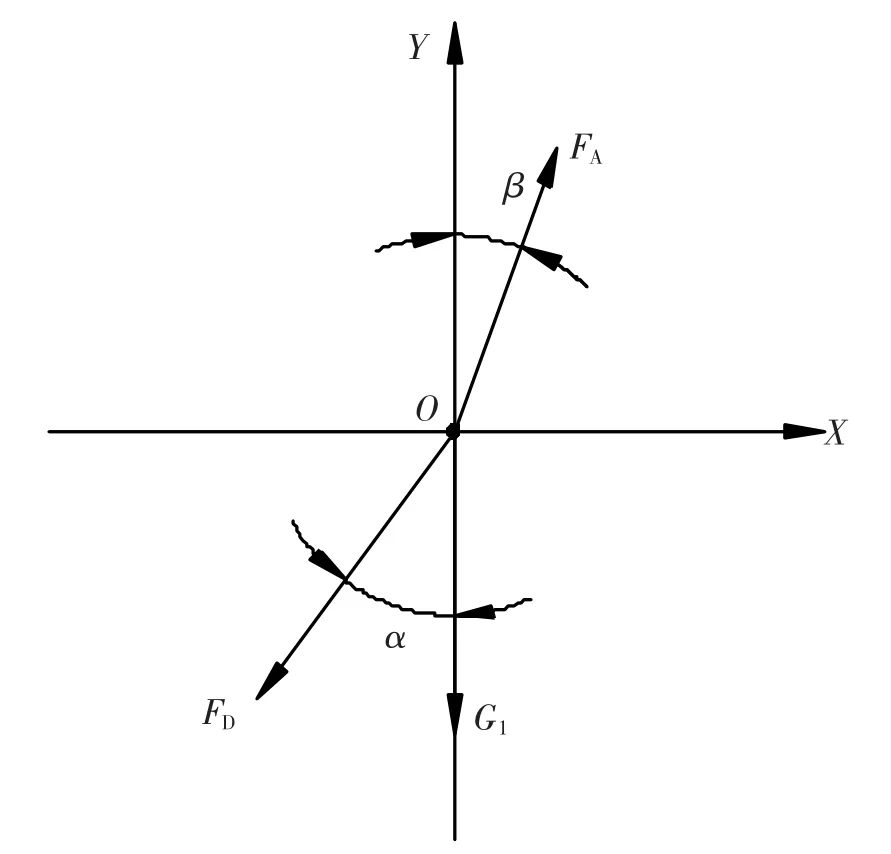
图7

图6、图7中

FD——在提升卷扬钢丝绳不受力的工况下，桅杆在桅杆油缸铰接点D处所受的力

FA——在提升卷扬钢丝绳不受力的工况下，桅杆在动臂连接处铰接点A处所受的力

G1——桅杆重量，包括动力头在内

α——FD与铅垂线的夹角

β——FA与铅垂线的夹角

根据受力图7，列平衡方程

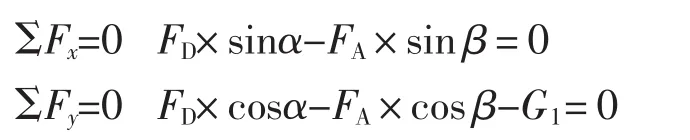
求解上述方程组，可以得到在提升钢丝绳不受力的工况下，桅杆油缸所受的拉力FD

第三步：导出受力分析数学模型

（1）桅杆铰接点D的受力分析数学模型

将所求得的FD的结果，带入方程6，从而可以求得在提升工况下，桅杆在桅杆油缸铰接点D处所受的拉力Fd，即为桅杆油缸铰接点D的受力分析数学模型。

（2）动臂铰接点A的受力分析数学模型

将求得的Fd数学模型分别带入方程1和方程2，从而可以求出FAx、FAy，得到桅杆上的动臂铰接点A的受力分析数学模型。

3 结束语

综上所述，在求解桅杆铰接点的受力分析数学模型时，用到了理论力学、弹塑性力学和液体的弹性模量的理论，通过这些理论的贯穿应用，可以解决工程设计人员在大部分工程机械设计过程中的零部件受力分析问题，为机械设计工程师在设计选型、校核、有限元分析边界条件计算、有限元运算结果分析校核以及优化设计等方面提供理论参考。

[1]Dr.–Ing，H.Willms.Skript Festig keit slehre[M].2008.9.

[2]哈尔滨工业大学理论力学教研室.理论力学[M].北京：高等教育出版社，第七版，2011.

[3]陈惠发等著，余天庆等编译.弹性与塑性力学[M].北京：中国建筑工业出版社，2003.

[4]张凤兰，计新.液体的体积弹性模量测定[J].延边大学学报(自然科学版)，第28卷第三期，2002.9.