基于CCA和WRM视窗分析的中国R＆D投入绩效评价研究

尹伟华，袁 卫

(1.中国人民大学统计学院，北京100872;2.安徽财经大学统计与应用数学学院，安徽蚌埠233030)

一、引 言

R＆D活动作为科技活动的基础和核心，不仅是衡量一个国家和地区科技发展水平、科技活动结构、科技含量的重要指标，也是反映一个国家和地区自主创新能力的重要内容。多年来，中国一直加大R＆D资源投入力度，使得R＆D资源总量与强度都有了很大的提高。 其中，R＆D人员全时当量由1991年的67.05万人年上升到2010年的255.38万人年，R＆D强度(R＆D经费/GDP)也由1991年的0.69%上升到2010年的1.76%，这些都有效地促进了中国科技活动的开展，为社会经济持续、健康的发展奠定了重要基础。但同时也应看到，中国的R＆D活动发展还相对缓慢，与发达国家还存在一定的差距，这与中国现在所处的经济大国地位是不太相符的。因此，在中国处于经济发展方式转变的关键时期，如何在现有科技、经济资源有限的情况下，提高R＆D资源利用水平和创新效率，对加快中国经济发展方式的转变，提高经济发展的质量，增强国际竞争力具有十分重要的理论和实际意义。

二、文献综述

近年来，R＆D投入绩效问题受到学术界的广泛关注，并取得了丰硕的研究成果。文献按研究方法的不同主要有2种:一是基于参数技术的随机前沿分析法(SFA)，即运用计量经济学的方法估计各投入要素的参数，并在此基础上估计出产出效率。如:Zhang et al使用SFA测算了中国不同产权类型企业的R＆D效率，并进行了对比分析［1］。Wang运用超越对数随机前沿函数评价了国家层面的R＆D投入绩效［2］。白俊红等采用面板随机前沿函数模型，实证测评了中国各地区R＆D的创新效率与全要素生产率的增长情况［3］。刘和东应用面板SFA分析了中国区域的 R＆D效率及其影响因素［4］。由于R＆D活动是多投入多产出的复杂过程，而SFA只能处理单一产出，且需要正确设定函数的形式，导致了该方法的应用存在一定的局限性;二是基于非参数技术的数据包络分析法(DEA)，即将投入产出点映射到空间上，以最大产出或者最小投入为效率边界，测算出各点与边界之间的距离差距程度。如:Korhonen用DEA方法对芬兰大学的R＆D效率进行了评估［5］。Sena利用DEA比较分析了意大利不同类型企业间的R＆D效率，指出高技术企业对非高技术企业的效率具有一定的溢出效应［6］。Gaimon＆Morton运用DEA模型对美国高技术产业的R＆D效率进行了估算和排名［7］。Lee＆Park采用DEA方法对R＆D绩效展开了国际比较［8］。Wang＆Huang考虑了R＆D活动外部环境因素的影响，使用三阶段DEA方法对OECD各国的R＆D效率进行了测度［9］。Chen＆Yeh分别运用CCR和BCC估算了1991－1999年台湾高技术行业的 R＆D效率［10］。Lee et al采用DEA方法对国家不同类别的R＆D项目进行了效率评价［11］。Guan＆ Chen通过构建两阶段DEA模型，全面分析了中国区域高技术产业的R＆D效率［12］。Li et al分别运用基于合作博弈和非合作博理论的两阶段DEA模型评价了中国区域的R＆D效率问题［13］。虽然DEA具有不需要预先确定函数形式，处理数据量纲和确定指标权重等优点，但由于传统DEA属于径向和线性分段形式的度量，没有考虑松弛量(slack)和时间维度的影响，从而可能会造成效率测度的结果是有偏的［14］。

综观上述文献，本文试图运用综合考虑松弛量和时间维度的 WRM(Weighted Russell Measure，WRM)视窗分析模型研究中国的R＆D投入绩效问题，以期达到弥补现有文献的不足，及为现有文献提供有益的补充。文章后续部分结构安排如下:第二部分详细简述研究方法;第三部分为样本和数据的说明;第四部分为具体的实证分析;最后是结论和相应的政策启示。

三、WRM视窗分析模型

RM模型(Russel measure，RM)最初是由Fare＆ Lovell［15］提出，虽然该模型是基于投入(或产出)不同比例的最大缩减(或扩大)，解决了传统DEA模型的径向问题。但由于RM模型并没有考虑各投入(或产出)要素的相对权重，从而导致RM模型也存在一定的缺陷［16］。同时，缺乏时间维度的RM模型，也难以进行相应的动态性和稳定性分析，使得评价结果不够全面和客观。鉴于此，本文综合加权RM(WRM)模型和时间维度构建投入导向型的WRM视窗分析模型。

(一)WRM视窗分析模型

假设在DMUn(n=1，2，…，N)中，每个DMU有m 个投入xi(i=1，2，…，M)和s个产出yr(r=1，2，…，S)，其投入产出向量分别为:Xn(x1，x2，…，xM)T;yn(y1，y2，…，yS)T。若生产过程中各投入要素的相对权重为 wi(i=1，2，…，M)，则基于可变规模报酬(Variable Returns to Scale，VRS)的WRM模型为:

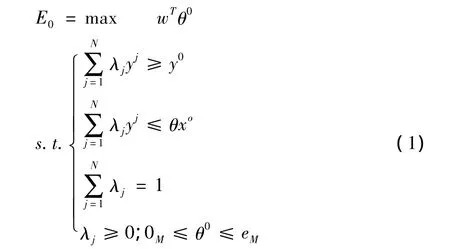
其中，wT=(w1，w2，…wM)表示各投入要素的权重向量，θ0=(θ1，θ2，…，θM)T表示各投入要素的缩减比例，λ0表示生产过程中密集度的密度向量，0M表示零向量，eM=(1，1，…，1)T表示单位向量，θx0(θ1x1，θ2x2，…，θMxM)T表示投入要素的投影向量。若λ0*和θ0*为模型(1)的最优解，则DMU0的效率等于各投入要素缩减比例的加权算术平均，即若效率值等于1，则称DMU0是有效的。

由于上述WRM模型主要用于截面数据分析，即对被评价的DMU与同时期的其他DMU进行比较，其没有考虑时间的影响。但从时间角度来看，截面数据分析得出的结论容易出现偏差，因为某些资源在早期看来可能是浪费的，但实际上这些资源部分会产生未来的收益。由于面板数据测算的效率不仅反映了与其他DMU的比较结果，而且也反映了自身效率的变动情况。因此，面板数据分析更能反应DMU的实际效率。

Charnes et al［17］提出的视窗分析模型(Window Analysi，WA)，主要是对面板数据进行效率测算。WA的基本原理是:将不同时期的同一个DMU当作不同单元来处理。其首先确定视窗内的时期长度(窗宽)，然后再对窗宽内的每一个DMU进行效率评估。在视窗分析中，视窗每滑动一次就将最早的一个时期从视窗中去掉，而增加下一个新时期，这与统计学中的平滑指数类似［18］。

设在时间t(t=1，2，…，T)内有n个DMU(n=1，2，…，N)，则DMUn在时间t的投入向量为(x1t，x2t，…，xMt)T，产出向量为=(y1t，y2t，…，ySt)T。同时，假设窗宽为w(1≤w≤T)，视窗时间从k(1≤k≤T－w+1)开始，则第kw个视窗共有n×w个DMU，且其视窗分析的投入产出矩阵可表示为:

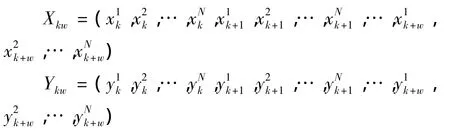
关于窗宽的选择至今还没有一个统一的标准，但在实际处理中，一般都取3，这与Charnes et al的做法是一致。

(二)权重设定

根据Ruggiero＆Bretschneider等相关研究，投入要素的相对权重可以用相应要素的标准化弹性系数所占比重来表示［16］。但由于R＆D活动是多投入多产出过程，弹性系数并不能直接利用C－D生产函数进行估算。因此，本文首先在C－D生产函数的基础上，扩展得到一个多投入多产出的生产函数模型:

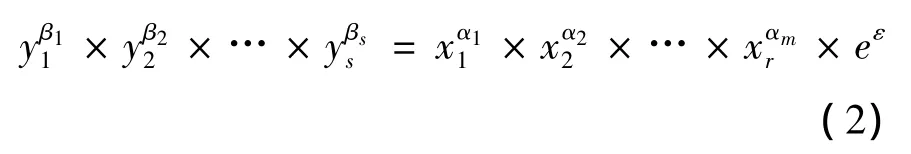
其中，eε为随机误差项。同时对上述生产函数两边取对数，可得:

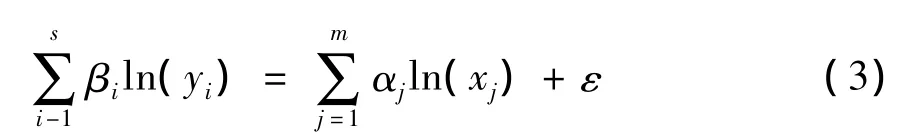
由于R＆D活动中投入、产出间存在严重的相关性，显然采用经典的多元回归对(3)式进行参数估计将存在严重的伪回归问题。因此，本文采用Vinod提出的典型相关分析法(Canonical Correlation Analysis，CCA)对上述多投入多产出生产函数进行参数估计［19］。

CCA是研究两组变量之间相关关系的一种多元统计方法，其基本思想是:首先在每组变量中找出变量间的线性组合，使其具有最大相关性，同理再找出第二对最大相关的线性组合，且其分别与第一对线性组合不相关，如此重复下去，直到两组变量间的相关性被提取完毕为止。从而关于两组变量间的相关关系的研究转变为对由这两组变量形成的线性组合的最大相关的研究，以减少变量研究的个数。

运用CCA对(3)式进行参数估计，将产生两个分别关于投入产出观测变量的线性组合，可以表示为:

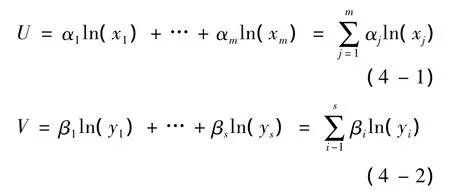
令 L=(α1，α2，…，αm)、M=(β1，β2，…，β*s)，根据CCA结论，取:

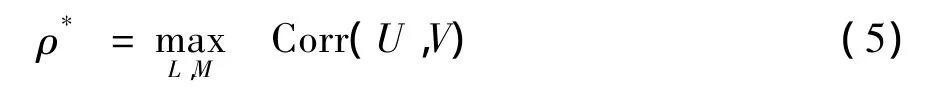
将(4－1)、(4－2)、(5)式带入(6)式就得到(3)式的估计式:

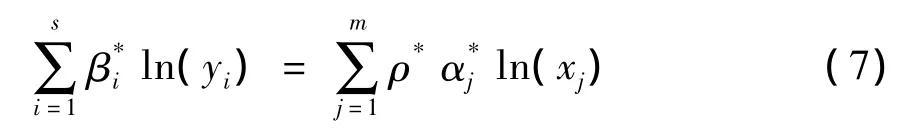
根据 Gyimah－Brempong＆ Gyapong、Ruggiero［20－22］等定义，投入与产出间的边际产出弹性关系为:

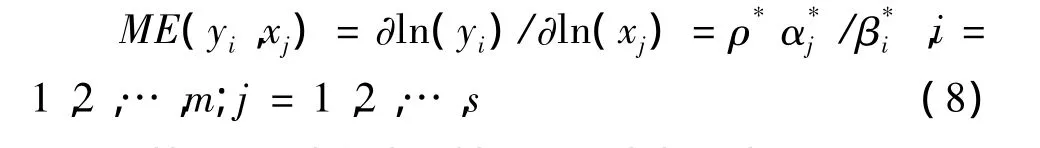
则投入要素的相对权重可以表示为:

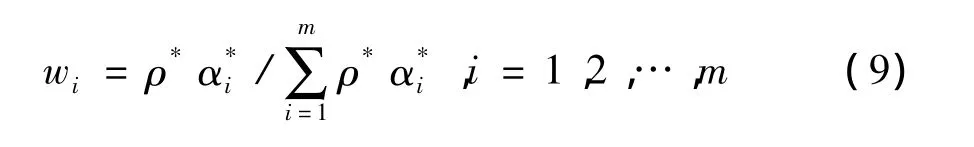
四、样本和数据说明

考虑到不同的分析模型，本文所使用的样本数据主要来源于两个方面:

一是基于CCA模型，研究样本为1991－2010年全国的R＆D投入产出数据。其中，R＆D投入包括R＆D资本存量(单位:亿元)和R＆D人员全时当量(单位:人年);R＆D产出包括专利申请受理数(单位:件)、国外主要检索工具收录的科技论文数(单位:篇)和技术市场成交合同金额(单位:亿元)。由于中国现行的统计年鉴没有R＆D资本存量数据，根据 Goto ＆ Suzuki［23］和 Griliches［24］等相关研究，本文采用永续盘存法估算R＆D资本存量。计算公式为:

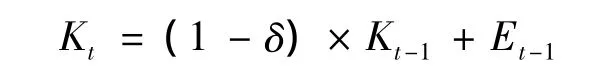
式中，K和kt－1分别为第t和(t－1)期的资本存量;δ为折旧率，本文参考国际通行做法，将中国折旧率设定为 15%［25］;Et－1为第(t－ 1)期的实际R＆D经费支出。由于中国连续的R＆D经费支出数据始于1991，故本文采用朱平芳和徐伟民［26］构造的R＆D价格指数，以1991年为基期，对名义R＆D经费支出进行平减。

在估算基期资本存量时，本文假设R＆D资本存量的增长率等于R＆D经费的增长率，则基期资本存量的估算公式为:K0=E0/(g+δ)。

式中，K0为基期资本存量，E0为基期实际R＆D经费支出，g为考察期内实际R＆D经费支出的平均增长率，δ为折旧率。

同时，由于上述样本期时间跨度较长，可能会由于通货膨胀或紧缩造成核算结果的虚增或虚减。因此，为了准确反映R＆D活动的真实状况，本文采用GDP平减指数对技术市场成交合同金额进行调整，以剔除价格因素的影响。

二是基于WRM视窗分析模型，研究样本为2004－2008年中国各省、市、自治区的R＆D投入产出数据①由于西藏自治区变量异常值较多，且存在数据缺失，故样本剔除西藏自治区。。其中，R＆D投入包括R＆D经费内部支出(单位:万元)和R＆D人员全时当量(单位:人年);R＆D产出包括专利申请受理数(单位:件)、国外主要检索工具收录的科技论文数(单位:篇)和技术市场成交合同金额(单位:万元)。在R＆D投入绩效评价过程中，由于R＆D投入产出之间存在一定的时滞性，参考 Adams ＆ Griliches，Guellec 等［27－28］相关研究，本文选取1年滞后期。即R＆D投入数据选取2004－2008年，产出数据选取2005－2009年。数据主要来源于《中国科技统计年鉴1991－2011》、《中国统计年鉴2011》。

五、实证分析

(一)弹性分析及权重选择

基于CCA模型，利用SPSS 16.0软件，可以估算出1991－2010年中国R＆D资源的边际产出弹性，以此确定WRM视窗分析模型中投入要素的相对权重。

表1 典型相关系数的统计检验

表2 典型变量对观测变量的贡献率及累计贡献率

由表1和表2可知:第1对典型变量的相关系数高达0.998，且在1%的水平上高度显著。同时，第1对典型变量对投入产出观测变量的解释率超过97%以上，说明第1对典型变量包含了原始变量的绝大部分信息，能对原观测变量起到很好的代表作用。所以，本文选取第1对典型变量进行分析是适合的。

在典型变量确定后，可以得到投入产出变量标准化的典型系数。则，第1对典型变量的表达式为:

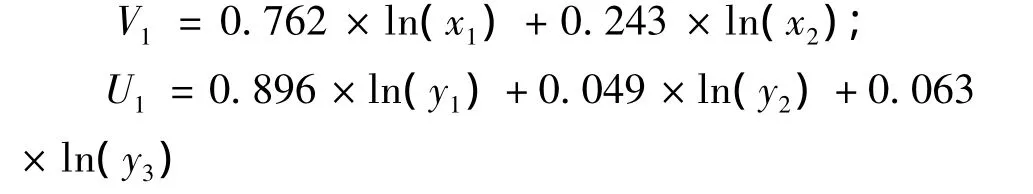
根据(8)式可以估算出中国R＆D活动投入要素的边际产出弹性，如表3所示。

由表3可知:R＆D资本存量相对于R＆D人员而言，具有较高的边际产出弹性，说明R＆D资本存量在R＆D活动中具有核心作用。虽然样本期间中国R＆D经费投入以年均22.44%的速度增长，但其占GDP的比例同发达国家相比，还存在一定差距。因此，中国应继续加大R＆D经费投入力度，以促进R＆D活动的产出成果，提高R＆D资源的利用效率。

在R＆D活动的各种产出成果中，R＆D资本存量和R＆D人员对科技论文发表数量的产出弹性最大，分别为15.5199、4.9493，说明现有的 R＆D 资源有效地推动了中国基础研究的发展。由于基础研究是新知识产生的源泉和新发明创造的先导，是地区长期科技发展和区域竞争力提升的重要基础，而基础研究的产出弹性最大，表明增加R＆D资源将直接影响到中国科技原始创新能力水平的提高。

表3 R＆D活动资源投入要素边际产出弹性

R＆D资本存量和R＆D人员对专利申请受理量的产出弹性最小，分别为 0.8487、0.2707，说明相对于其他R＆D产出成果，现有的R＆D资源并未有效地促进专利成果的快速增长。这主要是由于中国处于发展中国家，其技术能力有限，开始主要是模仿发达国家的先进技术，加之，R＆D创新活动的收益虽大，风险却很高。因此，从技术层面上来说，发展中国家更关注模仿，尤其在知识产权保护力度不足的情况下，模仿显然比自己创新更为合算［29］。

最后，根据(9)式计算出R＆D活动投入要素的相对权重。R＆D经费的相对权重为:w1=0.758;R＆D人员的相对权重为:w2=0.242。

(二)效率分析

基于WRM视窗分析模型，利用Matlab 2007软件，测算出2004－2008年中国各省区R＆D投入效率，结果如表4所示。其横向数值反映每个省区R＆D投入效率的时间变化，纵向数值反映同一年份R＆D投入效率的空间变化。

总体来看，2004－2008年中国各省区R＆D投入效率均值只达到0.7539，这意味着即使R＆D投入平均消减24.61%，仍然能保持既定的期望产出水平。其中，低于效率均值的省区有13个，占省区总数的43.33%，且最大效率值为1.000，最小效率值为0.3628，这些都表明中国R＆D投入绩效存在明显的地区差异。具体来看，上海处于R＆D活动的最优前沿面上，成为其他省区的学习标杆，其考察期内的效率值均为1.000。效率较高的省区还有浙江、北京、湖北、海南和广东，其效率均值均超过0.9500，表明这些省区的R＆D资源利用都已接近最优前沿面，改进空间较小。而考察期内效率排名最后几位的省区基本没有发生变化，依然是宁夏、河北、山西和江西等，相对于效率较高的省区而言，这些省区的R＆D投入存在严重的资源浪费。

从变化趋势来看，考察期内中国的R＆D投入效率表现出一定波动后的缓慢下降，其值由2004年的0.7865下降到 2006年的 0.7409，而后又上升到2007 年的 0.7627，最后下降到 2008 年的 0.7291。具体各省区而言，R＆D投入效率的演化趋势较为多变。如:北京、浙江、上海等省区基本一直维持原有的高效率水平;四川、辽宁、青海、江苏、吉林等省区表现为明显的上升趋势;江西、河北、内蒙古、贵州、安徽、新疆等省区呈现出一定的下降趋势。

从差异性来看，考察期内中国各省区之间的R＆D投入效率差异正呈现出缓慢的扩大趋势，并不存在“收敛”现象。R＆D投入效率的标准差由2004年的0.1832，上升到2008 年的0.2129，其平均标准差也达到0.1902，再次验证了中国R＆D投入效率存在明显的地区差异。具体每个省区而言，不同时间的R＆D投入效率差异变化也较大。如:上海、浙江、北京、吉林、福建、湖北等省区的时间变化较小;而山西、重庆、新疆、内蒙古、江苏、青海等省区的时间变化较大。

为进一步对中国R＆D投入效率的水平性和稳定性进行比较分析，本文将效率均值分为高效率和低效率两个等级，效率值属于［0.82，1］的为高效率地区，［0，0.82)的为低效率地区;同时根据标准差的大小，也可分为高稳定性和低稳定性两个等级，标准差属于［0.06，1］的为高稳定性地区，［0，0.06)的为低稳定性地区。按照这一标准划分，得到R＆D投入绩效的象限图(如图1):

图1 中国R＆D投入效率水平性和稳定性的象限图

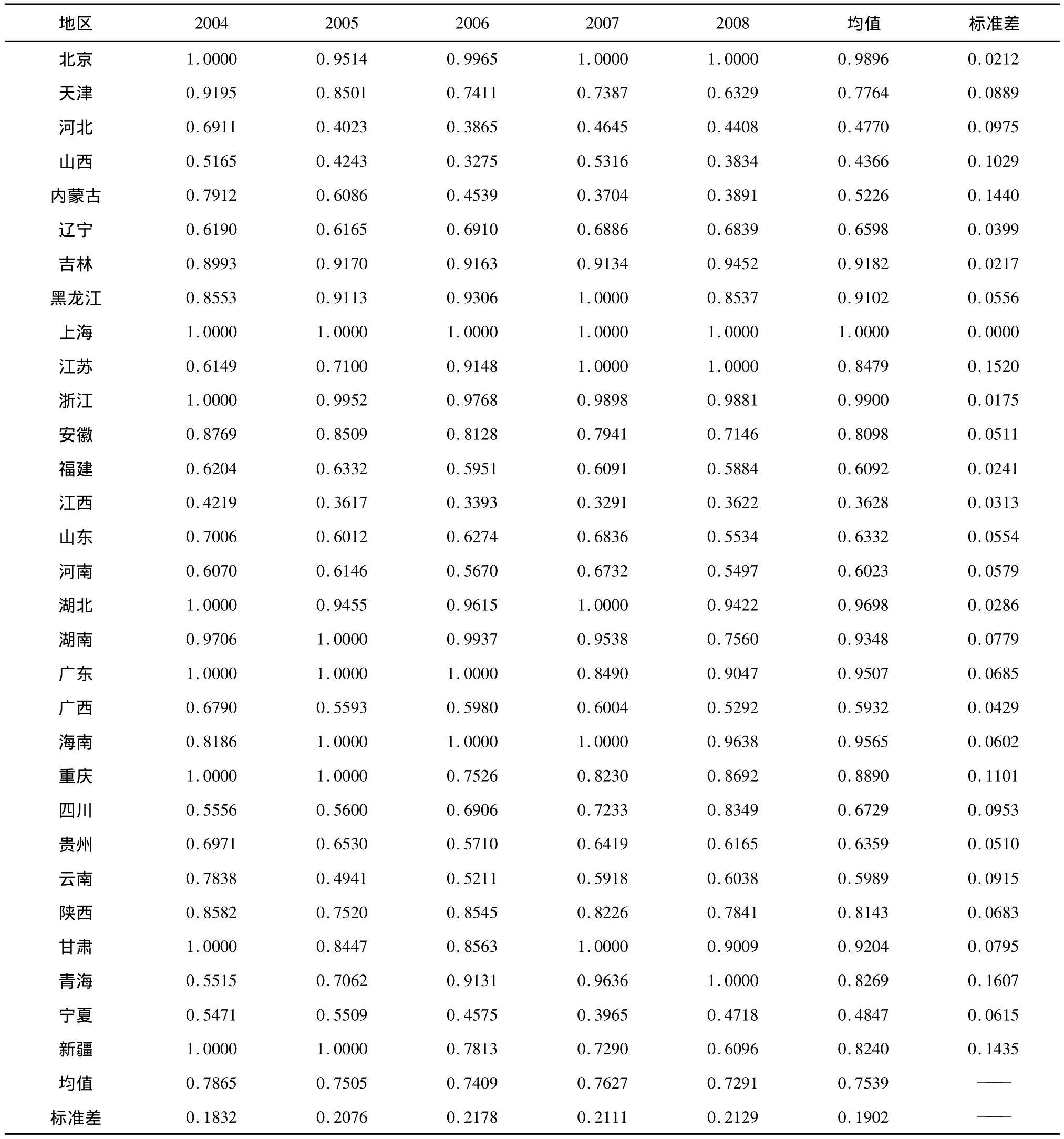
表4 2004－2008年中国各省区R＆D投入绩效评价结果

第一象限为高效率和低稳定性的地区，处于该象限的地区有湖南、甘肃、重庆、新疆、江苏、青海。这类地区虽然考察期内的R＆D投入效率较高，但不同年份的效率水平变化很大，存在较大的波动。由于该类地区存在一定的不稳定因素，例如:R＆D人员流动性较大、缺少稳定的R＆D融资体制、不合理的R＆D投入结构等，使得不同时期的R＆D投入效率产生较大的波动。因此，该类地区应在继续保持R＆D投入较高效率的同时，找出不稳定因素，保持R＆D投入的持续、高效转化。

第二象限为低效率和低稳定性的地区，处于该象限的地区有云南、四川、河北、山西、天津、内蒙古。这类地区不仅考察期内的R＆D投入效率较低，且不同年份的效率水平差异也较大。由于该类地区一方面投入大量的R＆D资源但又不注重有效管理，另一方面本身也存在着影响R＆D投入转化的不稳定因素，导致了低效率和低稳定性的双重困境。因此，该类地区应从R＆D资源有效管理和消除不稳定因素等多方面入手，才能从根本上解决双重低下的困境。

第三象限为低效率和高稳定性的地区，处于该象限的地区有福建、江西、辽宁、广西、贵州、安徽、河南、宁夏、山东、陕西。这类地区虽然考察期内的R＆D投入效率较低，但不同年份的效率水平变化不大，基本保持原有的低效水平。由于该类地区的R＆D活动运行环境相对较差，存在R＆D资源的盲目投资，即不注重投资质量，或存在对外部科技成果的较强依赖性，忽略了R＆D投入转化效率等，导致该类地区的持续低效性。因此，该类地区首先应改善R＆D运行环境，在打破持续低效状态的基础上，调整和优化R＆D资金投入结构，设立R＆D活动的风险投资机制及基金，制定良好的激励及奖励政策，提高科研人员的积极性，提高R＆D资源转变成科技成果的数量和质量。

第四象限为高效率和高稳定性的地区，处于该象限的地区有上海、浙江、北京、广东、吉林、湖北、黑龙江、海南。这类地区考察期内的R＆D投入效率较高，且不同年份的效率水平差异不大，一直保持较高的效率水平。由于该类地区主要为发达的东、中部地区，其拥有相对较好的经济实力、丰富的科研力量和发达的市场经济体制等，对R＆D资金和技术人才等方面具有很强的吸引力，为R＆D投入转化奠定了坚实的基础。其中，海南的R＆D资源投入规模相对较小，但是在资源利用上却表现出一致的高效性。

六、小结与启示

为了解决传统DEA模型没有考虑松弛量和时间维度等问题，本文首先构建CCA模型和WRM视窗分析模型，并在此基础上，以不同层面的R＆D投入产出数据为样本，对中国R＆D投入绩效进行了较为全面的评价分析。研究结果表明:(1)R＆D资本存量相对于R＆D人员而言，具有较高的边际产出弹性，即R＆D资本存量在R＆D创新活动中具有核心作用;(2)在R＆D活动产出中，R＆D资源对科技论文发表数量的产出弹性最大，而对专利申请受理量的产出弹性最小，说明现有的R＆D资源有力地推动了中国基础研究的发展，但并未有效地促进专利成果的快速增长。(3)2004－2008年中国R＆D投入效率均值较低，且表现出一定波动后的缓慢下降。具体各省区而言，R＆D投入效率的演化趋势则较为多变。(4)考察期内中国各省区间的R＆D投入效率差异呈现出缓慢的扩大趋势，并不存在“收敛”现象。具体每个省区而言，不同时间的R＆D投入效率差异变化也是很大的。(5)从R＆D投入效率水平性和稳定性的比较分析看，除了上海、浙江、北京、吉林、湖北、黑龙江、海南、广东的R＆D活动具有高效率和高稳定性外，大部分地区的R＆D活动都表现为双重低下或一高一低。

上述结论为我们制定相应的经济政策提供一定的指导意义:中国各地区应继续加大对R＆D经费的投入力度，促进R＆D活动的产出成果，提高R＆D的投入产出效率。在增加R＆D经费的同时，也应注意R＆D经费与R＆D人员的合理配置，避免R＆D经费配置的无效率;在现阶段R＆D资源有限的情况下，中国应更加注重R＆D投入产出的效率问题，这不仅有利于R＆D资源的有效利用，更有益于社会经济的持续、健康发展;根据R＆D投入效率水平性和稳定性的象限图，中国各地区可针对自身所处的位置，实现不同的效率提升路径。如，新疆应在继续保持R＆D投入产出较高效率的同时，找出R＆D活动中的不稳定因素，促进R＆D资源的持续、高效转化;江西重点是改善R＆D活动的运行环境，打破持续的低效状态，并在此基础上，调整和优化R＆D资金投入结构，制定良好的激励及奖励政策，提高科研人员的积极性，提高R＆D资源转化的数量和质量等。

［1］Zhang Anming，Zhang Yimin，Zhao R.A study of the R＆D efficiency and productivity of Chinese firms［J］.Journal of Comparative Economics，2003，31(3):444 －464.

［2］Wang E C.R＆D efficiency and economic performance:A cross－ country analysis using the stochastic frontier approach［J］.Policy Modeling，2007，29(2):345 －60.

［3］白俊红，江可申，李婧.中国地区研发创新的相对小了与全要素生产率增长分解［J］.数量经济技术经济研究，2009(3):139－151.

［4］刘和东.中国区域研发效率及其影响因素研究——基于随机前沿函数的实证分析［J］.科学学研究，2011(4):548－556.

［5］Korhonen P，Tainio R，Wallenius J.Value efficiency analysis of academic research［J］.European Journal ofOperational Research，2001，130(1):121 －132.

［6］Sena V.Total factor productivity and the spillover hypothesis:Some new evidence［J］.International Journal of Production Economics，2004，92(1):31 －40.

［7］Gaimon C，Morton A.Investment in facility changeover flexibility for early into high － tech markets［J］.Production and Operations Management，2005，14(2):159 －174.

［8］Lee H，Park Y.An international comparison of R＆D efficiency:DEA approach［J］.Asian Journal of Technology Innovation，2005，13(2):207 －222.

［9］Wang E C，Huang W.Relative efficiency of R＆D activities:A cross－country study accounting for environmental factors in the DEA approach［J］.Research Policy，2007，36(2):14－28.

［10］Chen C J，Yeh Q J.A comparative performance evaluation of Taiwan’s high － tech industries［J］.International Journal of Business Performance Management，2006，7(1):16－33.

［11］Lee H，Park Y，Choi H.Comparative evaluation of performance of national R＆D programs with heterogeneous objectives:A DEA approach［J］.European Journal of Operational Research，2009，196(3):847－855.

［12］Guan Jiancheng，Chen Kaihua.Measuring the innovation production process:A cross－region empirical study of China’s high － tech innovations［J］.Technovation，2010，30:348 －358.

［13］Li Yongjun，ChenYao，Liang Liang，et al.DEA models for extended two－ stage network structures［J］.Omega，2012，40(5):611 －618.

［14］Fried H O，Schmidt S S，Yaisawarng S.Incorporating the operating environment into a nonparametric measure of technical efficiency［J］.Journal of Productivity Analysis，1999，12(3):249 –267.

［15］Fare R，Lovell C A K.Measuring the technical efficiency of production［J］.Journal of Economic Theory，1978，19(1):150 －162.

［16］Ruggiero J，Bretschneider S.The weighted Russell measure of technical efficiency［J］.European Journal of Operational Research，1998 ，108(2):438－451.

［17］Charnes A，Clark C T，Cooper W W，et al.A developmental study of data envelopment analysis in measuring the efficiency of maintenance units in the US air forces［J］.Annals of Operation Research，1984，2(1):95 －112.

［18］Charnes A，Cooper W W，Lewin A，et al.Data envelopment analysis:Theory，methodology and applications［M］.Norwell:Kluwer Academic Publishers，1994.

［19］Vinod T.Canonical ridge and econometrics of joint production［J］.Journal of Econometrics，1976，4(2):147－166.

［20］Gyimah－Brempong K，Gyapong A O.Characteristics of education production functions:An application of canonical regression analysis［J］.Economics of Education Review，1991，10(1):7 －17.

［21］Ruggiero J.Efficiency of education production:An analysis of New York school districts［J］.The Review of E－conomics and Statistics，1996，78(3):499 －509.

［22］Ruggiero J.A new approach for technical efficiency estimation in multiple output production ［J］.European Journal of Operational Research，1998，111:369 －380.

［23］Goto A，Suzuki K.R＆D capital，rate of return on R＆D investment and spillover of R＆D in Japanese manufacturing industries［J］.Review of Economics and Statistics，1989 ，71(4):555 －564.

［24］Griliches Z.Patents statistics as economic indicators:A survey［J］.Journal of Economic Literature，1990 ，28(4):1661－1707.

［25］Hall B H，Mairesse J.Exploring the relationship between R＆D and productivity in French manufacturing firms［J］.Journal of Econometrics，1995，65(1):263－293.

［26］朱平芳，徐伟民.政府的科技激励政策对大中型工业企业R＆D投入及其专利产出的影响——上海市的实证研究［J］.经济研究，2003(6):45－53.

［27］Adams J D，Griliches Z.Research productivity in a system of universities［A］.Encaoua D.The economics and econometrics of innovation［M］.Boston:Kluwer Academic Publishers，2000.

［28］Guellec D，van Pottelsberghe de la Potterie B.From R＆D to productivity growth:Do the institutional settings and the source of funds of R＆D matter?［J］.Oxford Bulletin of Economics and Statistics，2004，66(3):353－378.

［29］Mazzoleni R，Nelson R R.The benefits and costs of strong patent protection:A contribution to the current debate［J］.Research Policy，1998，27(3):273 －284.