异体互对偶变换

文钦若

(河北大学 河北 保定 071002)

1 引言

有一种对称性可称为对偶对称性，而对偶对称性又可分为两种，即两个体系之间的相互对偶与同一个体系自身的对偶，此文只讨论两个体系之间的相互对偶，也可称为异体互对偶.异体互对偶主要表现在图形与关系式两个方面，在物理学中首先注意的往往是关系式.如果两个物理体系A与B互对偶，则体系A中物理量之间的关系式与体系B中对偶物理量之间的关系式通常具有相同的形式.但应注意，如果体系A与体系B具有某些形式相同的关系式，则并不表示这两个物理体系就一定是互对偶的.对于异体互对偶而言，所谓对偶原理是指由一个体系中的规律可以推知对偶体系中的规律.如果不能由一个体系中的规律全面而正确地推知另一个体系中的规律，则即使这两个体系中存在某些形式相同的关系式，也不能认为这两个体系是互对偶的.对于互对偶的两个物理体系，构成这两个体系的各元素以及描写这两个体系的各物理量都有一一对应的对偶关系，根据这些对偶关系便可以将其中的一个物理体系变换为另一个物理体系，这种变换便称为互对偶变换.

2 互对偶的线性电路

2.1 耗能元件与储能元件

电阻R是耗能元件，设流过R的电流为I，则R所消耗的功率为

P=RI2

(1)

电阻的倒数称为电导，电导G′也可视为耗能元件，设G′两端的电压为U′，则G′所消耗的功率为

P′=G′U′2

(2)

式(1)与式(2)有相同的形式.电感L是储存磁场能的元件，设流过L的电流为I，则L所储存的能量为

(3)

电容C′是储存电场能的元件，设C′两端的电压为U′，则C′所储存的能量为

(4)

式(3)与式(4)具有相同的形式.可认为(1)～(4)式为引入对偶量提供了重要依据.

2.2 基尔霍夫定律

由于线性放大器以及线性双口网络(也称为四端网络)可以用等效电路代替，所以只考虑由电阻R，电感L，电容C以及电压源、电流源所构成的线性网络[1].对于一个完整的线性网络A，其物理规律可以用基尔霍夫方程组描写

(5)

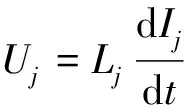
l=m+n-2

(6)

通过对偶变换可以得到网络A的对偶网络B.A与B的元件数应相等.由(1)～(4)式可推知基尔霍夫第一定律与第二定律应互对偶，则从A变到B的对偶变换应为

(7)

将上式应用到(5)式得

(8)

上式便是描写网络B的基尔霍夫方程组.

类似于一个带小孔的弹性球面可以展开为一个平面，有一些电路图也可以展开为平面电路图.平面电路图的特点是：在平面上没有交叠的元件与交叠的连线.对于两个对偶的平面电路图，如果将这两个图A与B叠在一起，由于A与B的元件数相等，则总可以使对偶元件彼此交叠，这时便可看出，A图中的每一个网孔中必有B图中的一个节点；B图中的每一个网孔中也必有A图中的一个节点，即节点与网孔对偶，且节点处的支路数与对偶网孔的支路数(边数)相等.因此，从已知网络A可以用下述作图方法求出其对偶网络B：在A图的每一个网孔中取一点作为B图的节点，用与A图中各元件交叠的对偶元件将A图中对应元件两边网孔中的节点连接在一起便可以得到B图.

对于两个电阻(或其他两个线性元件)串联的电路，此电路有两个端点，所以不是完整的电路图.为了得到此电路的对偶电路，可以用一条波浪线将两个端点连在一起而构成一个完整电路，这条波浪线便代表一条未知的支路.然后用上述方法便可得到其对偶电路图，从而得知两个电阻的串联与两个电导的并联是互对偶的电路.对于Π型(或T型等)线性双口网络，可以用一条波浪线(代表未知的输入支路)将输入口的两端连在一起，用另一条波浪线(代表未知的负载支路)将输出口的两端连在一起，从而构成完整网络.然后用上述方法也可得到其对偶电路图，从而可得知Π型线性双口网络与T型线性双口网络互对偶.

2.3 对偶电路举例

考虑互对偶的并联调谐电路与串联调谐电路.设并联调谐电路如图1所示.

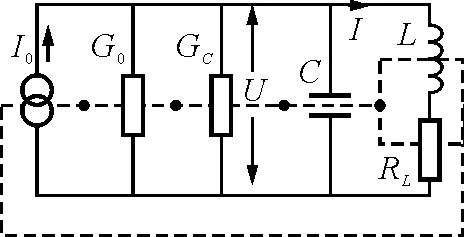
图1

上图中，虚线表示其对偶电路的形状.I0=Iasinωt，G0为正弦电流信号源I0的内电导，RL为电感L的绕线电阻，电导Gc称为电容C的电漏.根据图1中的虚线与对偶变换可得到图1的对偶电路图2为

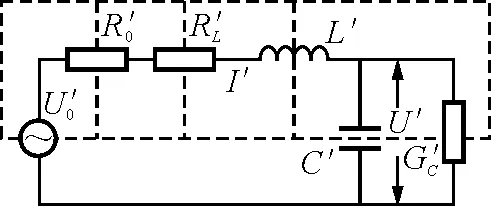
图2

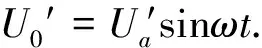
(9)

(10)

3 异体互对偶变换的特点

(1)对偶量的量纲不一定相同.在(7)式中，电压与电流、电阻与电导、电感与电容的量纲都是不同的，但网孔数与节点数的量纲是相同的.此外，(1)式中P与(2)式中P′的量纲以及(3)式中W与(4)式中W′的量纲也是相同的.

(2)对偶量的值是无关的.例如，设体系A中的电阻R与体系B中的电导G′对偶，当将体系A中的关系式变换到体系B中的对偶关系式时，R将以G′代替，而G′的值与R的值毫无关系.

(3)对偶物理量与对偶关系式之间的变换是以对偶图形与对偶结构为基础的变换.A与B中各对偶元件具有一一对应关系.

4 线性双口网络的对偶等效电路

4.1 线性双口网络的参数

放大器、衰减器、传输线、变压器等大都可视为线性双口网络，其图示如图3.

图3

上图中，U1为输入电压，I1为输入电流，U2为输出电压，I2为输出电流.如果在输入端接一条信号源支路，在输出端接一条负载支路，则U1，I1，U2，I2便都是完全确定的.在输入端的信号源支路中可以列出一个关于U1，I1的方程；在输出端的负载支路中也可以列出一个关于U2，I2的方程.如果不考虑这两个方程，则对于双口网络而言，U1，I1，U2，I2这四个变量中只有两个是独立的.从这四个量中取出两个作为自变量的方法有6种，即C42=6，相应地存在6种基本参数，下面只考虑其中的2种.

(1)微变h参数

在微变h参数中，取I1，U2为自变量，则U1，I2都是I1，U2的函数，即

dU1=u1dU2=u2dI1=i1dI2=i2

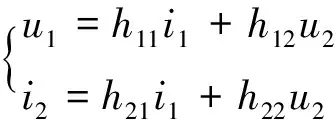
(11)

上式采用矩阵形式表示为

(12)

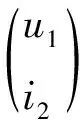
(13)

(2)微变g参数

在h参数中，自变量为I1，U2，因变量为U1，I2.如果将电压与电流互换，则I1，U2与U1，I2互换.与这种互换对应，在微变g参数中，取U1，I2为自变量，而I1，U2为应变量.由类似于(12)式的推导可得

(14)

比较(12)式与(14)式可知，h与g应互为逆矩阵，即

g=h-1h=g-1hg=1

(15)

4.2 两个电路中双口网络的对偶等效电路

如果两个电路A，B中都含有放大器等双口网络，则通常并不能直观地看出这两个电路是否是对偶的.这时，需要将A，B中的双口网络都用等效电路图来代替，然后再讨论A，B是否互对偶，当然首先希望两个双口的等效电路图是互对偶的.这时，两个双口网络等效电路图的对偶尚不是A，B两个完整电路的对偶，而只是A，B中部分电路的对偶.

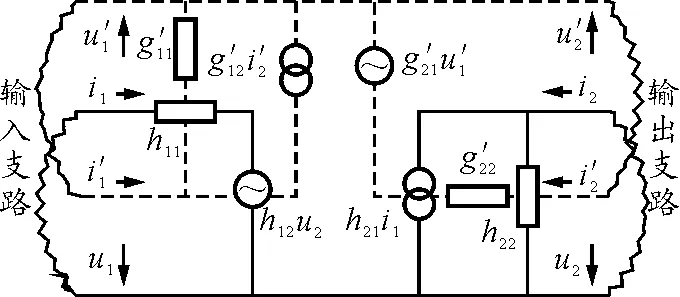
图4

设体系A中的双口网络以h参数描写，则根据(12)式可得其等效电路图如图4中(实线)所示.

为了使体系B中双口网络的等效电路图与体系A中的双口网络的等效电路图对偶，体系B中的双口网络应以g′参数描写.将(14)式中的量改为带撇的量，得

(16)

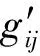
(17)

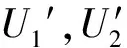
5 交叉桥型双口网络的对偶网络

5.1 无源交叉桥型双口网络

考虑不含信号源的交叉桥型双口网络，如图5所示.

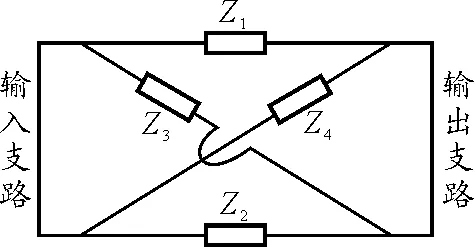
图5

图5中的Z描写支路的阻抗，其对偶支路将以导纳Y′描写.上图可以展开为平面电路图，例如可展开为图6的电路图.

图6

根据平面电路求对偶电路的作图方法便可由上图得到下述对偶电路,如图7所示.

图7

图5与图7互对偶.在图5中，若Z2=0(短路)，则图5化为图8所示的Π型双口网络.

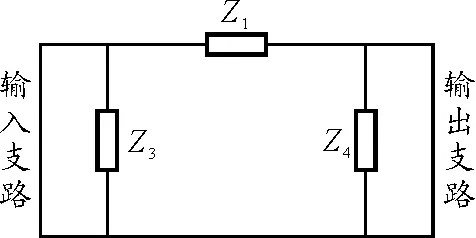
图8

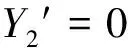
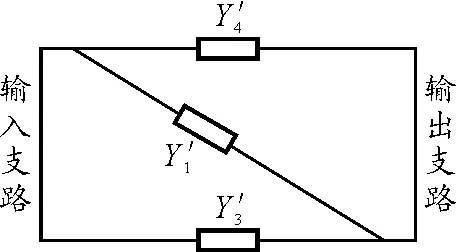
图9

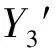
5.2 网孔的选择原则

上面已说到，Π型双口网络的对偶电路可以根据图8得到，也可以根据图6(取Z2=0)得到，两者的差别可归结为对网孔的选择不同.为了能用作图方法得到平面线性网络的对偶网络，对网孔的选择有一个基本原则：网络中的每一条支路只能且必须作为两个网孔的边.在满足选择网孔基本原则的前提下，网孔的选择方法仍可能有多种，从而使得对于同一个线性电路可以得到多种形式的对偶电路，不过这多种形式的对偶电路实际上都是等效的.

参考文献

1 秦曾煌.电工学(第四版).北京：高等教育出版社，1990

2 王惠兰.电路中的对偶原理.物理通报，1994(8)