只有用等效法才行吗

刘金山

(江西省于都中学 江西 赣州 342300)

在重力场和匀强电场所组成的复合场中，某带电小球在竖直面内做圆周(或圆弧)运动，在经过其重力和电场力的合力(也称等效重力)作用线过圆心所对应的圆周上的两个位置时，即所谓的“等效最低点”和“等效最高点”，小球有与之对应的动能最大值和最小值.然而，几乎所有涉及这一复合场的综合题的解答，在所见的各种教辅资料中，都直接运用这一结论，致使一些学生总以为只有用这种等效方法才能解决此类问题.为此，文中对这类问题就等效法之外的求解方法作一探讨.

【例1】如图1所示，在水平方向的匀强电场中，有一质量为m，带正电的小球，用长为L的绝缘细线悬挂于O点，当小球静止时细线与竖直方向夹角为

θ.现给小球一个垂直于悬线的初速度，使小球恰能在竖直平面内做圆周运动， 求：

(1)小球运动过程中的最小速度；

(2)小球在A点的初速度.

图1

方法1：等效重力场法

解析：小球在运动过程中，所受重力和电场力都是恒力，将它们合成等效为一个力F，如图2所示，

则

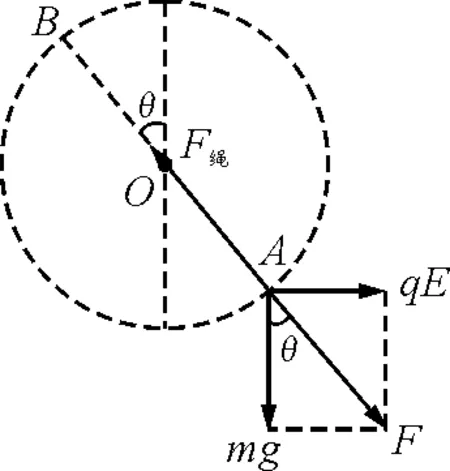
图2

把合力F与重力类比，其等效重力加速度

因此，小球在竖直平面内做圆周运动的等效“最低点”和“最高点”分别为图2中的A点和B点.

(1)小球在B点处的速度最小，依题意有

解得

(2)小球从A点运动到B点的过程中，根据动能定理可列式

解得小球在A点的初速度

方法2：常规解法

解析：如图2所示，因小球在A点是处于静止平衡状态，受竖直方向的重力、水平方向的电场力和沿绳子方向的拉力3个力作用.

(1)因小球在A点获得垂直于悬线的初速度后，恰能在竖直面内做圆周运动，说明小球在运动中速度最小时，绳子张力为零.此位置只能是电场力和重力的合力提供向心力，而这个合力又是恒力，且与小球在A点时的这个合力相同.因此,小球速度最小值的位置必在与A点同一直径圆周的B点上,且满足

而

解得

(2)小球从A点运动到B点的过程中，只有重力和电场力做功，据动能定理可得

其中

解得小球在A点的初速度

(1)小球B的初速度v0大小；

(2)A,B球碰后粘在一起,在半圆轨道上运动的最大速度大小.

图3

方法1：等效重力场法

解析：(1)设小球A，B在c点时的速度为vc，则由平抛运动规律得

代入数据解得

vc=1 m/s

设在B与A碰撞之后，速度为vb,粘在一起由b向c的运动过程中，据动能定理有

代入数据解得

在B与A碰撞过程中，由动量守恒

Mv0=(M+m)vb

所以，B的初速度为

根据等效重力场思想，当A,B运动到所在位置半径与竖直方向成角α=60°时，速度最大，在这过程中由动能定理得

qERsinα-(m+M)gR(1-cosα)=

代入数据解得

vmax=5 m/s

方法2：常规解法

解析：(1)略.

(2)如图4所示，A，B球碰后粘在一起,设在半圆轨道上运动到与bc竖直线的夹角为θ的位置时，两者有最大的共同速度vmax，据动能定理有

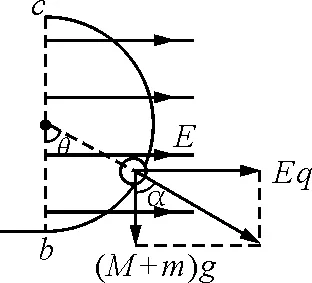
图4

(1)

又因电场力

重力

G=(M+m)g=8 N

且两个力的方向关系满足

得到

α=60°

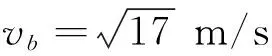
(2)

设θ=30° 时，则

所以，可知当θ=60°时，也就是电场力和重力的合力作用线也过圆心的位置时，A，B两球达到最大速度vmax=5 m/s .

方法3：求导解法

解析：(1)略.

(2)如图4所示，A，B球碰后粘在一起,设在半圆轨道上运动到与bc竖直线的夹角为θ的位置时两者有最大的共同速度vmax，据动能定理有

-(M+m)gR(1-cosθ)+EqRsinθ=

(3)

代入对应的已知量得到数值方程

(4)

据式(2)，令

对y求解一阶导数得

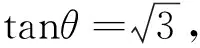
所以当θ=60°时，y有最大值

ymax=25

可得

vmax=5 m/s

结语：由上可见，等效法固然是一种不错的方法，但是并非非它莫属.在当今倡导教学应注重过程的理念下，对一个问题用不同方法进行探究，这是笔者写下本文的初衷.