模糊PD控制器在电液伺服阀控制系统中的应用

赵振飞，陈奎生，邓江洪

（武汉科技大学机械自动化学院，湖北武汉，430081）

伺服阀是液压伺服系统的核心部件，其控制精度直接影响到整个系统的性能。PD控制方法由于算法简单、可靠性高而被广泛应用于伺服控制系统中，但其动态跟随性能较差，很难满足高精度随动控制系统的要求。因此，本文将模糊控制原理应用于电液伺服阀控制系统中，设计一个模糊PD控制器，采用AMESim软件建立伺服阀的仿真模型，采用Simulink软件建立模糊PD控制器仿真模型，通过AMESim／Simulink联合仿真对伺服阀的性能进行分析，并与常规PD控制下的伺服阀性能进行比较。

1 电液伺服阀结构与工作原理

图1 电液伺服阀结构简图Fig.1 Structure diagram of electric－hydraulic servo valve

先导式电液伺服阀由小流量的先导阀、功率滑阀、传感器和控制器组成，如图1所示。通过控制先导阀的流量来驱动功率滑阀的移动，通过传感器将位移信号反馈给控制器以形成闭环控制，从而精确地控制输出流量。

2 伺服阀控制方式选择

2.1 PD控制

PD校正又称为比例－微分校正，其传递函数为：

式中：Kp为比例系数；Kd为微分系数。由于微分控制对误差信号的变化趋势具有“预测”的能力，因此PD校正能在误差信号变化之前给出校正信号，以防止系统出现过大的偏离和振荡，从而有效地改善系统的动态性能[1]。

2.2 模糊PD控制

模糊控制和精确控制一样，是一种闭环控制系统，其不同之处在于，模糊控制器中采用的模糊量与模糊推理、模糊量与精确量之间的转换以及模糊推理规则均由专家经验予以确定。模糊控制的优点是不要求掌握受控对象的精确数学模型，而是根据人工控制规则组织控制决策表，然后由该表决定控制量的大小[2]。模糊PD控制的具体方法是，将操作人员通过长期实践积累的经验用控制规则模糊化，然后运用模糊逻辑推理对PD的比例系数、微分系数进行实时修正，影响PD控制器的输出，进而实现系统的最优控制，其原理如图2所示。

图2 模糊PD控制原理图Fig.2 Fuzzy PD control diagram

本系统以伺服阀阀芯的位移为控制对象，以目标位移和实际位移的偏差e以及偏差的变化ec作为输入量，以PD控制器的比例系数Kp和微分系数Kd作为输出量，并通过模糊化将其映射到各自的论域E，EC，KP，KD内。E、EC、KP和KD的模糊集为｛NL，NM，NS，O，PS，PM，PL｝；E和EC的论域为｛－3，－2，－1，0，1，2，3｝；KP和KD的论域为｛－0.03，－0.02，－0.01，0，0.01，0.02，0.03｝。在模糊子集为“负大（NL）”和“正大（PL）”时，选择正态分布的模糊隶属度函数；在其他模糊子集时，选择三角形隶属度函数。各变量的隶属度图形如图3和图4所示。

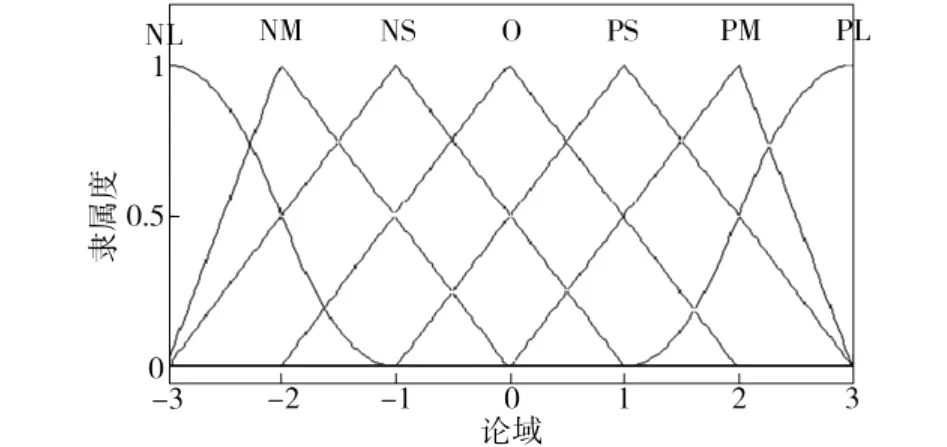
图3 E和EC的隶属度Fig.3 Membership degree of E and EC

图4 KP和KD的隶属度Fig.4 Membership degree of KP and KD

模糊PD控制器选取控制变量的原则是：当误差大或较大时，选取控制变量主要考虑尽快消除误差；当误差较小时，选取控制变量主要考虑系统的稳定性，防止系统超调。Kp的作用是响应速度快，调节精度高，但Kp取值过大会导致超调以及系统的稳定性下降；Kd的作用是改善系统的动态特性，控制偏差，对偏差进行提前预报[3]。通过动态改变Kp和Kd的值来修改控制参数，优化控制性能。根据这个原则可得到相应的模糊规则，如表1和表2所示。

表1 K P的模糊规则Table 1 Fuzzy rules of KP

表2 KD的模糊规则Table 2 Fuzzy rules of KD

一般情况下，模糊PD控制器对参数Kp和Kd采用增量式在线调整方法，此时

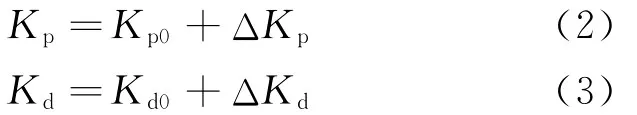
式中：Kp0和Kd0为控制器的初值；ΔKp和ΔKd为模糊推理的结果。

3 仿真模型的建立

AMESim仿真软件提供了一个完善的时域仿真建模环境，用户可以通过使用已有模型或建立新的子模型元件，来构建优化设计所需的实际原型。在AMESim中专门为液压系统建立了一个标准仿真模型库以及液压基本元件设计HCD库，方便用户快捷、有效地建立液压系统和液压元件模型[4－5]。Simulink是MATLAB中的一种可视化仿真工具，被广泛应用于线性系统、非线性系统、数字控制及数字信号处理的建模和仿真中。利用AMESim对Simulink的接口技术将两个优秀的专业仿真工具联合起来使用，既能发挥AMESim突出的液压系统仿真功能，又能发挥MATLAB／Simulink强大的数值处理能力，取得良好的互补效果[6]。

本文采用AMESim建立先导式电液伺服阀仿真模型（见图5），其中先导阀模型采用AMESim液压库中的标准模型，功率滑阀模型根据实际物理模型通过HCD库中的液压元件搭建而成[7]。

图5 先导式电液伺服阀仿真模型Fig.5 Simulation model of pilot electro－hydraulic servo valve

根据PD控制和模糊PD控制原理在Simulink中建立PD控制器和模糊PD控制器的仿真模型如图6和图7所示。模糊PD控制系统中，模糊控制器采用Mamdani推理方法进行模糊推理，计算出输入论域上每点对应的模糊控制量，再通过重心法解模糊，然后根据具体的输入变量产生输出变量。另外，伺服阀AMESim模型通过S－Function接口导入到Simulink模型当中。

图6 PD控制Simulink仿真模型Fig.6 Simulink model of PD control

图7 模糊PD控制Simulink仿真模型Fig.7 Simulink model of fuzzy PD control

4 仿真试验与结果分析

根据图1所示电液伺服阀的实际数据来设置仿真模型的各项参数。先导阀控制压力为21 MPa，控制流量为2.5 L／min，频率为80 Hz。功率滑阀额定压力为7 MPa，阀芯直径为20 mm，质量为0.5 kg，控制阀芯行程为1.6 mm。阀芯的黏性摩擦系数为0.05 N·s／m，瞬态液动力阻尼系数为2.19 N·s／m，通过质量模块进行模拟。阀口的稳态液动力通过AMESim的阀芯模块根据开口度的大小自动计算出来。

图8为仿真试验得到的电液伺服阀在PD控制和模糊PD控制作用下的阶跃信号响应曲线。从图8中可以看出，与PD控制相比，在模糊PD控制作用下伺服阀阶跃信号响应曲线的超调量明显减小，响应过程也较平稳。模糊PD控制提高了整个系统的可靠性和抗干扰能力，系统的鲁棒性有所增强，伺服阀的性能得到改善。

图8 电液伺服阀阶跃信号响应曲线Fig.8 Step representation signal response curve of electrohydraulic servo valve

5 结语

模糊PD控制器在执行过程中能够实时修正PD控制参数，从而提高了系统控制精度，有效地改善了电液伺服阀的性能。采用AMESim软件能够方便快捷地建立伺服阀仿真模型，而AMES－im／Simulink联合仿真则综合利用了两个仿真软件的优势，是一种效果良好且不是很复杂的仿真途径。

[1] 李建勇.机电控制工程基础[M].北京：中央广播电视大学出版社，2008：172－173.

[2] 孙惠杰.转阀式直接驱动伺服阀的参数自调整模糊PID控制[J].微电子学与计算机，2008，25（9）：141－143.

[3] 杨永，张根宝.模糊PD控制在伺服系统中的应用[J].陕西科技大学学报，2009，27（4）：117－120.

[4] 余佑官，龚国芳，胡国良.AMESim仿真技术及其在液压系统中的应用[J].液压气动与密封，2005（3）：28－30.

[5] 罗春雷，李雄，邓强泉，等.利用AMESim的密炼机上顶栓液压传动系统动态分析[J].现代制造工程，2010（9）：135－138.

[6] 李谨，邓卫华.AMESim与MATLAB／Simulink联合仿真技术及应用[J].情报指挥控制系统与仿真技术，2004，26（5）：61－64.

[7] 刘小初，叶正茂，韩俊伟，等.基于AMESim软件的三级电液伺服阀建模与仿真[J].机床与液压，2008，36（11）：630－631.