高考题中平抛运动最值问题的探秘与赏析

陈晓东

(江苏省石庄高级中学 江苏 南通 226531)

笔者仔细分析了2010各地高考题，发觉江苏、重庆、浙江三地都在计算题中以平抛运动为载体，考查了求最值的问题，应该说试题的综合性较强、灵活性较大，凸显了中学物理教学大纲所提出的“运用数学解决物理问题的能力”．乍一看，给人耳目一新的感觉，但细细回味，不难发现这些题的“原型”其实都很熟悉，而且这一“源”题都做过、考过．无非是用新瓶包装了一下，里面装的还是陈酒．本文对此进行了归纳整理，与大家探讨．

【例1】(2010年高考江苏物理卷第14题)在娱乐节目中，选手需要借助悬挂在高处的绳飞越到水面的浮台上，小明和小阳观看后对此进行了讨论．如图1所示，他们将选手简化为质量m=60 kg的质点， 选手抓住绳由静止开始摆动，此时绳与竖直方向夹角α=30°，绳的悬挂点O距水面的高度为H=3 m.不考虑空气阻力和绳的质量，浮台露出水面的高度不计，水足够深．取重力加速度g=10 m/s2，sin53°=0.8，cos53°=0.6.

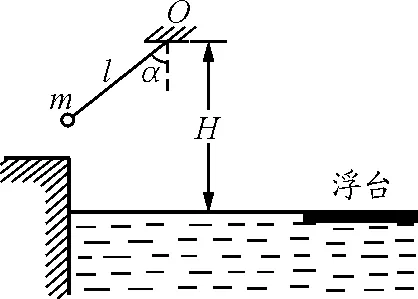
图1

(1)求选手摆到最低点时对绳拉力的大小F；

(2)若绳长l=2 m,选手摆到最高点时松手落入水中．设水对选手的平均浮力f1=800 N，平均阻力f2=700 N，求选手落入水中的深度d；

(3)若选手摆到最低点时松手， 小明认为绳越长，在浮台上的落点距岸边越远；小阳认为绳越短，落点距岸边越远，请通过推算说明你的观点．

解析：(1)由机械能守恒

(1)

质点作圆周运动，由向心力公式，有

解得

F′=(3-2cosα)mg

人对绳的拉力

F=F′

则

F=1 080 N

(2)由动能定理

mg(H-lcosα+d)-(f1+f2)d=0

解得d=1.2 m.

(3)选手从最低点开始做平抛运动x=vt

且由式(1)，解得

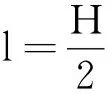
因此，两人的看法均不正确.当绳长越接近1.5 m时，落点距岸边越远.

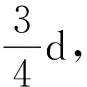
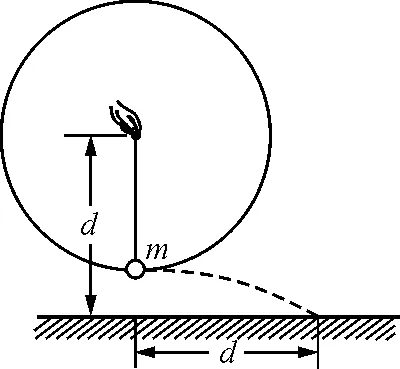
图2

(1)求绳断时球的速度大小v1和球落地时的速度大小v2．

(2)轻绳能承受的最大拉力多大？

(3)改变绳长，使球重复上述运动，若绳仍在球运动到最低点时断掉，要使球抛出的水平距离最大，绳长应是多少？最大水平距离为多少？

由机械能守恒定律，有

得

(2)设绳能承受的最大拉力大小为T，这也是球受到绳的最大拉力大小．

得

(3)设绳长为l，绳断时球的速度大小为v3，绳承受的最大拉力不变，有

得

绳断后球做平抛运动，竖直位移为d-l，水平位移为x，时间为t1,有

得

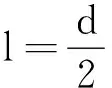
【例3】(2010年高考浙江物理卷第22题)在一次国际城市运动会中，要求运动员从高为H的平台上A点由静止出发，沿着动摩擦因数为μ的滑道向下运动到B点后水平滑出，最后落在水池中．设滑道的水平距离为L，B点的高度h可由运动员自由调节(取g=10 m/s2)．求：

(1)运动员到达B点的速度与高度h的关系；

(2)运动员要达到最大水平运动距离，B点的高度h应调为多大？对应的最大水平距离smax为多少？

(3)若图3中H=4 m，L=5 m，动摩擦因数μ=0.2，问水平运动距离要达到7 m，h值应为多少？

图3

解析：(1)由A运动到B过程，有

(2)平抛运动过程中

解得

smax=L+H-μL

h2-3h+1=0

解得

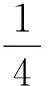
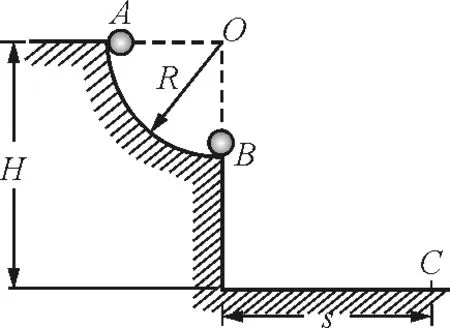
图4

(1)小球刚运动到B点时，对轨道的压力多大?

(2)小球落地点C与B的水平距离s为多少?

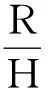
解析:(1) 小球沿圆弧做圆周运动,在B点由牛顿第二定律，有

从A到B，以B点为零势能点，由机械能守恒定律,有

由以上两式得NB=3mg，由牛顿第三定律，得小球对轨道的压力为3mg.

(2)小球离开B点后做平抛运动,抛出点高为H-R，有

s=vBt

解得

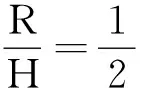
smax=H

评析：以上列举的3道高考题都很新颖，其中在知识方面综合考查了牛顿运动定律、平抛运动、圆周运动、匀变速直线运动、机械能守恒定律、动能定理等大纲中明确要求学生理解并掌握的知识点；能力方面考查了求解平抛运动中最大水平分位移的问题；在具体求解时，源题与3道高考题都用到了高中数学中所学的极值定理．比较起来，无论是知识上还是能力上，几道高考题与源题都有惊人的相似之处，都是在源题的基础上换了一下情境，其实大多数题追根溯源，都能找到它的“活水源头”.作为一线教师，在平时除了要把题目讲精、讲透外，还得注重适当的拓展延伸，有效进行知识的迁移和应用，着力培养学生的发散性思维能力，以不变应万变，在知识、方法和能力等方面全面贯彻新课程理念．