浅谈平面振子的阻尼运动

肖 筱 陶寅莹 李 庆

(电子科技大学英才实验学院 四川 成都 611731)

滕保华

(电子科技大学物理电子学院 四川 成都 610054)

大学物理中对通常的阻尼振动和平面振子已经有了很多研究[1～4]，但阻尼振动的研究主要是基于一维运动，而平面振子的研究则是基于无阻尼的运动．本文将研究阻尼情况下的平面振子运动,并讨论阻尼系数对其运动轨迹的影响．

图1 平面振子示意图

设振子系统的一端固定在水平面上O点，另一端系一质量为m的质点， 弹簧的劲度系数和原长分别为κ和l．若质点受一阻力f=-αv(α为阻尼系数)，则在极坐标下，振子的运动方程可以写成

(1)

和

(2)

由(2)式直接得到振子系统的角动量为

(3)

这里J0是振子的初始角动量．显然，在有阻尼情况下振子系统的角动量是随时间t指数衰减的．于是任意时刻振子的位置可由下述微分方程和积分方程确定

(4)

(5)

利用Mathcad[5]数值计算可以得到在一定参数和初始条件下平面振子阻尼运动的轨迹，如图2所示．图中初始条件设置为：振子初始伸长量为1 m，初速度大小为2.45 m/s，其方向与极轴OA夹角为42.8°．可以看出，阻尼系数α为零时振子运动轨迹呈规则的花瓣状，并且位于一个内切圆和一个外接圆之间[4]．而阻尼系数α不为零时，振子的运动轨迹与上明显不同，即阻尼系数α的大小敏感地影响振子运动轨迹的长短和形状．随着阻尼系数α的增大，一方面阻尼因素将导致平面振子的运动轨迹快速变短；另一方面阻尼还将使其运动轨迹的形状明显偏离花瓣状，并在一定情况下有阻尼的平面振子运动轨迹会部分落入到无阻尼振子运动轨迹的内切圆中．

图2 无阻尼和有阻尼时的平面振子轨迹,这里参数分别为：m=1,α=0.2，κ=2，l=2,J0=5(均为国际单位)

为了说明阻尼系数α不为零时平面振子运动轨迹部分落入内切圆中的轨迹特点，可以分析平面振子的径向速度和横向速度.在极坐标下振子的径向速度和横向速度分别由下式决定

利用Mathcad数值计算，可以得到与图2相同的参数下有阻尼和无阻尼时振子径向速度vi(t)和横向速度vj(t)，分别如图3(a)和3(b)所示．

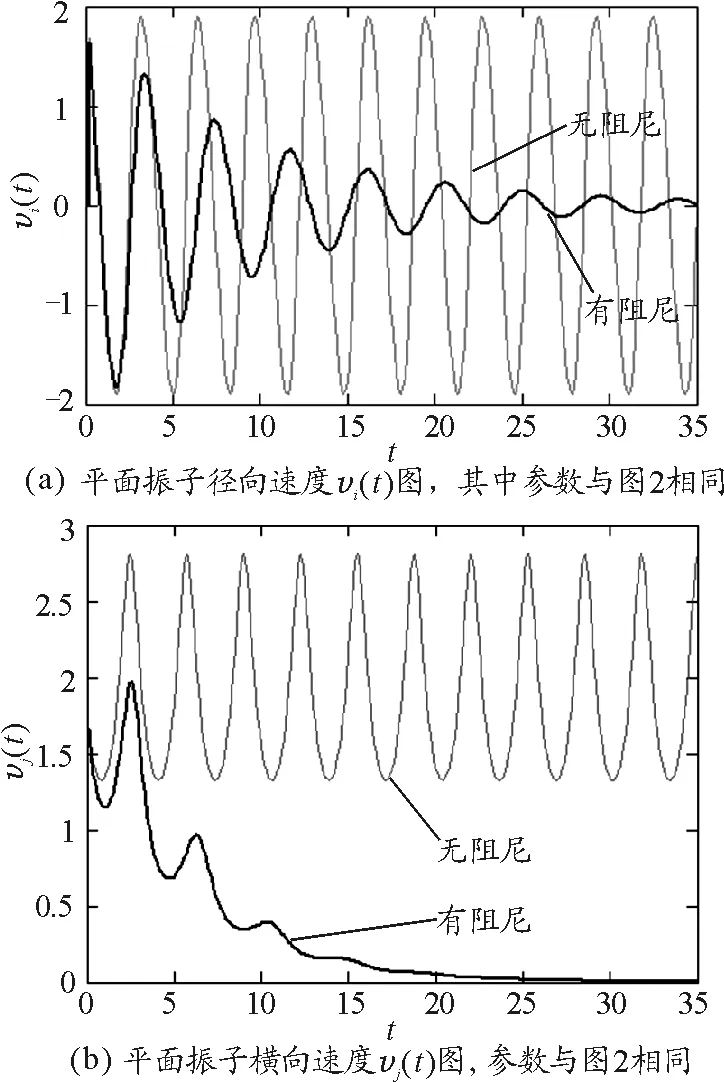
图3

可以看出，无阻尼时振子的径向速度随时间简谐变化，但横向速度是平移到坐标轴上方某正数附近非简谐的周期变化．阻尼系数α不为零时,振子的径向速度和横向速度都是随时间衰减的，并且径向速度与一维阻尼振子的速度衰减趋势完全相似，但是此时横向速度却是从坐标轴上方某正数附近一直振荡衰减到零．也就是说，此时振子横向速度的衰减变化趋势与无阻尼时振子横向速度的变化趋势大相径庭．由此可以发现，阻尼系数α不为零时平面振子轨迹之所以部分落入无阻尼时的内切圆内，是因为其横向速度相比无阻尼时不协调地衰减，导致平面振子所需的向心力相比无阻尼时相应减小，在弹力的作用下，最终使得平面振子在运动过程中部分落入无阻尼时的内切圆内．

综上所述，本文通过建立平面振子在有阻尼情况下的动力学方程，利用Mathcad数值求解了一定条件下平面振子的运动轨迹，并分析了阻尼因素对其运动轨迹的影响．同时指出，有阻尼时平面振子横向速度的迅速衰减特征是导致有阻尼时运动轨迹部分落入无阻尼时轨迹内切圆的主要原因．

参考文献

1 周衍柏.理论力学教程.北京:高等教育出版社,1979.69

2 (美)H·戈德斯坦著.汤家镛，陈为恂译.经典力学.北京:科学出版社,1981.71～87

3 赵凯华.新概念物理教程·力学.北京:高等教育出版社,2004.329

4 Scheck F. Mechanics: From Newton′s Laws to Deterministic Chaos (Berlin: Springer) 2004.47～49

5 郑桂水.Mathcad2000实用教程.北京:国防工业出版社,2000.172～176