基于渐进结构优化法的拱坝结构曲线函数优化

左中杰, 干 泉, 王运兴, 翟传明, 张华栋

( 1.中电投工程研究检测评定中心， 北京 100840； 2.中机三勘岩土工程有限公司， 湖北 武汉 430030；3.中建(北京)国际设计顾问有限公司， 北京 100013)

人类修建拱坝有着悠久的历史。近年来世界各国着重建设各种体形的拱坝，然而拱坝建设是一项大型的水利工程项目，投资巨大，耗时较长，为了减少拱坝建设费用，缩短建设周期，开展拱坝的优化研究就变得具有现实意义。

尽管拱坝有着安全度高、承载能力强等诸多优点，但拱坝的开裂现象几乎和拱坝自身历史一样久远。国内外由于拱坝开裂而失事或影响运行的事例不胜枚举。表面性的裂缝不会对大坝的安全性能造成影响，但结构性裂缝，对坝的使用和工程整体性能造成不可估量的破坏。于是对坝体的结构优化应最大程度地降低裂缝发生的可能性。

拱坝优化设计的主要方法是调整初始模型中的各个参数，使拱坝各个截面的受力趋于合理。当前，对拱坝的优化设计多变量、非线性等问题。以往的设计方法多采用准则法和数学规划法，目前多采用有限单元法，以及由此发展的拓扑优化分析方法。

准则法主要有强度准则、刚度准则、以及能量准则等。具体还可以分为满应力准则和满应能准则。

数学规划法分为线性规划和非线性规化法两种。拱坝优化属于非线性规划，详细可分为：列线性规划法(SLP)；罚函数法；序列二次规划法(SQP)三种类型。

有限单元法目前已发展成为拱坝体型优化的常用方法。可以综合考虑地基、地质、地形对拱坝的影响计算坝体的变形和应力，还可以模拟材料间复杂的本构关系，以达到精确近似工程设计的目的。通过市场上大型有限元软件进行快速求解，并利用软件的高级功能对其曲线模拟等，既提高了优化效率，又能根据设计要求对拱进行修正。

拓扑优化是最近发展起来的一种优化方法，其中主要有变密度法、均匀法等思想。主要是对拱坝以及基岩进行简化模拟，然后对拱坝给定一个初始体形，设定要优化的变量、目标函数、约束条件，进行拓扑优化设计。目前常用的有限元软件有NSYS、MSCMARC等，都是比较优秀的计算工具。

我国在拱坝建设取得显著进展：拱坝优化不再以经济指标为单目标进行优化而是考虑应力水平、失效概率、高应力区范围等安全性指标的多目标优化；拱坝优化已由早期的线性优化已转变到非线性分析、混合线性优化及拓扑优化等。

结构拓扑优化的主要研究对象是连续体结构。连续体结构的拓扑优化设计出现了不同的求解体系。国内学者主要主要集中在局部应力约束下的强度拓扑优化设计，而国外研究人员多集中研究全局体积约束下的拓扑优化。

1992年，Xie和Steven提出了渐进结构优化算法，主要原理在优化区域以一定的删除准则逐步删除低应力单元，使得结构在满足一定的约束条件下，应力状态和目标函数达到最优。该法具有删除单元后无法恢复的缺点；因此，Querin和Steven等对传统的渐进结构优化算法进行了改进，在删除单元后应力较高的区域增加单元，使得应力集中现象降低；Kim和Kwak对空间优化问题进行了深入的探讨；Huang和Xie提出基于双方向渐进结构优化的研究方法，对周期结构和具有一种或多种材料的结构的拓扑优化问题进行了拓展。

1 渐进结构优化方法基本思想和优化准则

1.1 渐进结构优化(ESO)方法

1993年，谢忆民和Steven提出了渐进结构优化方法(Evolutionary Strueture Optimization，简称ESO法)。认为在设计区域内，结构上不起作用的材料，即那些低应力或低应变能密度的材料是低效的，是可以去除的。之后荣见华将这种优化方法应用于包含应力、位移(刚度)、动力学约束和临界应力领域，取得了很好的成果。

渐进结构优化方法的基本原理是逐步删除最不起作用的材料，剩余结构逐步达到最优解。在优化迭代中，该方法采用对存在的材料单元，其材料数编号为非零常数，而对不存在的材料单元数编号为零(或使得模型乘以接近为零的系数)。该方法容易利用现有有限元分析软件，通过多次迭代得以实现其所表现的拓扑优化计算，因此该方法具有较好的通用性。

1.2 基于单元生死功能的优化准则

对于静力设计问题，ESO方法通常采用基于应力准则的优化方法。对于各向同性材料，VonMises应力是目前最为常用的应用准则。

对于平面应力问题VonMises应力σvm定义为：

(1)

式中σx和σy分别是x和y方向的正应力；τxy为剪应力

(2)

式中，RRi为当前的材料删除率；一般初始删除率RR0是人为取定值。在当前子迭代中采用相同的RRi值，反复进行子迭代运算，同时删除满足条件的单元，直到进入应力或体积稳定状态，表明在当前迭代步中，已经不存在满足条件需要删除的单元。在下一次迭代运算中，引进一个进化率ER，这样删除率被改变，即：

RRi+1=RRi+ER，i=0,1,2…

(3)

在改进的删除率下，又有一些满足删除条件的单元，执行新一次单元删除循环，直到达到没有单元被删除，停止迭代达到新的稳态，从而获得一个最佳结构。理想的最终结构变成一个满应力的设计即结构的每一点的材料应力达到它的满强度。

1.3 有限元分析基本流程

(1)选择准备设计区域，用有限元网格离散全部区域，将准备优化的区域定义不同的单元类型；

(2)对结构施加荷载和边界约束，选择静力分析的方法进行静力分析；

(4)将以上步骤重复进行，直至(2)式无法满足且收敛到设计要求为止。此时，对应于RRi的结构已达到稳定状态。为使优化继续进行，引进进化率ER，从而下一稳定状态的删除率修改为式(3)；

(5)重复步骤2～4步直至结构满足要求为止。

1.4 拓扑优化软件实现

本文基于ESO法，利用ANSYS的单元生死对厚拱平面进行拓扑优化设计，采用APDL语言二次开发，编制循环程序设定删除率，将设计区域内应力相对低的单元或低应变能密度的单元“杀死”。逐步“杀死”低效单元，最终得到满足应力要求及最有目标的结构模型。

2 厚拱拱坝结构的拓扑优化计算

2.1 拱坝设计资料介绍

本文在对某二维厚拱拱坝进行拓扑优化应用的基础上，其新意在于二次拱结构形式的分析。基本设计资料为：拱坝形式为单圆心拱坝，如图1所示，圆心角θ=80°，外径R=450 m，内径r=350 m，拱厚T=100 m。厚拱判断条件：D=0.5(R+r)，T/D=0.25，满足厚拱(T/D=0.2～0.3)要求。坝体作为均质材料考虑，弹性模量Ec= 30.0 G Pa，泊松比取μc= 0.3，拱坝承受均布水压力为350 kN/m2。

图1 厚拱拱坝结构初始尺寸

2.2 拱坝结构拓扑优化计算模型

本例中厚拱结构采用ANSYS单元库中8节点平面单元plane 82进行平面应力分析，将拱坝结构离散，共划分10509个节点和5122个单元，其计算模型如图2所示。

图2 厚拱拱坝结构有限元计算模型

2.3 拱坝结构拓扑优化结果分析

基于Von Mises屈服准则确定的Von Mises Stress(等效应力)可以快速的确定模型中的最危险区域。

本文渐进优化方法以单元的等效应力为依据，对满足删除条件的单元进行选择、删除。对拱坝结构初始模型进行加载及施加位移约束后，得到相应的等效应力、主应力计算结果见图3～5，其中图3为初始化模型后的单元等效应力等值图，图4为其结构单元第一主应力等值图，图5为初始化模型的节点第一主应力。通过对拱坝初始模型设定删除率，取RRi=10%，ER=10%，经过40次迭代计算后，结构单元删除为零，得到迭代优化40次后的拓扑优化结果云图，此时拱坝结构的体积为满足删除率的最小体积。其计算结果如图6～8所示，文中云图结果单位为kPa。

图3 拱坝模型初始化单元等效应力云图

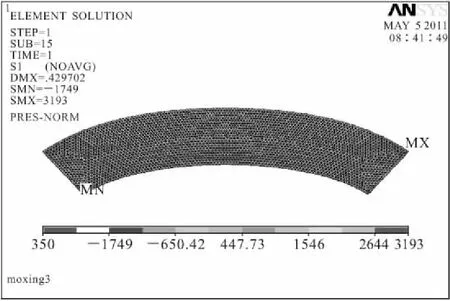
图4 拱坝模型初始化单元第一主应力云图

图5 拱坝模型初始化节点第一主应力云图

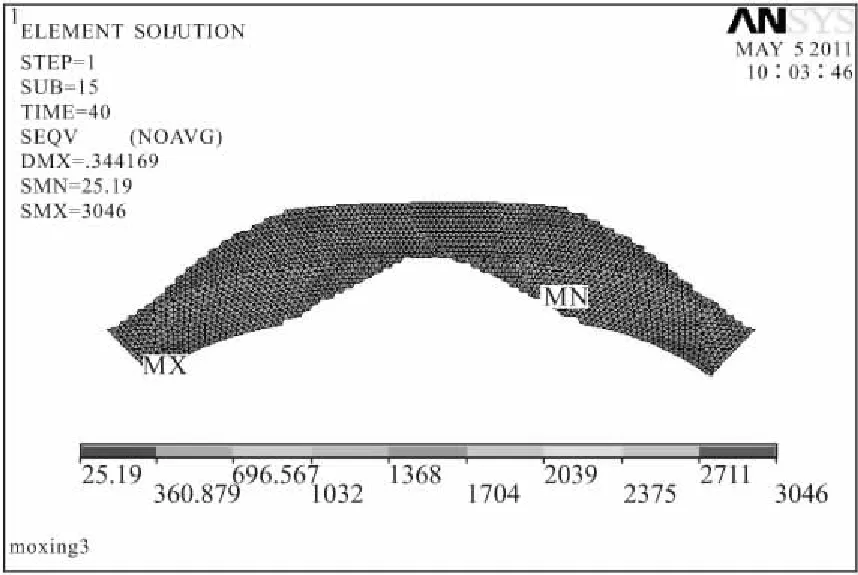
图6 迭代40次单元等效应力云图

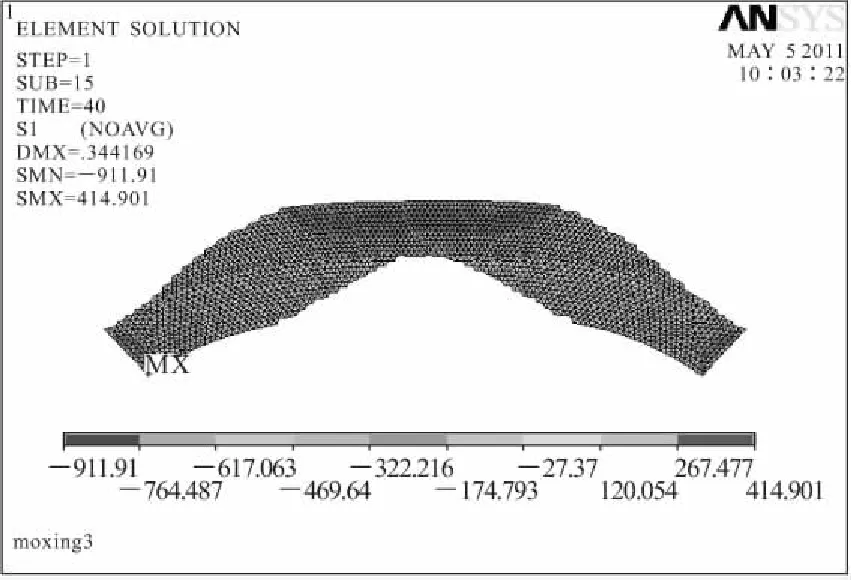
图7 迭代40次单元第一主应力云图

图8 迭代40次节点第一主应力云图

由上述云图可以得出，拱坝在进行迭代的过程中无论是单元等效应力，还是单元和节点的最大主拉应力都得到大幅降低，使得拱坝最大拉应力处于混凝土的容许拉应力状态，结构趋于安全。另外还可以得出水平拱圈各区域主拉应力的大致分布情况，以及整体危险点位置。拱圈初始模型中发生在基岩相接触的角点处的主拉应力最大值，在优化过程中混凝土的最大拉应力σ1<1.4 MPa，整个水平拱圈较安全，优化结果达到了预期的目标。

从图9～11可以计算出，拱坝结构优化过程中，结构体积减少33%，单元等效应力最大值约减小50%，节点第一主应力最大值减小约为92%。

图9 拱坝结构体积随迭代次数变化曲线

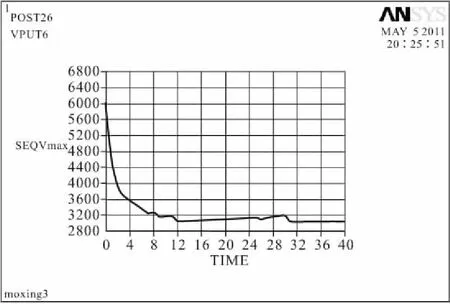
图10 单元等效应力最大值随迭代次数变化曲线

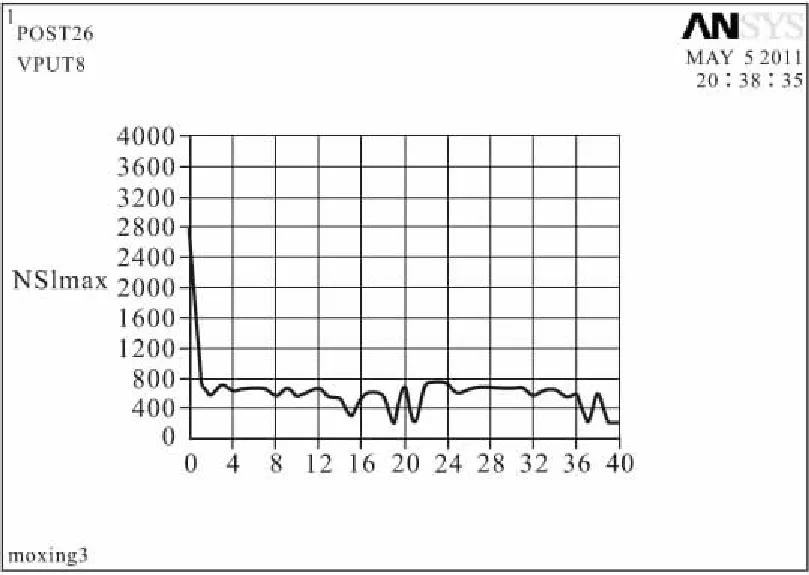
图11 节点第一主应最大值随迭代次数变化曲线

2.4 拱坝结构二次拱拟合分析

为了验证拱坝结构拓扑优化后，其内部可能存在的二次拱，为此对优化后的结构进行曲线拟合，得出二次拱结构的曲线。现利用Origin对拱坝拓扑优化后结构上的数据进行曲线拟合，其拱坝上下游曲线方程分别为：

y=4.11×10-16x-2.35×10-3x2+454.68

(4)

y=1.11×1016x-2.48×10-3x2+385.71

(5)

上下游拓扑优化曲线与拟合曲线如图12所示，图中纵、横坐标表示距离，单位为m。

图12 拓扑优化后二次拱曲线

通过拟合的两条抛物线建立拓扑优化后的二次拱模型，并对其加载及施加位移约束，分析其节点第一主应力及第三主应力，如图13～14所示。

图13 拟合结构第一主应力云图

图14 拟合结构第三主应力云图

由云图中数据可知，第一主应力的最大值小于坝体材料的抗拉强度(1.4 MPa)，第三主应力最大值为3.045 MPa，也小于14 MPa，因此该拟合二次拱坝的主压应力、主拉应力满足材料强度要求。由此可以得出在已经开裂的拱坝中存在一定形式的二次拱满足不使混凝土开裂的要求。

3 其他形式的拱坝合理受力轴线分析

上述拓扑优化结果分析得出，单心圆拱坝的二次拱的结构形式呈抛物线，本节在拓扑优化的基础上，分析厚拱拱坝结构的合理受力形式，采用与单心圆拱坝相同的工程背景，重点分析三心圆形式，对类似拱坝结构的设计具有借鉴和指导作用。

3.1 三心圆拱坝结构受力分析及结构优化

如图15所示，三心圆的净宽为单心圆的弦长长度，净高取250 m。该拱坝承受与单心圆相同荷载，利用Ansys有限元计算，计算分析结果见图16。

图15 三心圆拱坝结构形式

图16 三心圆拱应力分析及优化结构的应力

云图中三心圆拱初始模型的节点第一主应力最大值小于1.4 MPa。且经结构优化后，结构体积减小23.8%，且主拉应力较小，不会造成拱坝产生结构性裂缝，满足结构安全。这说明了三心圆受力轴线也是拱坝工程设计中需要考虑的结构形式。

4 结 语

本文主要借助ESO法的基本思想以及对ANSYS单元生死功能的二次开发，应用APDL语言编制循环程序设定删除率，通过对单心圆厚拱拱坝结构的拓扑优化，优化结果满足安全要求，实现了材料的有效利用。从而表明将拓扑优化方法用于拱坝的体形优化设计中是可行的。同时验证了拱坝结构材料开裂后二次拱的存在，即在原始模型中存在一个二次拱使得在拱坝高应力区域得到分散，内力重分布，且二次拱的结构形式多为抛物线。尝试分析了三心圆拱坝的受力状况。

[1] Xie Y M, Steven G P. A simple evolutionary procedure for structural optimization[J]. Computers & Structures， 1993, 49(5): 885-896.

[2] Huang X, Xie Y M. Optimal design of periodic structures using evolutionary topology optimization[J]. Structural & Multidisciplinary Optimization, 2008, 36(6): 597-606.

[3] Huang X, Xie Y M. Bi-directional evolutionary topology optimization of continuum structures with one or multiple materials[J].Computational Mechanics, 2009, 43(3):393-401.

[4] Bendsoe M P. Scale effects in the optimal design of a microstructuredmedium against buckling[J]. Int J Solids and Structures, 1990, (26): 725-741.

[5] 周春平，常锦昕. 基于单元生死功能的转向架构架拓扑优化设计[J]. 计算机仿真, 2010, 27(5):267-271.

[6] 穆春燕. 拓扑优化理论及其在拱坝优化设计中的应用[D]. 南京：河海大学，2006.

[7] 郭中泽. 基于单元特性改变的渐进结构拓扑优化方法及应用研究[D].北京：中国工程物理研究所，2006.

[8] 汝乃毕. 拱坝开裂的历史经验[J].水利学报，1990, (9)：17-25.

[9] 武 亮,叶文明,何仕华. 基于ANSYS的拱坝等效应力分析[J]. 水利水电技术， 2006, 37(9)：27-29.

[10] 高 健.拱坝开裂约束下体形优化设计研究[J].河海大学学报(自然科学版)，2006, 34(5)：526-529.

[11] 董桂西,王藏柱.结构优化设计的现状及展望[J].电力情报, 2000，(1):5-7.