基于系统动力学的多方安全监管博弈

贾 璐， 蔡建国

(1.华中科技大学 土木工程与力学学院， 湖北 武汉 430074;2.西安建筑科技大学 土木工程学院， 陕西 西安 710055)

进入21世纪以来，我国经济建设持续高速发展，人民生活水平稳步提高。作为国家支柱性产业之一的建筑业，受固定资产投资的拉动和城镇化进程加速的影响，近10年来也经历了长足的进步，取得了令人瞩目的成绩[1]。然而，伴随着建筑业的高速发展，工程建设过程中的安全问题却总像是达摩克利斯之剑，高悬在政府相关职能部门和广大建筑业从业人员的头上，每年均有不同程度的重特大事故发生，这使得建筑业成为仅次于道路交通、矿山工程的第三大危险行业[2]。

工程建设过程中的安全监管属于社会性管制的范畴，其目的是希望相关安全监管部门对工程各参建方的具体行为是否符合相关法律、法规和工程建设标准的要求进行有效的控制，以期达到保障工程顺利进行，降低工程安全风险，较少事故数量和死伤人员数量的目的。鉴于安全监管过程中有监管者与被监管者两个参与方，其在工程监管过程中存在有监管博弈的问题。

近年来，针对我国工程建设过程中重特大事故屡有发生，伤亡人数较大的现状，不少学者也开始采用博弈理论研究工程建设过程中的安全监管问题，为减少建筑安全事故的发生，保障中国经济社会和谐发展献言献策。袁海林等分析了政府与企业、企业与企业间的博弈过程，并指出了企业实施建筑安全控制动力不足的原因并提出政策建议[3]。曹冬平等建立了一个以建设行政监管部门和建筑企业为参与者的安全监管博弈模型，从博弈双方的角度分析了导致我国建筑生产安全问题的主要原因，并提出了部分政策建议[4]。张玉娟等针对中国建筑业安全事故频繁且对建筑业造成严重不良影响的现状，分别建立并分析了市场准入和施工安全管制博弈模型，提出了一些降低安全事故发生率的解决办法[5]。黄海斌等通过建立博弈模型对建筑安全检查进行了定量分析，并对安全检查部门和被检查单位的具体行为作了详细的阐述[6]。肖兴志等基于政府、建筑企业、建筑工人三方博弈主体的利益考虑，就整个安全链条分别建立博弈模型，分析安全事放发生的原因，并提出了相应政策建议[2]。即有文献多采用完全信息静态博弈的方式，博弈参与方均局限于两个，而对于有多方参与，且参与方在有限理性条件时的博弈过程缺乏相关分析和研究[7，8]。

工程建设过程中的安全监管属于社会性管制的范畴，其目的是希望相关安全监管部门对工程各参建方的具体行为是否符合相关法律、法规和工程建设标准的要求进行有效的控制，以期达到保障工程顺利进行，降低工程安全风险，较少事故数量和死伤人员数量的目的。安全监管的实际效果取决于监管方和被监管方的策略选择，各方的策略选择实际并非处于静止状态，而是随着时间的变化根据可观察了解到的各种信息在不断调整变化，呈现出复杂博弈的特性[9]。当存在有多个参建单位时，参建单位之间在面对监管时存在不同的利益诉求，因此，为了更好的反映实际情况，有必要对非合作关系下的多参与方安全监管问题加以分析研究。

为了更好地分析具有非合作关系的参建单位之间在安全监管部门与其之间长期的监督博弈动态过程，本文利用计算机仿真与理论证明相结合的方式，主要对监管部门与非合作关系条件下两参建单位之间的监督博弈演化过程进行建模与动态性分析，分析不同惩罚策略对博弈均衡和博弈过程的影响。

1 模型基本假定与描述

假定本文考虑的参建单位是基于追求利润最大化原则而进行自身策略选择的“经济人”。假定安全监管部门的监管能力足够强，且执法过程中不存在权利寻租，不存在违规操作的参建单位通过各种手段逃避处罚的情况，一旦检查必然能够查出其违章行为及违规操作程度。

假定安全监管部门有两个选择：检查和不检查，监管部门的策略是以α(0≥α≥1)的概率对建设项目进行抽样检查，日常检查平均成本为a(a>0)。参建单位同样有两个行动选择：按章办事和违规操作，考虑存在相互竞争的参建单位1与参建单位2，参建单位1的策略是以βi(0≤βi≤1,i=1,2)的概率选择按章办事，参建单位的正常生产收益为gi(i=1,2)，采用违章操作策略时获取额外的收益为hi(i=1,2)，造成的社会总体利益期望损失为bi，bi>0(i=1,2)。假设安全监管部门根据违章操作程度的情况对参建单位进行罚款，违章操作程度的情况可通过参建单位违规操作获取的额外收益hi(i=1,2)来反映。

当两个参建单位同时违规操作时，则项目一旦被检查到，则罚款为：

c=k(h1+h2)=c1+c2

(1)

当只有参建单位i违规操作，一旦被查处，则参建单位违规罚款为:

ci=khi(ci>0,k>1,i=1,2)

(2)

此时可以得到非合作关系的参建单位之间的博弈矩阵，如表1所示。

表1 参建单位间的博弈矩阵

假设参建单位收益(gi+hi-αci)>gi>(gi+hi-αc)，则该博弈为一个典型的斗鸡博弈，有两个Nash均衡：(按章办事，违规操作)，(违规操作，按章办事)，即参建单位有某一方违规时，另一方的最优策略是按章办事，反之亦然。

根据表1以及(1)式与(2)式，可以得到参建单位i的按章办事期望获益Uβi和预违规操作期望获益U1-βi分别为：

Uβi=gi

(3)

U1-βi=β-i·(gi+hi-αci)+

(1-β-i)·(gi+hi-αc)

(4)

则参建单位i的期望平均获益Ui为：

Ui=βiUβi+(1-βi)U1-βi

考虑安全监管部门随机与两个采用不同按章办事概率的参建单位中的任意一个进行博弈，获益矩阵如表2所示。

表2 安全监管部门收益矩阵

由表2可以得到监管部门进行抽样检查的期望获益Uα和不进行检查的期望获益U1-α分别为：

Uα=β1β2(-a)+β1(1-β2)(-a+c2-b2)+(1-β1)β2(-a+c1-b1)+(1-β1)(1-β2)(-a+c1-b1+c2-b2)

(5)

U1-α=β1(1-β2)(-b2)+(1-β1)β2(-b1)+(1-β1)(1-β2)(-b1-b2)

(6)

则监管部门的期望平均获益U为：

U=αUα+(1-α)U1-α

2 多方安全监管演化博弈

(7)

其中，U1-βi为参建单位i采用违规操作策略的期望获益，Uβi为参建单位i采用按章办事策略的期望获益，Ui为企业i的平均期望获益；Uα为安全监管部门抽样检查的期望获益，U1-α为安全监管部门不检查的期望获益，U为安全监管部门的平均期望获益。

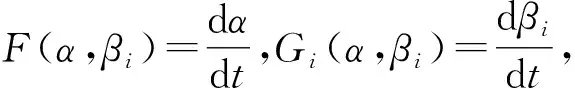
(8)

当惩罚策略为静态支付条件时，则对应策略支付值为常数。博弈参与者类型为有限理性时，往往会随机选择各自的初始策略。此时，当各方选择的初始策略不等于模型中的博弈均衡策略时，博弈过程将呈现出一个长期的波动状态，如果博弈均衡为一个演化稳定策略均衡(ESS)时，经过多次博弈后各方策略选择将收敛于均衡态；而当博弈均衡为非演化稳定策略时，博弈过程将处于震荡状态从而使分析更加困难。此时如果存在不完全信息的情况的话，则进程更为复杂。

当惩罚策略为动态支付条件时，即惩罚策略的收益支付与参建单位企业的违章操作概率相关，此时各博弈方达到博弈均衡的时间可以得到有效缩短，同时可以对博弈过程的波动性进行有效抑制。

在实际生活中，工程建设项目往往存在多个参建单位，而且单位之间并非完全独立，相互间存在各种各样的关系。受此影响，随着博弈参与者的增多，变量之间相互关系增多，完全求出(8)式的所有均衡点并对其进行稳定性分析十分困难，对各种策略函数条件下的演化稳定性理论分析难度也随之加大。模型分析的主要作用是抓住问题本质，分析各因素所带来的影响，从而最终找寻解决问题之道。因此，当模型分析无法完全利用理论分析达到最初的目的时，可以利用仿真手段，模拟不同政策策略的实施效果并进行科学的预测分析。

3 基于SD的演化博弈仿真

系统动力学(System Dynamic)是一种研究复杂系统中信息反馈行为有效的计算机仿真方法，在前面分析的基础上，本节将建立一个多人不对称演化博弈系统动力学(SD)仿真模型来研究安全监管博弈中各参与方之间的长期博弈关系以及其动态的行为趋势，从而研究各种影响因素和制定合理的监管提供一个有效的实验平台[13]。

3.1 仿真模型描述

用Vensim PLE 5.10e建立安全监管问题的演化博弈模型，模型的结构框架如图1所示。

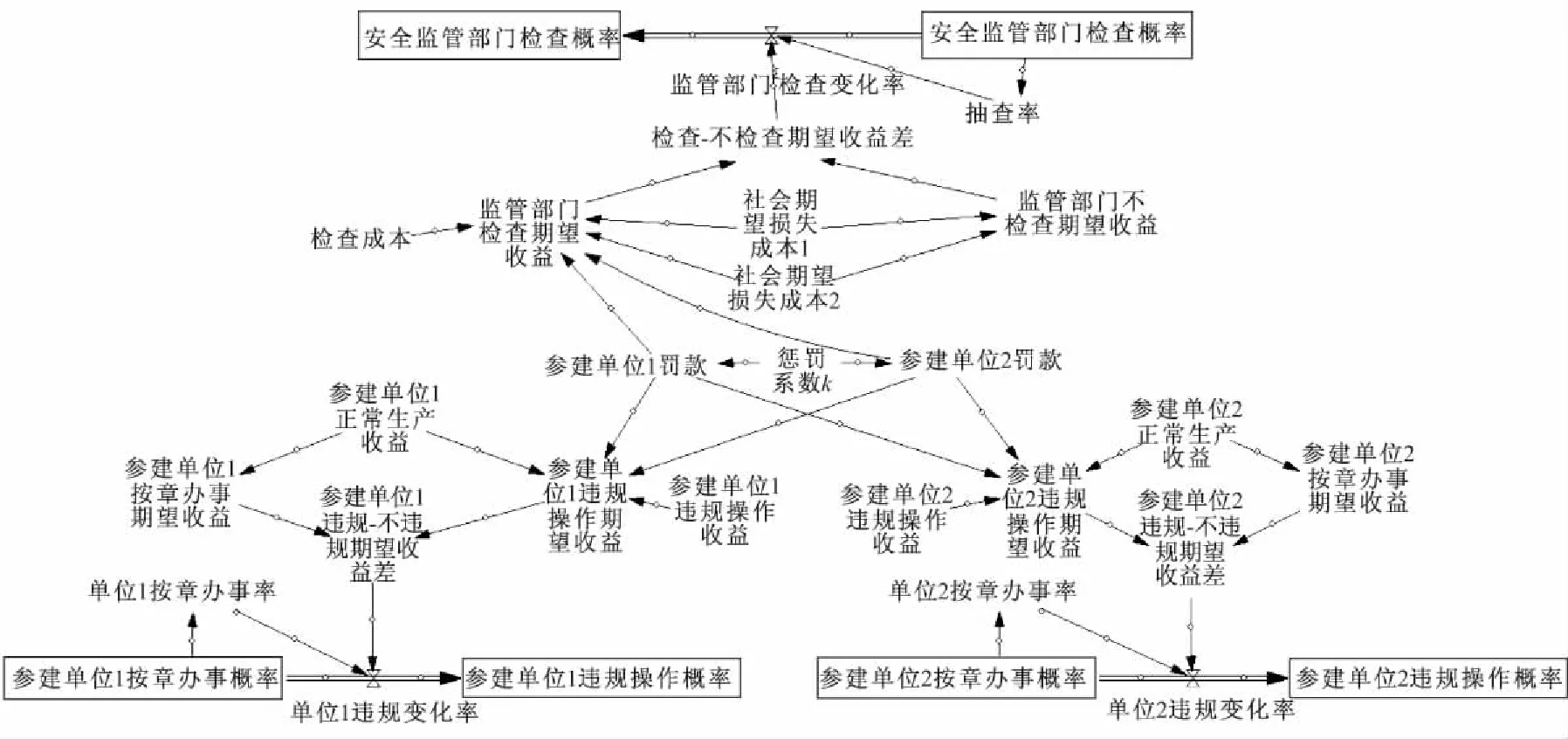
图1 安全监管多人演化博弈的SD模型

安全监管多人演化博弈的SD模型主要由6个流位、3个流率、18个中间变量和8个外部变量构成。参建单位1和参建单位2中采取按章办事策略的概率和采取违规操作策略的概率以及安全监管部门采取抽样检查的概率和采取不抽样检查的概率分别用6个流位变量来表示；参建单位1和参建单位2违规变化率以及安全监管部门采取抽样检查的概率变化率分别用3个流率变量来表示。外部变量分别对应表1和表2博弈支付矩阵中的8个变量取值。SD模型中流率公式及其涉及到的中间变量主要是根据前面分析得到变量之间的关系和演化博弈模型中的复制动态方程(8)式制定。

3.2 策略仿真分析

模型采用的软件为VensimPLE 5.10e，假设INITL4L TIME = 0, FINAL TIME=10000 , TIME STEP =1，假设监管检查成本a=1，参建单位1正常生产收益g1=10，违规操作收益h1=4，违规时造成的社会损失成本b1=5；参建单位2正常生产收益g2=5，违规操作收益h2=2，违规时造成的社会损失成本b2=2.5；惩罚系数k=2，初始值α=β1=β2=0.5。

3.2.1静态惩罚策略下系数k的影响

在静态支付条件下，随着系数k值的提高，参建单位在博弈均衡点时的违规操作概率βi也会随之下降。当考虑对象为两个参建单位时，惩罚系数k对参建单位策略选择的影响效果如图2、图3所示：

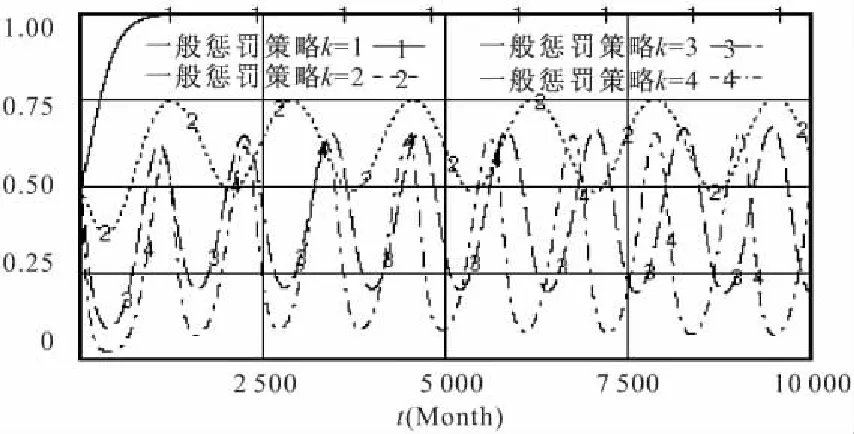
图2 不同惩罚系数对参建单位1的影响

图3 不同惩罚系数对安全监管部门的影响

图2中，曲线1～4分别表示在惩罚系数k=1，k= 2，k= 3和k=4不同惩罚额度的静态惩罚函数中，参建单位1违规操作概率1-β1的博弈演化过程。图3中的曲线1～4表示安全监管部门对应的抽查概率α的博弈演化过程。

由图2和图3所示的仿真结果可以发现，随着惩罚系数k的提高，参建单位平均违规操作概率和安全监管部门的平均抽查概率逐渐下降，同时博弈演化过程的波动的振幅和频率也随着惩罚额度的提高逐渐加大。在实际生活中，这一现象是普遍存在的，具体的表现为：当某地工程建设过程中有重大安全事故发生时，安全监管部门往往会立刻在第一时间采取更为严厉的管制政策，例如展开安全生产大检查等活动，参建单位获知这一信息时，随即减少自身的违规建设行为，从而安全形势将获得一个较好的控制效果。然而随着工程建设环境的好转，安全监管部门的控制措施将逐渐降低标准、放松对参建单位违规行为的监督力度，因为严格的管制政策将客观上加大安全监管的成本，此时，市场中的参建单位则会逐渐加大违规概率，从而又引起了建设安全问题的加重，最终形成实际安全形势反复波动，震荡发展的态势。

鉴于博弈过程中出现的波动性造成的安全控制情况反复情况，对于安全监管部门策略实施将带来一定的影响，使得其策略选择更加困难。并且，一味的执行严厉的惩罚策略，并不一定就能够达到控制违法违规的现象。Becker (1974)提出了通过严厉惩罚抑制犯罪的理论受到过不少研究者的质疑，并在不同领域中通过实证研究说明单纯的严厉惩罚策略往往不能够收到良好的实施效果，同时大部分被监管方也是能够遵守相关政策规定的，而在这样的情况下监管成本的提高是不经济的[14]。因此，一个良好的惩罚策略机制应该不是单纯的靠提高罚款的额度来降低违法行为的发生概率，而是应该在一个合理的水平上既能抑制违规违法行为，同时也能够避免造成监管博弈过程的波动性。

3.2.2静态惩罚策略与动态惩罚策略

博弈过程存在的反复波动现象，会给决策者带来决策选择上的困难，无助于问题的解决。相比于静态惩罚策略中惩罚系数为固定值的确定方式，根据被监管方的策略选择情况而动态的确定惩罚策略能够更加有效的抑制监管博弈演化过程中的波动现象。当考虑两个参建单位时，构建如下动态惩罚策略：

考虑对参建单位1与参建单位2同时采用动态惩罚函数(1-βi)khi，即在SD模型中添加以下变量关系式:

参建单位1罚款=参建单位1违规操作收益×惩罚系数k×参建单位1违规操作概率

参建单位2罚款=参建单位2违规操作收益×惩罚系数k×参建单位2违规操作概率

此时，可利用SD博弈模型对动态惩罚策略的效果进行仿真分析。

假设惩罚系数k=2，得到如图4所示仿真结果，曲线1和曲线2分别表示采取动态惩罚策略和静态惩罚策略时，参建单位1策略选择的演化过程。图5给出的是对应的监管部门策略选择的演化过程。

从仿真结果可以看出，动态惩罚策略与一般惩罚策略相比，能够有效地抑制博弈过程的波动性。但是，在相同的惩罚系数下，一般惩罚策略对参建单位违规行为的抑制效果要比动态惩罚策略好。因此，考虑存在多个参建单位时，采用动态惩罚策略在有效抑制博弈过程波动性的同时也提高了参建单位违规行为的博弈均衡值。

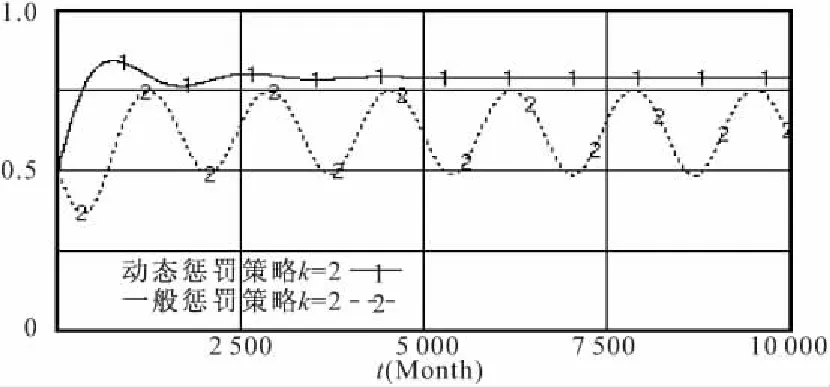
图4 不同惩罚策略对参建单位1的影响

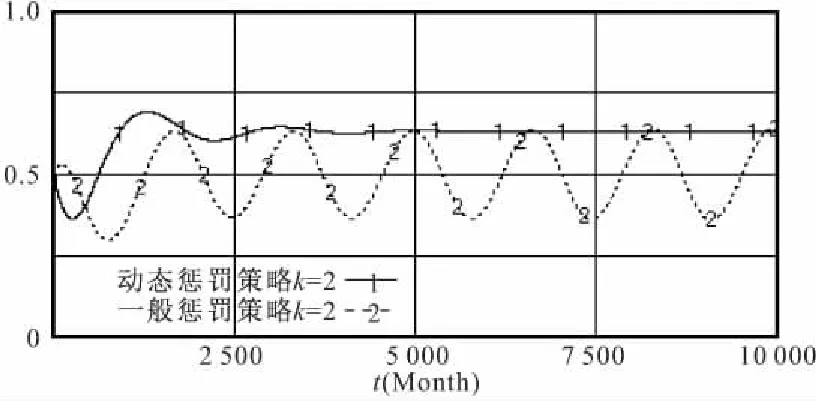
图5 不同惩罚策略对安全监管部门的影响

3.2.3博弈过程的稳定性分析

为了检验在博弈各参建方随机选择确定初始策略的情况下，采用静态惩罚策略和动态惩罚策略对博弈过程的稳定性的影响，对模型博弈各方初始策略在不同取值条件下进行仿真。

图6不同条件下初始值对参建单位1的影响

图7 不同条件下初始值对参建单位2的影响

图8 不同条件下初始值对安全监管部门的影响

图6、图7和图8中，曲线1与曲线2分别表示采用一般惩罚策略(k=3)时，博弈初始值分别为(α,β1,β2)=(0.1,0.1,0.1)和(α,β1,β2)=(0.5,0.5,0.5)的仿真结果;曲线3与曲线4则分别表示采用动态惩罚策略(k=2)时，博弈初始值分别为(α,β1,β2)=(0.1,0.1,0.1)和(α,β1,β2)=(0.5,0.5,0.5)的仿真结果；曲线5与曲线6则分别表示采用动态惩罚策略(k=2)时，博弈初始值分别为(α,β1,β2)=(0.1,0.1,0.1)和(α,β1,β2)=(0.5,0.5,0.5)的仿真结果。

通过仿真可以发现，当采用动态惩罚策略条件时，随着博弈方初始策略的改变，多次博弈后各方策略选择均收敛至稳定状态，由此可以看出，动态惩罚策略条件下演化博弈存在有演化稳定均衡(ESS)，此时博弈方的初始状态对博弈过程的动态性和均衡点并未造成太大的影响。而当采用静态惩罚策略条件时，随着博弈方初始策略的改变，多次博弈后各方策略选择始终处于波动状态，而且其波动的频率和幅度随着初始状态的变化而变化，无法收敛至稳定状态，以此可以推断静态惩罚策略条件下演化博弈不存在演化稳定均衡(ESS)，博弈结果难以预测。

由此可以看出，静态惩罚策略对于短期内降低安全风险，改善工程建设控制水平具有明显的效果，而采用动态惩罚策略则能有效地降低安全监管博弈过程中波动性，减少由于不确定性因素所造成的安全风险。安全监管部门进行策略选择和政策制定时，可以根据不同时期的主要工作目标，将静态惩罚策略与动态惩罚策略进行有机的结合，稳定地控制工程建设安全水平，减少安全事故的发生，营造更加良好的安全环境。

4 结 论

工程建设安全监管问题是一项系统工程，当存在有多个参建单位时情况更为复杂。本文考虑了存在非合作关系情况时，安全监管部门与两个参建单位之间的监督博弈演化模型，主要的工作和成果如下:

(1)考虑了各博弈参与方支付函数受各种因素影响，建立了一个多方演化博弈模型描述安全监管博弈关系，对在有限理性条件下对各方策略选择变化过程建立了求解方程，为研究多方安全监管博弈问题构建了理论框架；

(2)根据博弈模型建立了基于系统动力学的计算机仿真模型并进行了不同惩罚策略的仿真分析，通过仿真可以发现：

(a) 当监管方采用静态惩罚策略时，博弈过程不存在演化稳定策略(ESS)，但对应的收益(支付)值c将影响各方的策略选择，其中惩罚系数k的合理确定是主要问题。当k值太小的时候，由于参建方违规收益高于可能的惩罚支付，因此监管无法起到降低安全风险水平的作用，而一味提高k值时，博弈过程的波动性加剧，造成实际问题难以控制。

(b) 当监管方采用动态惩罚策略时，博弈过程存在演化稳定策略(ESS)，说明该策略可以较好的抑制博弈过程的波动状态，使安全问题可以达到预期的控制目标。然而，相同惩罚系数k值的条件下，动态惩罚策略对降低参建单位违规操作概率的力度逊于静态惩罚策略，客观上是由于此时对应收益(支付)c较小。

立足于各方博弈关系的研究对更好的实施安全监管有着积极的意义，但是博弈分析方法偏重于理论化和静态化，对于实际博弈过程的动态特性无法给予直观和准确的描述。因此，利用系统动力学原理辅以计算机仿真的途径，为研究复杂博弈问题提供了一条更为有效的解决之道。

[1] 中华人民共和国住房与城乡建设部. 建筑业发展“十二五”规划[R].北京:中华人民共和国住房与城乡建设部， 2011.

[2] 肖兴志，孙 艳. 中国建筑安全规制的博弈分析[J].产业经济评论，2009，8(2): 43-56.

[3] 袁海林，金维兴，刘树枫，等. 建筑企业安全控制的博弈分析及政策建议[J].建筑经济，2006，(11): 67-69.

[4] 曹冬平，王广斌. 中国建筑生产安全监管的博弈分析与政策建议[J].建筑经济，2007，(11): 52-55.

[5] 张玉娟，张飞涟，赖纯莹. 建筑市场安全监管的博弈分析[J].设计管理，2007，(1): 24-27.

[6] 黄海斌，王 平，蔡 睿. 建筑工程安全检查中的博弈分析[J].山西建筑，2008，34(27): 228-229.

[7] 谢识予. 有限理性条件下的进化博弈理论[J].上海财经大学学报，2001，3(5): 3-9.

[8] 张良桥，冯从文. 理性与有限理性:论经典博弈理论与进化博弈理论之关系[J].世界经济， 2001，(8): 74-78.

[9] 张维迎. 博弈论与信息经济学[M].上海:上海人民出版社，2004.

[10] Weibull J W. Evolutionary Game Theory[M]. The MIT Press，1997.

[11] Friedman D. On economic applications of evolutionary game theory[J]. Journal of Evolutionary Economics，1998，8(1): 15-43.

[12] Friedman D. Evolutionary games in economics[J]. Econometrica，1991，59(3): 637-666.

[13] Forrester J W. Industrial dynamics:a major breakthrough for decision makers[J]. Journal of the Operational Research Society，1997，48(10): 1037-1041.

[14] Becker G S. Crime and Punishment: An Economic Approach[R].Cambridge:UMI，1974.