轻质填充墙框架自振周期折减系数的取值研究

闫帅平, 夏文娟, 朱文静, 夏蕊芳

(1.济源职业技术学院， 河南 济源 454650； 2.中冶赛迪工程技术股份有限公司， 重庆 401122；3.中冶南方工程技术有限公司， 湖北 武汉 430074； 4.孝感学院， 湖北 孝感 432000)

钢筋混凝土框架结构是我国应用最广泛的结构体系，其填充墙一般为轻质砌块、空心砖和实心粘土砖等。试验研究和震害表明，地震作用下，填充墙与框架共同工作，一方面墙体受到框架的约束，另一方面框架受到填充墙的支撑。填充墙的支撑作用，使框架刚度大为增加，因此，计算框架自振周期时应考虑填充墙的作用，将计算所得框架的基本周期采用折减系数予以降低。周期折减系数的取值与诸多因素有关，如填充墙在结构平面、竖向的布置情况，填充墙的材质、数量，填充墙与框架的连接方式，填充墙上开洞情况等等，不能一概论之。但对比《高层建筑混凝土结构技术规程》(简称“高规”)2002版[1]与2010版[2]并未体现其差别。本文主要研究具有轻质填充墙的钢筋混凝土框架结构自振周期折减系数的取值问题。

1 模型验证

地震作用下，填充墙框架到达弹性极限位移时，填充墙内虽己出现大量斜裂缝，但裂缝一般不会贯通，墙体也没有达到其抗压强度，此时框架部分处于弹性极限状态。按此状态计算结构的自振周期，既考虑了填充墙的刚度作用，又不至于因刚度取值过大而使地震作用加大。取框架处于弹性阶段，考虑填充墙的作用，对结构进行模态分析。

按文献[3]所建模型，参考文献[4～7]，运用ANSYS软件对框架结构进行模态分析，通过对比填充墙为砖砌体的框架与空框架的自振周期验证本文模型的正确性。

模型中，钢筋混凝土框架的梁、柱、填充墙均用Solid65单元模拟，划分单元时保证所有的截面划分3层，可在层间根据实际布筋情况布置拉结钢筋单元，同时保证Solid65单元为六面体，三个方向尺寸比控制在10以内。拉结钢筋用Link10单元模拟，只承受拉力。模型保证了填充墙与框架只在框架平面内的水平方向相互约束。

算例为两等跨砖砌体填充墙多层钢筋混凝土框架，柱、梁混凝土柱强度等级分别为C30和C25；墙内拉结钢筋为HRB235级，沿柱高每500 mm设置两根直径为6 mm的拉结钢筋，钢筋伸进填充墙内1.5 m。具体为：①两等跨2～10层框架，跨度为9 m；②两等跨2～10层框架，跨度为6 m。算例基本信息见表1、表2，详细信息见表3。

表4给出了按ANSYS有限元模型，采用模态分析方法计算出的砖砌体填充墙框架自振周期、空框架自振周期以及与“高规”2002版[1]规定值之比。

表1 填充墙材料计算参数

表2 框架截面尺寸及配筋

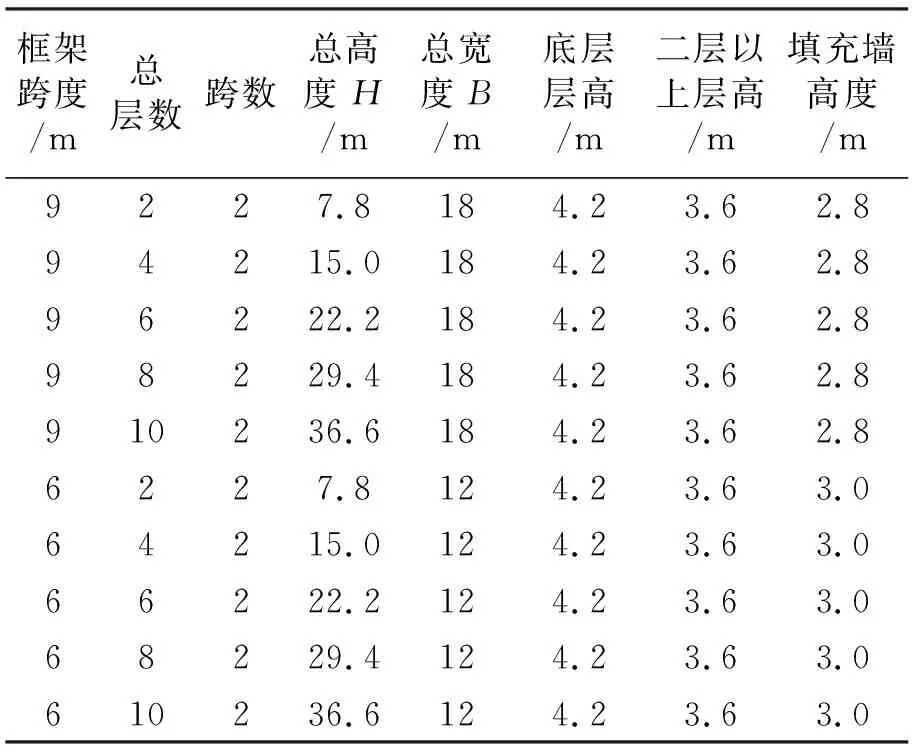
表3 空框架、砖填充墙框架、空心砌块填充墙框架信息

注：(1)空框架、砖填充墙框架、空心砌块填充墙框架均有表3所示10个算例;(2)填充墙高度一栏仅用于砖、空心砌块填充墙框架。

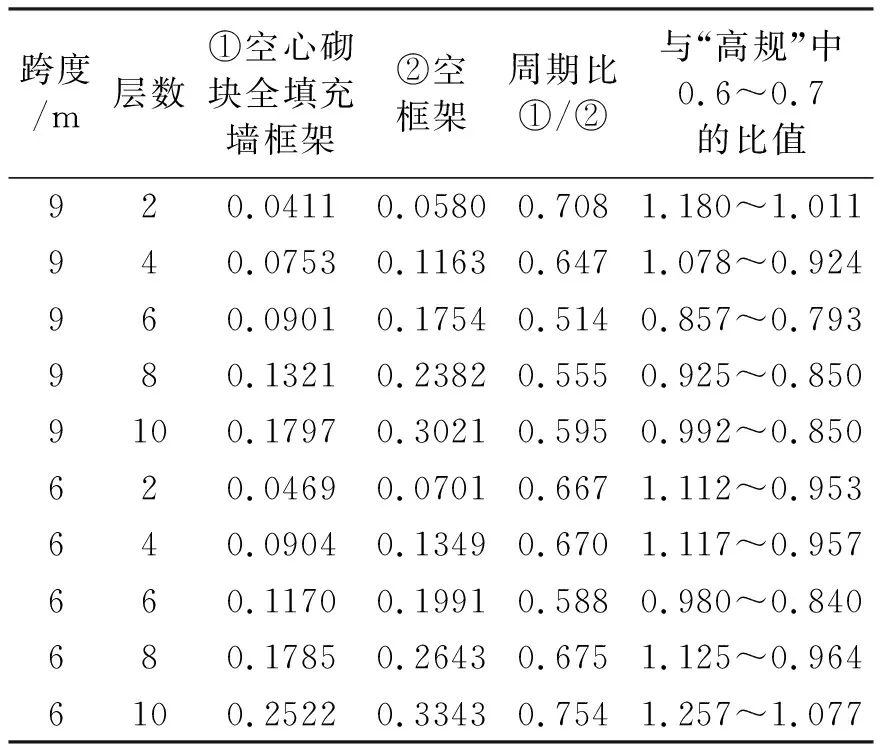
表4 砖填充框架与空框架自振周期比较

由表4可见，当框架填充墙为砖砌体时，9 m跨填充墙框架自振周期与空框架自振周期的比值为0.514～0.708，平均值为0.604，6 m跨其比值为0.588～0.754，平均值为0.671，两者总平均值为0.637，与“高规”2002版[1]建议取值0.6～0.7相当。从而验证了本文模型的正确性。

2 空心砌块填充墙框架自振周期折减系数

填充墙刚度和密度的不同，对结构自振周期的影响不尽相同。表5给出了按模态分析方法计算出的空心砌块填充墙框架自振周期、空框架自振周期以及与“高规”2010版[2]规定值的比值。

由表5可见，当框架填充墙为空心砌块时，9 m跨填充墙框架自振周期与空框架自振周期的比值为0.538～0.718，平均值为0.629，6 m跨其比值为0.621～0.734，平均值为0.697，总平均值为0.663。

由于空心砌块填充墙自身刚度及质量小于砖砌体，表5空心砌块填充墙框架的自振周期折减系数平均值大于表4砖砌体填充墙框架自振周期折减系数对应值。

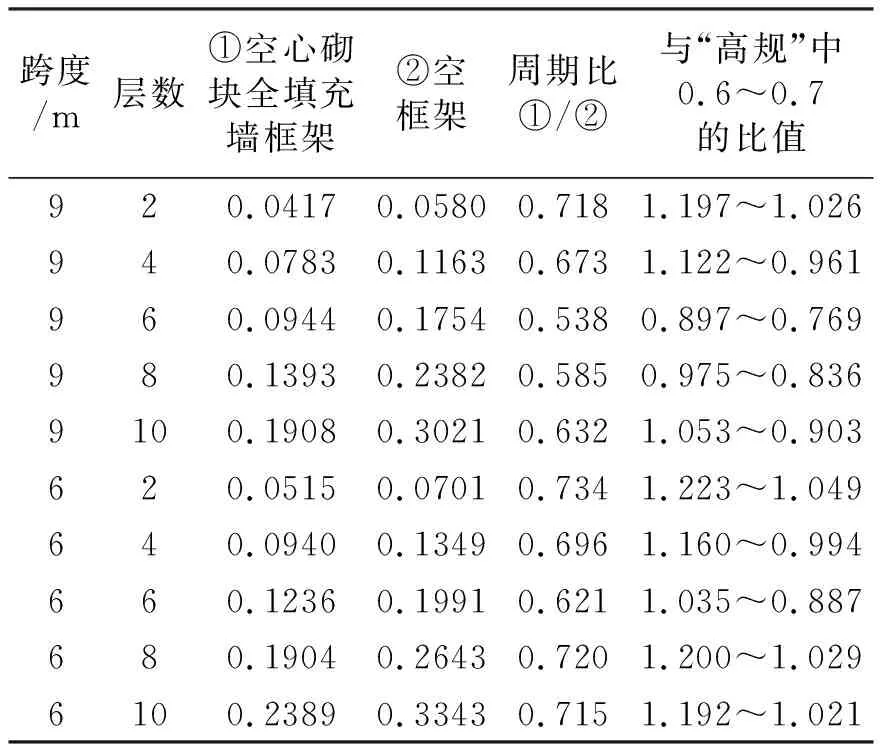
表5 空心砌块填充框架与空框架自振周期比较

图1给出了表4、表5求得的9 m等跨和6 m等跨全填充墙的框架结构自振周期折减系数与楼层的关系。

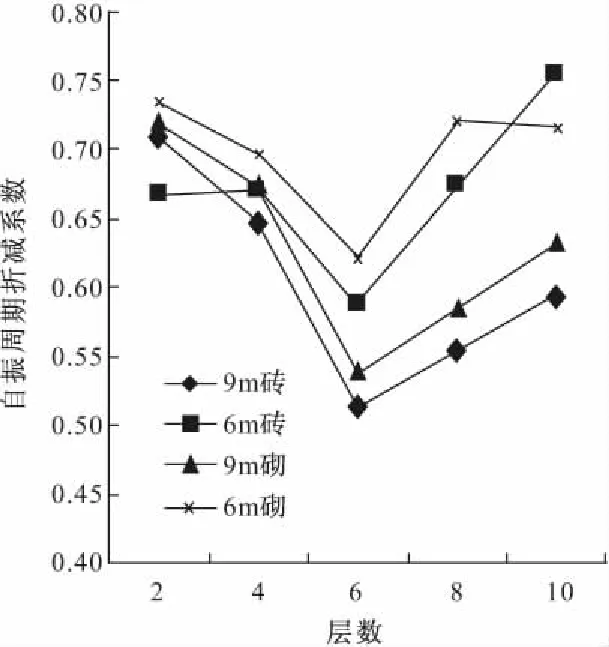
图1 不同跨度的框架自振周期折减系数对比

由图1可见，层数及高度相同时，跨度越小，全填充框架与空框架自振周期的比值越大。即随着跨度的减小，填充墙对框架结构自振周期的影响趋小，自振周期折减系数的取值变大。

当结构为6层时，结构自振周期折减系数为最小；小于6层时自振周期折减系数，随层数的增加而递减；大于6层时，自振周期折减系数随层数的增加而增加。对于低层建筑，自振周期折减系数宜取接近0.6，对于7～10层建筑，宜取接近0.7。

3 底层无填充墙框架与空框架、全填充墙框架自振周期的比较

底层无填充墙框架与空框架、全填充墙框架相比较为不利，研究底层无填充墙框架结构自振周期十分必要。表6给出了填充墙为空心砌块的全填充墙框架、底层无填充墙框架及空框架自振周期。由表6可知，当框架填充墙为空心砌块时，9 m跨底层无填充墙框架与空框架自振周期的比值为1.215～1.372，平均值为1.288，6 m跨其比值为1.137～1.327，平均值为1.215，总平均值为1.252。9 m跨底层无填充墙框架与全部填充的框架自振周期的比值为1.909～2.378，平均值为2.061，6 m跨其比值为1.591～1.973，平均值为1.748，总平均值为1.905。

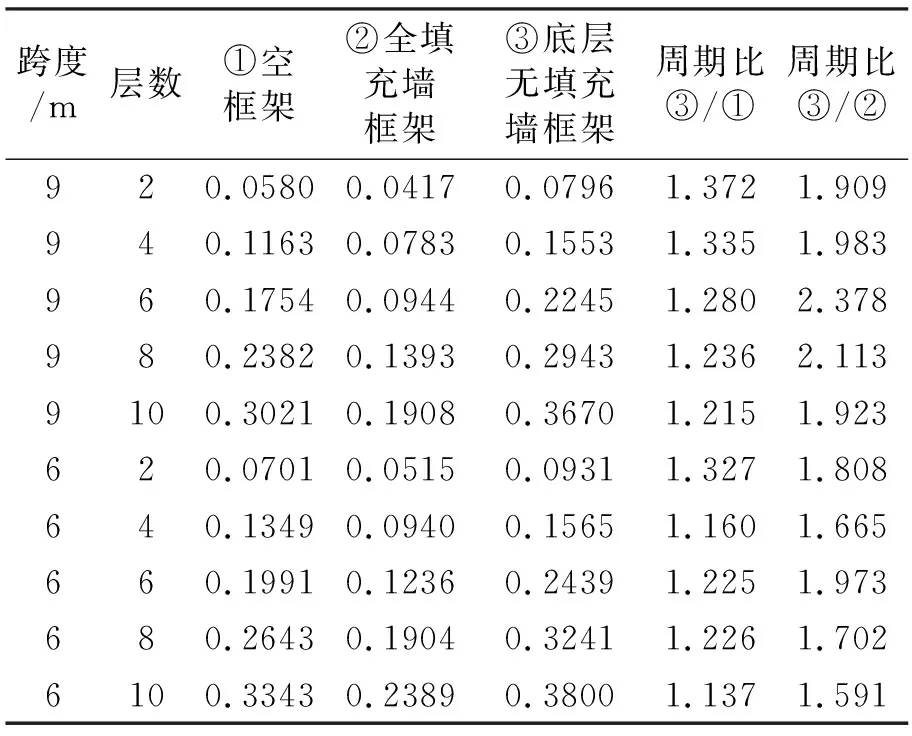
表6 空心砌块全填充墙框架、底层无填充墙框架、

表7给出了填充墙为砖砌体的全填充墙框架、底层无填充墙框架及空框架自振周期。由表7可见，当框架填充墙为砖砌体时，9 m跨底层无填充墙框架与空框架自振周期的比值为1.112～1.240，平均值为1.171，6 m跨其比值为1.115～1.245，平均值为1.153，总平均值为1.252。9 m跨底层无填充墙框架与全部填充的框架自振周期的比值为1.749～2.267，平均值为1.957，6m跨其比值为1.507～1.897，平均值为1.727，总平均值为1.832。

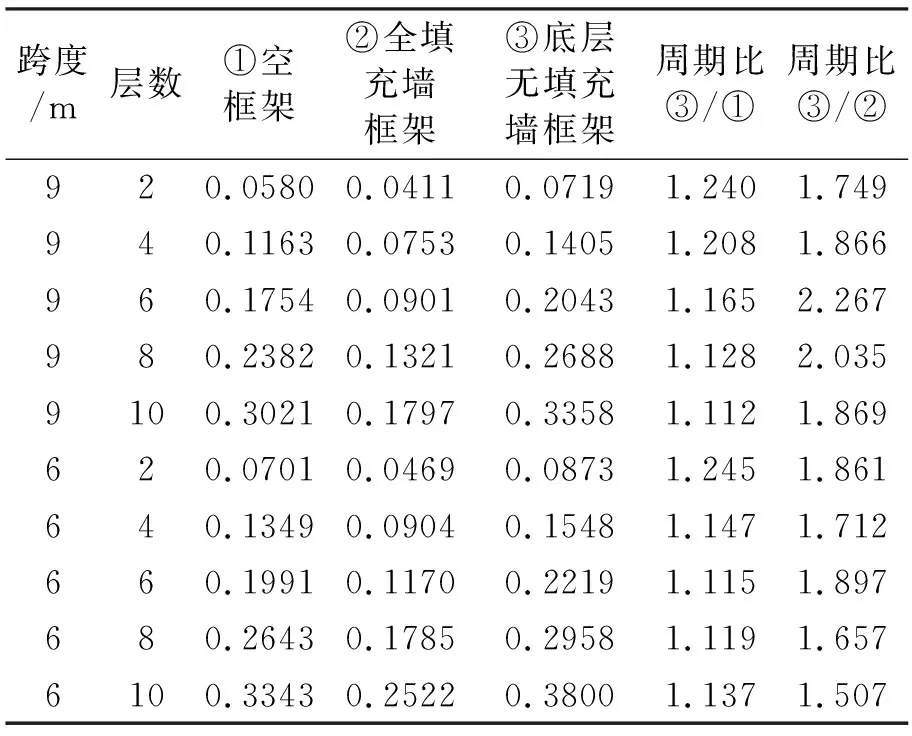
表7 砖砌体全填充墙框架、底层无填充墙框架、

由表6、表7可见，底层填充墙对框架结构刚度贡献大，若底层薄弱，随着跨度的增大，结构上部刚度突变程度增大，填充墙对框架结构自振周期的影响增大，导致底层无填充墙框架变形加大，周期变长。层数及层高相同时，跨度越大，自振周期增大的效果越明显。

由上述可见，计算底层无填充墙框架自振周期时，应考虑由底层无填充墙导致的自振周期增大。

4 填充墙位置及填充率对空心砌块框架自振周期的影响

现代建筑为了满足使用功能的要求，通常只在部分楼层或部位设置填充墙。已建填充墙的面积与框架填满填充墙时填充墙面积的比值，用填充率表示。

4.1 填充率为87.5%

当框架存在一个薄弱层，填充率为87.5%时，框架计算模型见图2，图2中 (a)～(h)分别表示在第1、2、3、4、5、6、7、8层没有设置填充墙。周期比较见表8。

图2 填充率为87.5%时，框架计算模型

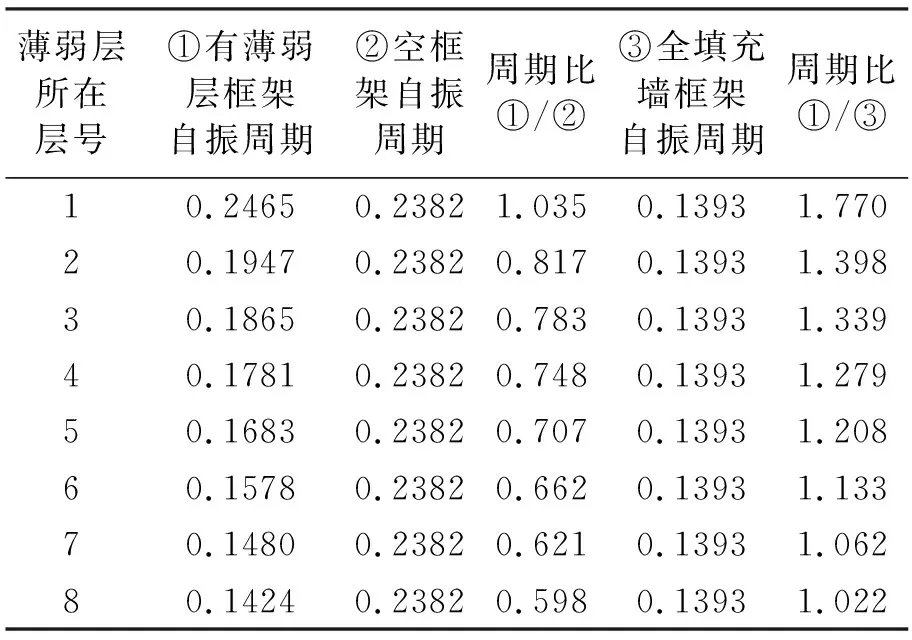
薄弱层所在层号①有薄弱层框架自振周期②空框架自振周期周期比①/②③全填充墙框架自振周期周期比①/③10.24650.23821.0350.13931.77020.19470.23820.8170.13931.39830.18650.23820.7830.13931.33940.17810.23820.7480.13931.27950.16830.23820.7070.13931.20860.15780.23820.6620.13931.13370.14800.23820.6210.13931.06280.14240.23820.5980.13931.022

由表8知，底层填充墙对框架自振周期影响最大；薄弱层的位置越靠上，对框架自振周期影响越大，自振周期折减系数越小，接近“高规”2010版[2]规定的下限值0.6，有薄弱层框架自振周期与无薄弱层框架自振周期的差别越小。

4.2 填充率为73%

框架底层无填充墙，上部存在一个薄弱层,填充率为73%时，框架计算模型见图3，图3中 (a)～(f)分别表示在第1层和3层、1层和4层、1层和5层、1层和6层、1层和7层、1层和8层没有设置填充墙。其自振周期计算结果及比较见表9。

图3 填充率为73%时，框架计算模型

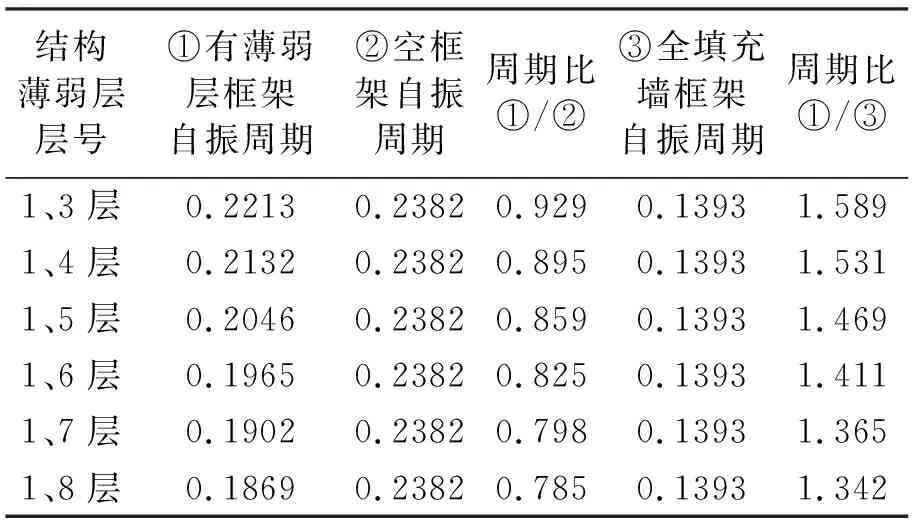
结构薄弱层层号①有薄弱层框架自振周期②空框架自振周期周期比①/②③全填充墙框架自振周期周期比①/③1、3层0.22130.23820.9290.13931.5891、4层0.21320.23820.8950.13931.5311、5层0.20460.23820.8590.13931.4691、6层0.19650.23820.8250.13931.4111、7层0.19020.23820.7980.13931.3651、8层0.18690.23820.7850.13931.342

由表9可见，薄弱层的位置越靠上，自振周期折减系数的取值越小，折减系数的取值集中在0.8～0.9之间。具有两个薄弱层的框架自振周期较全填充框架增加显著，但随着薄弱层的位置的靠上，其差别趋于减小。

4.3 填充率为50%

框架存在多个薄弱层，填充率为50%时，填充墙在不同位置对框架自振周期的影响计算模型见图4，图4中(a)表示在第5～8层没有设置填充墙，(b)表示填充墙隔层隔跨布置，(c)表示填充墙布置在左跨，(d)表示在第3、4、7、8层不设填充墙，(e)表示在第2、4、6、8层不设填充墙，(f)表示在第1、3、5、7层不设填充墙。框架自振周期的变化见表10。

由表10可见，填充墙沿楼层分布越密集、越靠近框架下部，自振周期折减系数的取值越小，当框架填充墙集中在结构下部时，周期折减系数的取值最小，与《高规》2010[2]给定的取值范围0.6～0.7接近。自振周期折减系数根据图4所示的布置递增。

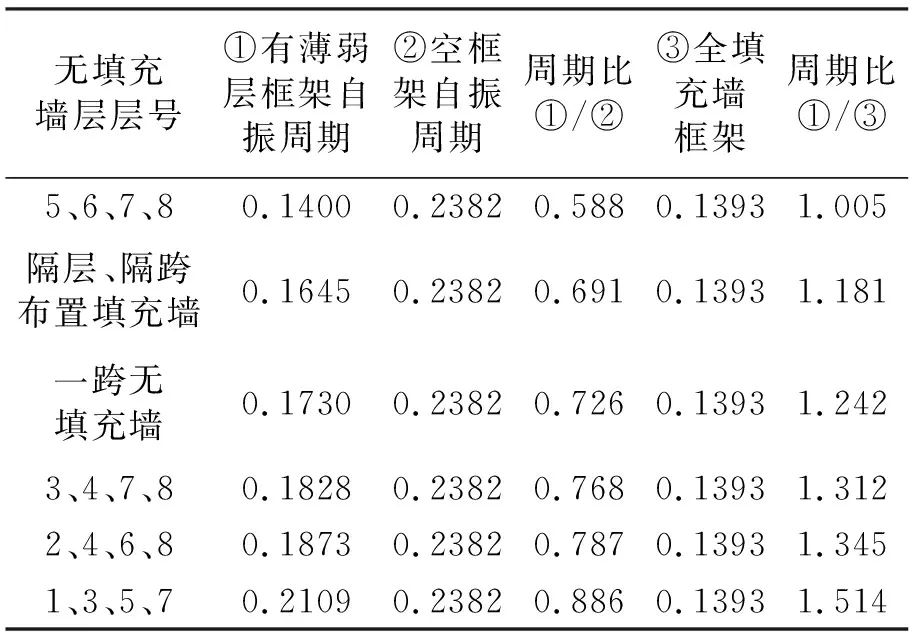
表10 填充率为50%，填充墙在不同位置时，

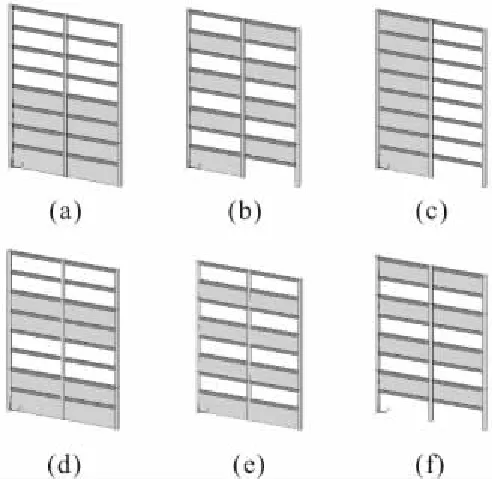
图4 填充率为50%时，框架计算模型

4.4 填充率为12.5%

填充墙位于不同层、填充率为12.5%时，其自振周期计算结果及比较见表11。由表11可见，填充墙在不同层时，对框架自振周期的影响不同，随着层数的增加，填充墙对框架的影响逐渐减小；当填充墙置于顶层时，填充墙对框架的影响又急剧增大。

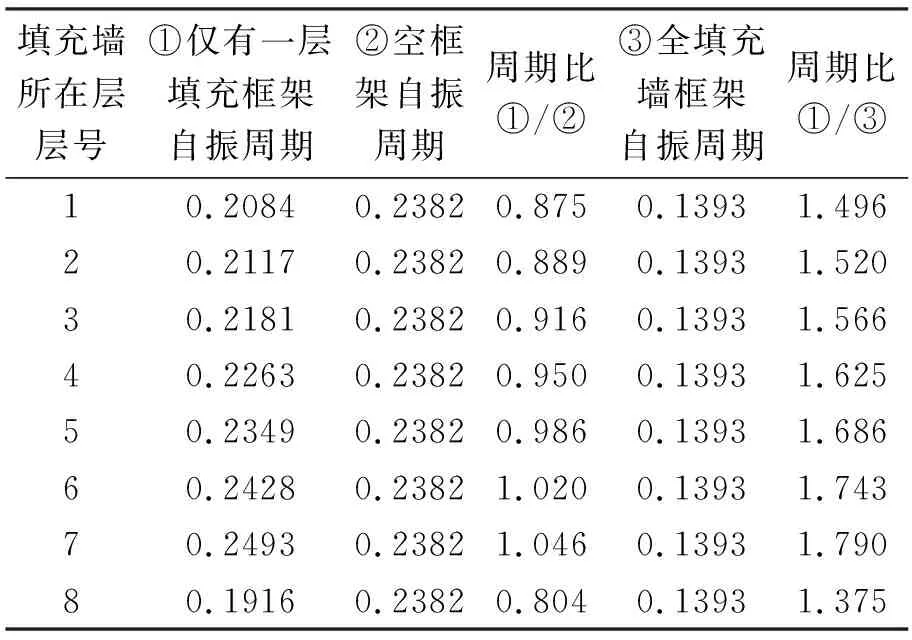
表11 填充率为12.5%时，填充墙框架

为便于工程应用，综合表8、表9、表11，将不同填充率的框架自振周期折减系数进行线性回归，见表12。由表12可见，填充率越高，框架结构自振周期折减系数的取值越小，框架自振周期折减系数随填充墙分布的高度呈线性变化。

表12 空心砌块填充墙框架自振周期折减系数回归公式

5 结 论

(1)空心砌块填充墙框架周期折减系数大于砖砌体填充墙框架周期折减系数，对于空心砌体填充墙框架结构，在“高规”2010版取值0.6～0.7的基础上，宜适当增大。

(2)计算底层无填充墙框架自振周期时，应考虑由底层无填充墙导致的框架自振周期增大。

(3)结构存在薄弱层时，自振周期折减系数取值与薄弱层所在位置和填充率有关，薄弱层的位置越靠上、填充率越高，自振周期折减系数取值越小，自振周期折减系数的取值可参考表12所示回归公式。

(4)当填充率为50%时，填充墙在不同位置时自振周期折减系数可参考表10取值。

[1] JGJ 3-2002，高层建筑混凝土结构技术规程[S].

[2] JGJ 3-2010，高层建筑混凝土结构技术规程[S].

[3] 闫帅平.填充墙对框架结构自振周期影响的研究 [D].武汉：华中科技大学，2008.

[4] 朱荣华，沈聚敏.砖填充墙钢筋混凝土框架拟动力地震反应试验及理论分析[J].建筑结构学报，1996，17(4)：27-34.

[5] 曾晓明，杨伟军，施楚贤.砌体受压本构关系模型的研究[J].四川建筑科学研究，2001，(3)：8-10.

[6] Buonopane S G, White R.N. Pseudodynamic testing of masonry infilled reinforced concrete frame[J].Journal of Structural Engineering,1999,125(6)：578-589.

[7] 邹 昀.多层多跨带砌体填充墙的钢筋混凝土框架强度分析[J].江南大学学报，2003，2(2)：186-189.

[8] 包世华，方鄂华.高层建筑结构设计[M].第二版.北京：清华大学出版社，1996.