广义k集元第二类Stirling数若干结论
黄荣辉
(1.华南师范大学数学科学学院,广东 广州510631;2.顺德碧江中学,广东 广州528311)
1 引 言
对于一般的或广义的第二类Stirling数的研究已有大量的文献,得出了一系列的结论[1-6].而本文将第二类Stirling数的部分条件改变,即改变其集合个数,因此而给出了新定义的广义多元集第二类Stirling数,并得出相关结论,其结论在现实生活中也有着一定的运用.先给出以下有关定义及相关引理.
定义1[1]从n个不同事物中每次取出m 个的组合数,记作C(n,m).
定义2 把含有n个元素的一个集合分成恰好有r个非空子集合的分拆数目就叫做第二类Stirling数,并记作S2(n,r),对于n=r=0,定义S2(0,0)=1及n<r时,S2(n,r)=0.
定义3 把分别含有n和m个元素的集合A和集合B共同分成恰好有r个非空子集合,且每个子集必须同时含有集合A和集合B的元素的分拆数目就叫做广义二集元第二类Stirling数,并记作S2({n,m},r),定义S2({0,0},0)=1及n<r或m <r时,S2({n,m},r)=0.这里规定集合A和集合B 没有公共元素.
定义4 设集合Ai(i=1,L,k)分别含有Ji(i=1,L,k)个元素,将集合A=UAi(i=1,L,k)分成恰好有r个非空子集合,且每个非空子集必须同时含有集合Ai(i=1,L,k)的元素的分拆数目就叫做广义k集元第二类Stirling数,并记作S2({J1,L,Jk},r),定义S2({0,L,0},0)=1,若存在i∈ {1,L,k},使得Ji<r时,则S2({J1,L,Jk},r)=0,同样规定集合Ai(i=1,L,k)两两不相交.
以下是对本文证明有关的引理.
引理1[1]当n≥1时,S2(n,2)=2n-1-1.

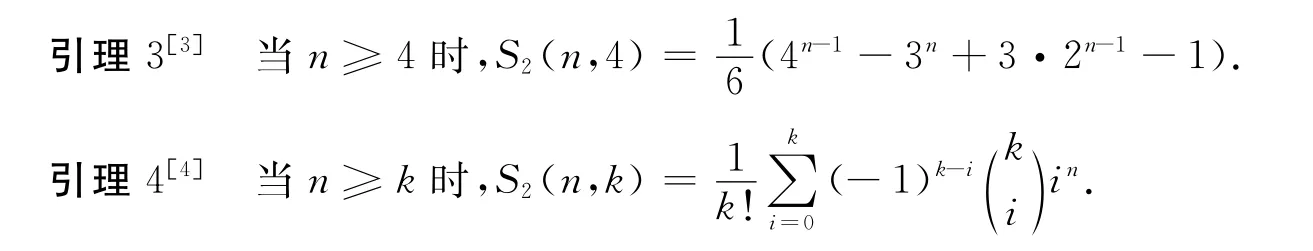
2 主要结论及证明
定理1 当n,m ≥1时,S2({n,m},2)=2n+m-1-2n-2m+2.
证明 不妨记集合Ai(i=1,2)的元素个数分别为n,m,则由广义二元集第二类Stirling数的定义可知,即将两个集合共同分拆成两个非空子集,并且要求每个子集至少含有任一集合的一个元素.这种规定实则意味着可以先将其中一个集合划分成两个非空集合A1i(i=1,2)后再将第二个集合按照规定进行分配,而第二个集合同样需要符合定义中的规定,因此也必须将其分成两个非空集合A2i(i=1,2),然后再将这两种分拆重新组合形成两个集合,有如下形式:

证毕.
定理2 当n,m≥2时,有

证明 记集合Ai(i=1,2)的元素个数分别为n,m,同定理1的证明,先将集合A1分划成3个非空集合A1i(i=1,2,3),再将集合A2分划成3个非空集合A2i(i=1,2,3),其重新组合成3个集合种类形如

故其组合种类共有3!类,从而
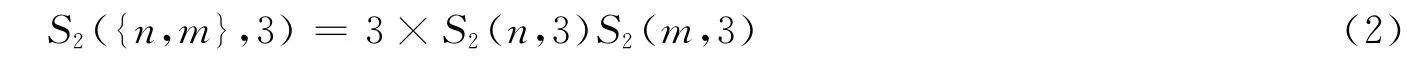
再由引理2的结论,合并整理 (2)式即可得此定理.
由以上两个定理的结论可知当,当分划非空子集个数越多时,其表达式越复杂,以下给出广义二元集第二类Stirling数与第二类Stirling数的关系式.
定理3 当n,m ≥k时,S2({n,m},k)=k!S2(n,k)S2(m,k).
证明 记集合Ai(i=1,2)的元素个数分别为n,m,同以上定理的证明,先将集合A1分成k个非空子集A1i(i=1,2,L,k),同理集合A2也分成k个非空子集A2i(i=1,2,L,k),同上述定理的证明思想,可得一般的广义二元集第二类Stirling数的结论如下:
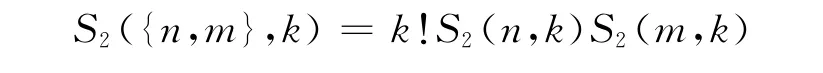
证毕.
以上是对于两个集合的情况,下面对于一般的情况进行讨论.
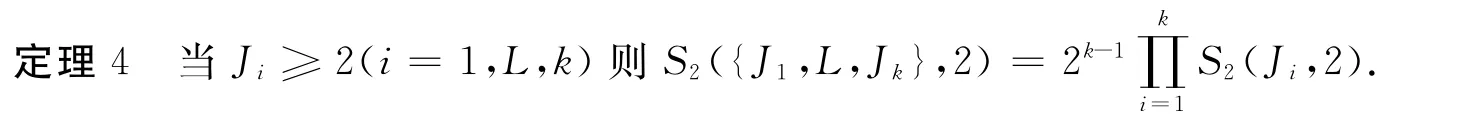
证明 设集合Ai(i=1,L,k)分别含有Ji(i=1,L,k)个元素,且集合Ai(i=1,L,k)互不相交.则根据定义可知,先将Ai(i=1,L,k)依次分成两个非空子集Aij(j=1,2),则共同分划成两个非空子集类型如下

同样的分析可得如下几个定理.

[1] 陈景润.组合数学简介 [M].天津:天津科学技术出版社,1988
[2] Du CY.An equation of stirling numbers of the second kind [J].Chin Quart J Math,2006,21:261-263
[3] Liang WX.An identity of stirling numbers of the second kind[J].Scientia Magna,2006,(02):40-43
[4] 李朝星.第二类Stirling数的等价表示式 [J].湖北师范学院学报:自然科学版,1990,09(02):111-120
[5] 黄荣辉,陈宝儿.广义第二类Stirling数的一些结论 [J].韩山师范学院学报,2011,(03):29-31
[6] 张福玲.第二类Stirling数的一个恒等式 [J].西南民族大学学报:自然科学版,2009,35(04):741-743

