一类奇异线性反应扩散方程组的解

郭高荣

（安阳工学院数理学院，河南 安阳455000）

1 引 言

文献 ［1］讨论了一类奇异半线性反应扩散方程初值问题整体解的存在性唯一性及解的增长性.文献［2－3］讨论了一类半线性奇异反应扩散方程组解的爆破性，但对这样一类特殊的奇异半线性发展方程组的解研究比较少见.这里需要说明的是用Fourier变换法很容易得到如下二元奇异线性反应扩散方程组的解，但是我们用另一种方法来解决它，同时用这种方法可以得到N元奇异线性反应扩散方程组解.

2 正 文

本文讨论如下二元奇异线性反应扩散方程组解的估计式.

其中u0（x），ν0（x）∈L∞（RN），u0（x）≥0，ν0（x）≥0，且u0（x），ν0（x）不恒为零.为书写方便，有时把u（t，x）记为u（t）或u，ν（t，x）类似.

问题 （1）（2）在带形区域ST＝ （ε，T）×RN中有广义解（u（t，x），ν（t，x）），其含义是函数对（u（t，x），ν（t，x））在ST满足 （1）（2）式，且对一切ε＜τ＜T，该函数对在带形区域Sτ中有界.以下简称这样的函数对为解.

引入有界线性算子半群 T（t）如下：任给φ（x）∈Lp（RN）（1≤p ≤ ∞），（T（t）φ（x）＝∫RNGt（xy）φ（y）dy，其中Gt（x）＝ （4πt）－N／2exp［－x2／（4t）］.

与问题 （1）（2）相应的积分方程为：

引理2 设u0（x），ν0（x）∈L∞（RN），u0（x）≥0，ν0（x）≥0，且u0（x），ν0（x）不恒为零，则问题（1）（2）的非负非平凡解 （u（t，x），ν（t，x））满足下式：

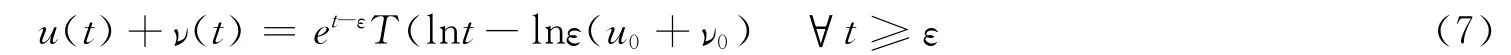
证明 由（3）式知u（t，x）≥T（ln t－lnε）（u0＋ν0）

将上式代入（4）式得ν（t，x）≥T（l n t－l nε）ν0＋（t－ε）T（l n t－l nε）u0

由Gr on wall不等式，得

由（10）（11）得（7）式.引理得证.

引理3 设u0（x），ν0（x）∈L∞（RN），u0（x）≥0，ν0（x）≥0，且u0（x），ν0（x）不恒为零，则问题（1）（2）的非负非平凡解 （u（t，x），ν（t，x））满足下式：

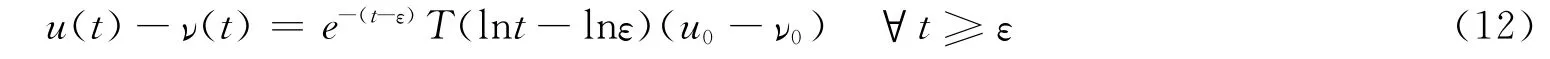
证明 由（9）得

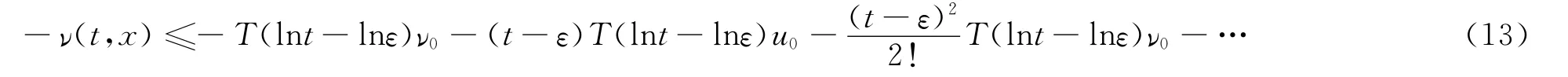
将（11）式中的et－ε展开成（t－ε）的幂级数，结合（13）得

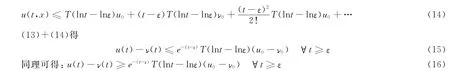
由（15）（16）得（12）式.引理得证.

由引理2与引理3整理可得下面的定理：

定理1 设u0（x），ν0（x）∈L∞（RN），u0（x）≥0，ν0（x）≥0，且u0（x），ν0（x）不恒为零，则问题（1）（2）的非负非平凡解的集合可由下列函数给出：

其中φi（x）∈L∞（RN），φi（x）≥0，且φi（x）不恒为零.

用上述方法可以得到问题（17）解的集合如下：

［1］彭大蘅，王志成，苏醒，等.一类奇异半线性反应扩散方程初值问题整体解的存在性唯一性及解的增长性［J］.数学学报，2001，22 A：（04）：483－490

［2］彭大蘅，韩茂安，王志成，具奇异系数反应扩散方程组Cauchy问题［J］.数学物理学报，2005，25 A（02）：220－229

［3］彭大衡，韩茂安，奇异半线性反应扩散方程组Cauchy问题［J］.数学年刊，2004，25 A（06）：23－29

［4］Escobedo M，Herrero MA.Boundedness and blow up for a semilinear Reaction－diffusion system［J］.J differ equat，1991，89，176－202