残余应力影响下的圆锥压入问题

孙 渊

（上海电机学院 机械学院，上海 200245）

残余应力影响下的圆锥压入问题

孙 渊

（上海电机学院 机械学院，上海 200245）

利用有限元分析了材料在压痕过程中各变量，并计算了硬度HRC值，与在硬度试验中所测HRC值吻合，证实了有限元分析的正确性；在此基础上，分析了试件具有残余应力时的压入响应问题，研究了残余应力对圆锥压入响应的影响，探讨了压痕法测试残余应力所存在的问题。研究结果表明：残余拉、压应力以不同程度影响压入响应，压应力使圆锥压头处出现隆起量，而拉应力使其出现下沉量，该表现用于直观法预测残余应力；拉应力使压痕处塑性区域增加，压应力使塑性区域减少，在压痕法测量残余应力时，由于塑性区域事先的未知性而影响应变测试位置的确定，从而影响测量残余应力的准确性。

残余应力；压入响应；塑性区域；测试位置不确定性

压入问题是指用一定几何形状的压头对固体材料表面实施准静压加载，考察材料的压入响应进而获得材料基本力学性能参数的问题。当材料表面具有不同的力学性能，特别是不同的残余应力时，会呈现出不同的压入响应。压入响应是描述刚性压球压向弹性半空间的材料，当材料发生塑性变形时，压痕处发生的弹塑性行为，即压痕深度、回弹量、隆起量、压痕塑性区域及压痕接触应力等。目前，利用硬度试验方法进行压入问题的研究在材料性能以及残余应力测试技术中的应用越来越得到有关研究人员的关注［1－7］，通过压痕硬度试验研究金属材料的变形机理，了解压入过程，描述压入响应与材料力学性能的关系、压入响应与材料残余应力的关系。

压痕技术可用于研究小尺寸器件的力学性能［6－7］，如薄膜和涂层材料，它们的材料性能一般不宜通过拉伸试验的办法测量得到；而在残余应力的测试技术研究中，大多数学者采用布氏压头和圆锥压头进行局部载荷压入问题的研究［8－14］，描述材料在残余应力场下的压入问题。

本文采用金刚石圆锥压头进行压入响应的有限元分析和实验研究，分析残余应力对压入响应的影响，描述它们之间的关系，特别是局部载荷下残余应力对弹塑性边界的影响，从而探讨利用压痕法测试残余应力过程中应变片位置确定所存在的问题。相对于布氏压头，圆锥压头能应用于洛氏硬度HRC50的试件，所用的载荷较小，而且试样表面粗糙度对压入响应的准确性影响也较小。

1 硬度试验和材料性能测定

洛氏硬度试验法可采用120°金刚石圆锥作为压头，在预负荷100N作用下，压头压入试样深度为h1，反映硬度值的压入深度从h1这一位置开始计算；分别加上500N或900N主负荷，即在总负荷为600N或1kN的作用下，将压头压入试样表面，压入试样深度为h2；卸除主负荷，由于试样的回弹能力而产生一定的回弹量，此时压入深度为h3。压入示意图如图1所示。卸除主载荷，在保留预负荷下测量压头压入试样表面的深度，通过一定的关系来反映洛氏硬度值的高低，如用C标尺则为HRC，其洛氏硬度计算公式为

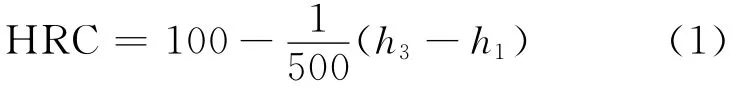
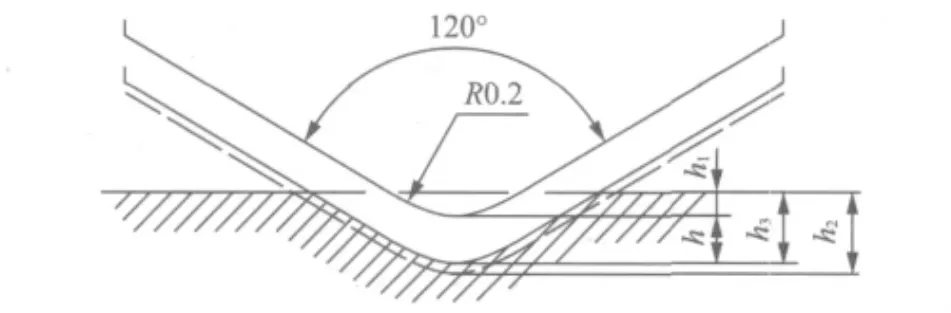
图1 洛氏硬度压入示意图Fig.1 Sketch of Rockwell hardness indentation

从实验过程原理和计算公式可见，洛氏硬度实验是在同样实验条件下，以压头压入试样的深度来反映材料的硬度。h＝h3－h1描述为在总负载作用下，卸除主负荷保留预负荷时，压头实际压入的残余深度，h越大，硬度愈低；h愈小，硬度愈高。

试件材料采用40Cr和45钢，经调质处理，提高了材料的硬度，其力学性能如表1所示。

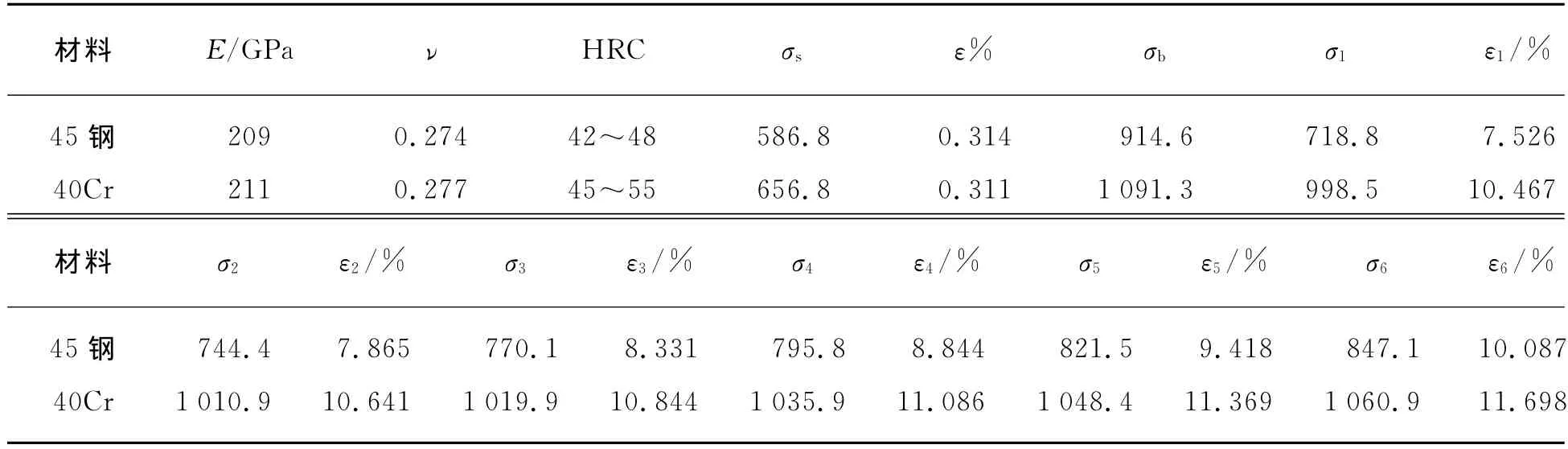
表1 40Cr和45钢材料力学性能实验数据Tab.1 Material property of 40Cr and 45steel

2 有限元分析

2.1 模型建立

根据洛氏硬度试验原理建立有限元计算模型。为提高网格质量和减少单元数量，将被测试样简化为2.5mm×2.5mm（满足国标中试样厚度不小于残余压痕深度的10倍的要求）的等边三角形面；参考GB／T 230.1—2009《金属材料 洛氏硬度试验》要求，圆锥压头锥角为120°，顶部曲率半径为0.2mm。如图2所示。根据对称性，选取试件和压球的1／4建立几何模型，被测试样单元采用高精度六节点三角形单元PLANE183（轴对称），压入过程为高度大变形且有塑性变形，采用三角形单元。计算表明：结果易收敛，计算时间短。为减少计算量，且在接触处得到良好的计算结果，故接触处网格划分较密，远处较疏。选定压球为刚性目标面，试件为接触面，输入试件的材料特性，包括：弹性模量E、泊松比ν、屈服应力σs、塑性区域的应力σ1～σ6及应变量ε1～ε6等（见表1），定义边界条件，加载求解。

图2 有限元模型Fig.2 Finite element model

2.2 压痕过程中的各变量

通过有限元分析，得到了不同载荷下的压痕参数，表2、3分别为在不同载荷P作用下得到的45钢与40Cr的各变量：加载时压入深度、隆起量，卸载后压痕深度、隆起量、回弹量、塑性区域表面半径及深度。通过式（1）计算得到硬度值，与实验所测数据进行比较，吻合程度较高，说明有限元分析过程中参数设置、技术运用方法合理，分析结果正确。

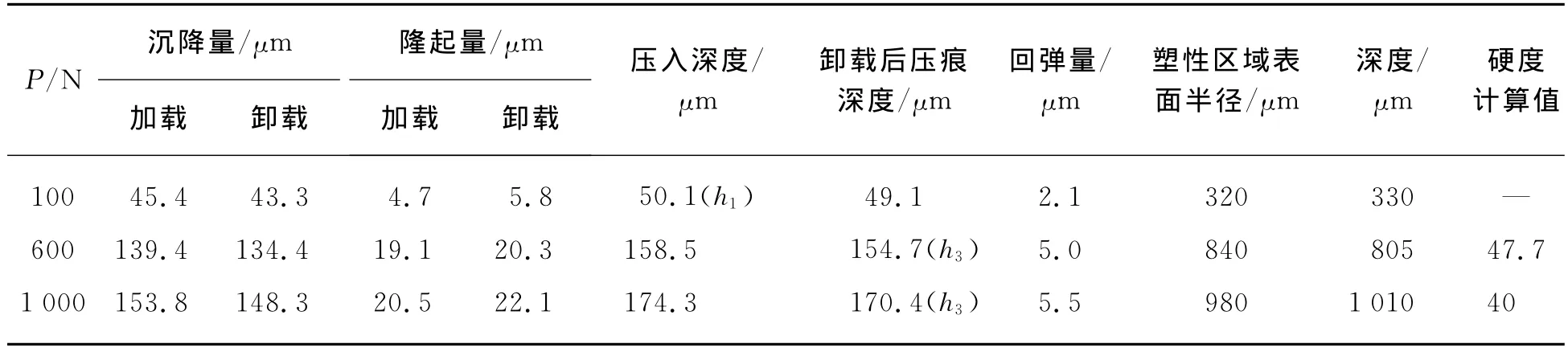
表2 圆锥压头下45钢的压入响应Tab.2 Indentation parameters under conical indenter for material 45steel

表3 圆锥压头下40Cr的压入响应Tab.3 Indentation parameters under conical indenter for material 40Cr

在此基础上，深入研究载荷作用下整个压入过程，分析具有不同残余应力试件的压入问题，获得压入深度、隆起量、回弹量、压痕深度和压痕弹塑性区域。图3为在P＝500N作用下，当残余应力分别为－400、0、400MPa时的压入响应。从图中显示数值中可直接得到：残余应力为－400MPa时压痕中心处最大压入深度为94.464μm，无应力时压入深度为1.011 97mm，残余应力为400MPa时压入深度为112.589μm。

图3 具有不同残余应力下的压痕位移量Fig.3 Indentation depth under various residual stress

通过有限元分析，得到不同载荷下残余应力与压痕深度、隆起部分、回弹量间的关系及变化规律。图4（a）反映残余应力对压痕深度的影响程度，压应力使压痕深度减少，而拉应力使压痕深度增加，但这种增加或减少的程度不大；图4（b）反映残余应力对加、卸载后回弹量的影响，压应力使弹性回复能力增加，回弹量大，h3小，h小，硬度高；拉应力使回弹能力下降，回弹量小，h3大，h大，硬度小，即说明了拉应力使材料硬度值下降，压应力使材料的硬度值提高，但下降和提高的程度不大。随着载荷的施加，压痕接触行为由弹性行为逐渐转向弹塑性行为，当接触应力达到被压材料弹性行为的极限并开始塑性流动时，塑性区域被周围保持弹性的材料所包围，当拉应力程度大时，在较大载荷作用下，被压头挤压的材料受到周围固体的弹性膨胀而调节，故减少了压头附近的堆聚形成下沉量，如图4（c）所示，在P＝1kN、拉应力大于200MPa时，出现了下沉量（负值）；当材料为压应力时，挤出的材料在塑性流动作用下自由流向压头的四周，并逐渐堆聚形成隆起量。

2.3 压痕过程中接触问题和塑性区域

图4 具有不同残余应力下压入响应Fig.4 Indentation response under various residual stress

压入过程中的接触问题包括两个接触物体受压后而产生的局部应力和变形，即接触应力与接触变形两部分［15］。接触应力具有明显的局部性质，且总是随着离开接触处距离的增大而迅速衰减，在接触表面中心处的压应力为最大。在载荷作用下，接触应力小于材料的屈服极限，则为弹性接触问题；当接触应力超过材料的屈服极限，则为弹塑性接触问题。压球与试件表面的接触问题是在载荷的作用下，试件表面产生一定的塑性变形，使之产生一定的压痕深度，在接触区域产生弹塑性接触行为。这种弹塑性接触问题与载荷大小、压球形状、材料特性有着密切的关系。在压痕实验中，无法直接观察到位于压头下试件材料经历的弹性变形、弹塑性变形以及塑性变形等不同的阶段，故采用有限元方法进行接触问题的研究，可以利用数值模拟展现材料的变化过程，分析材料在压痕周围处的应力变化及其规律，完成真实压痕试验不便完成的研究。图5给出了当P＝500N下残余应力分别为－400、0、400MPa时压痕周围等效应力的分布状况。

根据von Mises屈服准则，压痕等效应力大于材料屈服应力的区域为塑性区域，反之，为弹性区域。在理论上，塑性区域为以r为半径的核心区域，但由于残余应力的存在，塑性区域并不是以r为半径的核心区域，应力状态不同时对于塑性区域的影响有着一定的规律性，并随着载荷增加进一步促进塑性区域发展，如图6所示。

压应力的存在使表面塑性区域半径大于塑性区域深度，并随着压应力的增加而减少；拉应力的存在使表面塑性区域半径小于塑性区域深度，并随着拉应力的增大而增加，故应力的性质和大小直接影响压痕表面塑性区域，且随着载荷增加呈非线性增加。在压痕法测量构件残余应力时，需要根据塑性区域确定弹塑性边界，合理选择测量距离，安排应变片测试位置，避免受塑性行为的非线性变形，影响所测应变量与试件内应力之间的内在规律。然而，在实际的压痕法测量残余应力过程中，由于塑性区域的未知，影响应变量测试位置的确定，从而影响压痕法中测量残余应力的准确性。

3 结 论

（1）残余应力的性质和大小影响整个压入响应，残余应力为压应力时，试样表面在靠近圆锥压头处都会有堆聚现象发生，形成隆起量；而残余应力拉应力时，随着载荷的增加，由隆起量逐步为下沉量，故可采用直观法观察隆起量或下沉量判断残余应力的状况。

（2）塑性区域受残余应力影响作用较大，在残余应力测试中，由于塑性区域预先未知，影响应变量测试位置的确定，从而影响残余应力测试结果。

［1］ Lee J H，Kim T，Lee H.A study on robust indentation techniques to evaluate elastic－plastic properties of metals［J］.International Journal of Solids and Structures，2010，47（5）：647－664.

［2］ Lee Donghee，Barber J R，Thouless M D.Indentation of an elastic half space with material properties varying with depth［J］.International Journal of Engineering Science，2009，47（11－12）：1274－1283.

［3］ Le M Q.Material characterization by dual sharp indenters［J］.International Journal of Solids and Structures，2009，46（16）：2988－2998.

［4］ Baxevani E A，Giannakopoulos A E.The modified rockwell test：A new probe for mechanical properties of metals［J］.Experimental Mechanics.2009，49（3）：371－382.

［5］ Sakharova N A，Fernandes J V，Antunes J M，et al.Comparison between Berkovich，Vickers and conical indentation tests：A three－dimensional numerical simulation study［J］.International Journal of Solids and Structures，2009，46（5）：1095－1104.

［6］ 崔 航，陈怀宁，陈 静，等.球形压痕法评价材料屈服强度和应变硬化指数的有限元分析［J］.金属学报，2009，45（2）：189－194.

［7］ 胡和平，廖艳果，周益春.韧性薄膜／基底体系锥形压痕的有限元分析［J］.南华大学学报：自然科学版，2009，23（4）：56－61.

［8］ Liao Yanguo，Zhou Yichun，Huang Yongli，et al.Measuring elastic－plastic properties of thin films on elastic－plastic substrates by sharp indentation［J］.Mechanics of Materials，2009，41（3）：308－318.

［9］ Lee J H，Lee H，Hyun H C，et al.Numerical approaches and experimental verification of the conical indentation techniques for residual stress evaluation［J］.Journal of Materials Research，2010，25（11）：2212－2223.

［10］ Yan J，Karlsson A M，Chen X.Determining plastic properties of a material with residual stress by using conical indentation［J］.International Journal of Solids and Structures，2007，44 （11－12）：3720－3737.

［11］ Huber N，Munz D，Tsakmakis C.Determination of Young's modulus by spherical indentation［J］.Journal of Materials Research，1997，12 （9）：2459－2469.

［12］ Oliver W C，Pharr G M.Measurement of hardness and elastic modulus by instrumented indentation：Advances in understanding and refinements to methodology［J］.Journal of Materials Research，2004，19（1）：3－20.

［13］ Taljat B，Zacharia T，Haggag F M.Analysis of ball－indentation load－depth data：PartⅠ.Determining elastic modulus［J］.Journal of Materials Research，1997，12（4）：965－974.

［14］ Larsson P L.On the mechanical behavior at sharp indentation of materials with compressive residual stresses［J］.Materials and Design，2011，32（3）：1427－1434.

［15］ Johnson K L.接触力学［M］.徐秉业，罗学富，刘信声，等，译.北京：高等教育出版社，1992.

Conical Indentation Under Residual Stress

SUN Yuan
（School of Mechanical Engineering，Shanghai Dianji University，Shanghai 200245，China）

The finite element method is used to study indentation parameters under load，and calculate hardness.The calculated values agree well with the measurements，indicating effectiveness and reliability of the finite element analysis.Based on numerical simulation of a cone indenter，we analyze the indentation response of materials with varying residual stress，and the effect of residual stress on the indentation response.The problem arising from indentation for measuring residual stress is studied for the plastic region around indentation.The result shows that the residual stress affects indentation response in different degrees.Pile－up appears around the cone indenter due to compression stress，and sink－in appears due to tensile stress.These can be used to determine the residual stress by direct observation.Plastic region is clearly widened with tensile stress and narrowed with compression stress.The position for strain becomes uncertain in the indentation test due to unknown plastic region，which can affect the measuring results of residual stress.

residual stress；indentation response；plastic region；uncertainty position for strain

孙 渊（1968－），女，教授，博士，专业方向为机械工程，E－mail：suny＠sdju.edu.cn

TB 125

A

2095－0020（2012）03－0141－06

2012－04－15

上海市教育委员会科研创新项目资助（11YZ269）；上海市教育委员会重点学科资助（J51902）；上海电机学院科研启动经费项目资助（10C411）