毛织物的抗皱性能与其结构参数关系的探讨

郭 昕，许兰杰

(辽东学院，辽宁 丹东 118003)

影响织物抗皱性能的因素很多，例如纱线种类、结构及抗弯性能、织物的紧度、体积重量、织物组织与表面特征、厚度及后整理等。

国内外学者对织物抗皱性能与其结构参数的关系的研究做了大量的工作，取得了丰硕的成果，为织物的设计提供了理论依据。但目前的一般做法是，对影响织物服用性能的有关因素逐一进行分析，忽略了各因素之间的相互作用。为了更好地探讨织物结构与其性能之间关系，本文以毛织物为例，运用SPSS软件对织物的折皱性能与其结构参数之间的关系进行研究探讨，以期为毛纺科研人员开发与生产精纺毛织物提供一定的科学依据。

1 试验条件

1.1 试验仪器

YG541D型数字式织物折皱弹性仪、GB425-75型电子天平、YG141D型数字式织物厚度仪。

1.2 试验条件

(1)选取性能相似，有代表性的17种毛织物面料。

(2)采用相同的仪器与设备对织物的结构进行分析，测试纱线的线密度、织物的厚度、紧度、面密度及织物密度等指标。

(3)采用相同的仪器与设备测试面料的抗皱性能。

1.3 试验标准及方法

1.3.1测试标准

抗皱性根据标准GB/T3819—1997；按GB/T3820—1997测定试样厚度；按FZ/T01093—2008测定织物密度。

1.3.2试验方法

实验采用YG—541D织物折皱回复角测定仪用凸样法测试织物折皱性，测得织物受压后释去外力逐渐回复过程中在较短时间(15 s)内回复的急弹性回复角，以及在一段时间(5 min)后回复的缓弹性回复角，可评定织物的折皱弹性性能[1-3]。对于每种织物都进行了10 次测试，取每种织物经向平均值、纬向平均值后的折皱回复角作为各织物折皱弹性性能的评定，试样尺寸为40 mm ×15 mm 凸型样。计算折痕回复角的算术平均值，试验数据见表1～表4。

2 试验结果

表1～表4为织物抗皱性能的测试结果。

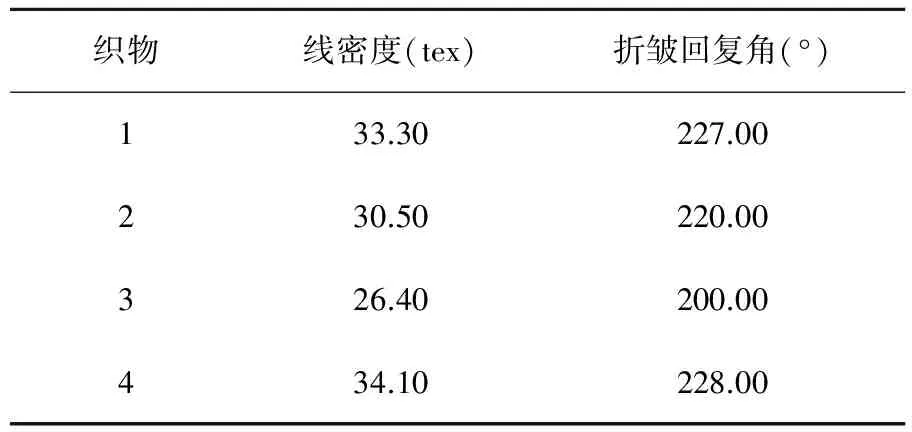
表1 不同线密度织物的折皱回复角

表2 不同厚度织物的折皱回复角

表3 不同紧度织物的折皱回复角

3 试验结果分析

针对测试结果，通过SPSS统计分析软件对织物的结构参数与折皱性能作如下回归分析：

所谓回归分析即相关分析。回归分析是假设因变量与自变量之间存在线性关系，通过确定模型参数来得到回归方程。当因变量与一个或两个以上的自变量存在线性关系时，其线性回归的数学模型为：y= ax1+ bx2+ c，本文是先研究各结构参数分别与折皱性能的相关关系，回归模型为：y= ax + b，再综合分析各结构参数对织物折皱性能的相关性，其线性回归的数学模型为：y= ax1+ bx2+cx3+ dx4+e。

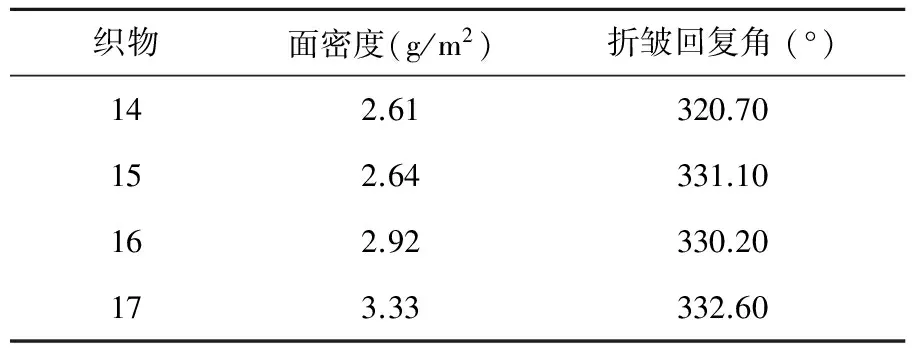
表4 不同面密度织物的折皱回复角

3.1 单一的结构参数对折皱性能的影响

折皱恢复性能是指织物受力变形，当外力解除后，织物的急弹性、缓弹性变形恢复为原来形状的能力，折皱恢复性能是衡量服装性能的重要指标[4]。

3.1.1纱线线密度与折皱性能的关系

对纱线线密度不同而其他参数相接近的试样进行分析，可得到织物折皱性与纱线线密度之间的关系曲线(见图1)及回归方程(见表5)。

图1 织物的折皱性与纱线线密度之间的关系

表5 回归方程

y = 104.619+ 3.673x (相关系数R2 = 0.966)，即织物的折皱回复角与线密度之间线性关系十分显著。在其他条件相同的情况下，线密度越大，即经纬纱号数越大，或经纬密度越大，折皱回复角越大。

3.1.2织物厚度与折皱性能的关系

对织物厚度不同而其他参数相接近的试样进行分析，可得到织物厚度与织物的折皱回复角之间的关系曲线(见图2)及回归方程(见表6)。

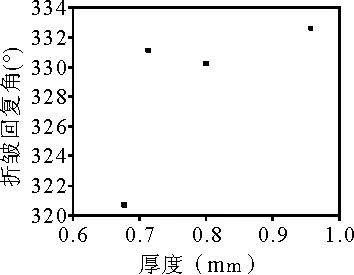
图2 织物的折皱性与织物厚度之间的关系

y =305.493 + 29.444x(相关系数R2 = 0.471)。由图2可知，折皱恢复性能随织物厚度的增加而增加。织物越厚，抗弯刚性越大，越不易起皱。薄织物比厚织物易起皱。其次，厚织物重量较大，穿着者在站立状态时，易拉平折皱；另外，织物发生折皱后的保持能力，随纤维周围空气的相对湿度和温度的变化而变化，在较厚的织物中，湿度、温度传递较慢，变化小，因此厚织物的折皱小一些[5]。

3.1.3织物紧度与折皱性能的关系

对织物紧度不同而其他参数相接近的试样进行分析，可得到织物紧度与织物的折皱回复角之间的关系曲线(见图3)及回归方程(见表7)。

y =42.152 +1.925x(相关系数R2 = 0.612)。织物的折皱恢复性能与织物的紧度有密切的关系。在一定的条件下，即品种、纱号、原料成分和织纹组织相同的情况下，织物紧度大、结构紧密、其纱线内应力大，抗弯曲压缩性能好，去除外力后恢复速度快，弹性好。

图3 织物的折皱性与织物紧度之间的关系

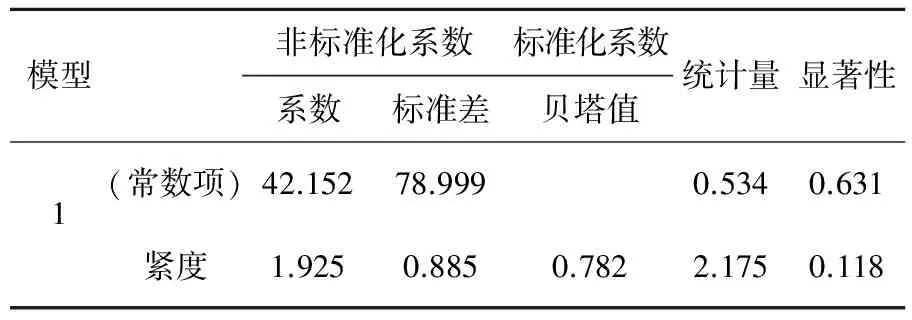
表7 回归方程

3.1.4织物面密度与折皱性能的关系

对织物面密度不同而其他参数相接近的试样进行分析，可得到织物面密度与织物的折皱回复角之间的关系曲线(见图4)及回归方程(见表8)。

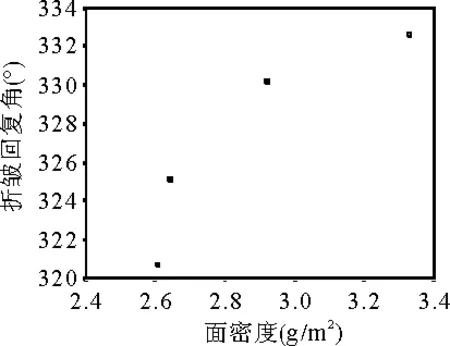
图4 织物的折皱性与织物面密度之间的关系

y=285.607+ 14.446x(相关系数R2 = 0.82)，即织物的折皱回复角与面密度之间线性关系显著。在其他条件相同的情况下，面密度越大，折皱回复角越大。

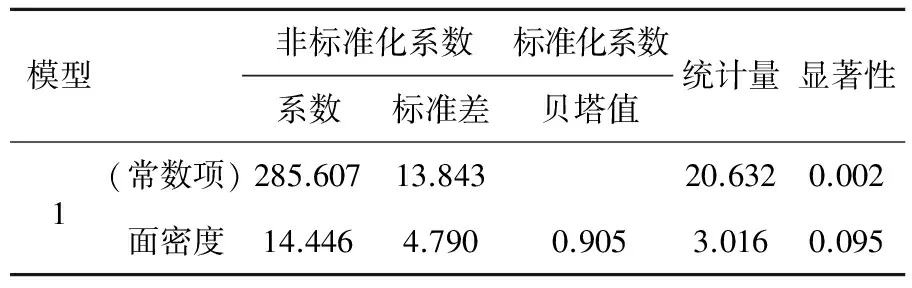
表8 回归方程

3.1.5织物密度与折皱性能的关系

织物的折皱性与经纬密度有关，适当增加经纬密度，可以提高折皱恢复性能和弹性。如斜纹织物要比相同覆盖系数的平纹织物为好。无论是急弹性回复角还是缓弹性回复角，经向回复角的平均值都小于纬向回复角，主要原因是纬向密度小于经向密度。机织物由经纱、纬纱交织而成，纱线由纤维或长丝通过加捻组成，因此，纤维之间或纱线之间的表面摩擦性能将影响它们之间的相对移动，相对移动时阻力的大小将影响纤维的受力与变形[6-7]，所以，织物的折皱性也与纤维的表面摩擦性能及纤维之间相对移动的能力有关。纬向密度低，纤维之间的摩擦力小，容易伸展，使纤维的相对移动更容易，所以回复角大。

3.2 结构参数对织物折皱性能的综合影响

通过上述单一因素对织物折皱性影响的分析和所建立的回归方程，可以看出:纱线的线密度，织物厚度，紧度以及面密度都与织物的折皱性有显著的相关关系。下面利用SPSS软件进行多元线性回归分析。输出结果如表9～表12所示。

表9 模型概要

注：a.预测变量: (常量), 面密度；

b.预测变量: (常量), 面密度, 线密度。

表9结果说明需要建立两个回归模型。

模型1：首先把面密度选入自变量，R方为0.775，是面密度在织物折皱性总变动中的影响比率，即织物折皱性的变动中有77.5%是受织物面密度的影响。

模型2：在模型1基础上，将线密度追加选入自变量，R方为0.903，说明织物的折皱性变动中有90.3%是受织物面密度和纱线线密度的共同影响，即实际上影响比率只增加12.8%，即引入线密度对织物折皱性影响不大。随着自变量的增加，调整的R方不断提高，回归方程的估计标准误差不断减小。

表10 方差

注：a.预测变量: (常量), 面密度; b.预测变量: (常量), 面密度, 线密度; c.因变量: 折皱回复角。

表10结果说明：表中两个模型的方差情况。第二列分别是回归平方和、剩余平方和、因变量的总平方和；第四列分别是平均的回归平方和、平均的剩余平方和。随着自变量的引入，均方误差不断减小，说明这些自变量的确为解释因变量做出了贡献。

从模型1看，验证回归式显著性的F统计量值是30.938，Sig.=0.000<0.001，即显著符号是“* * *”，所以由面密度一个自变量构成的回归式统计上是非常显著的。

从模型2看，验证回归式显著性的F统计量值是37.431，Sig.=0.000<0.001，即显著符号是“* * *”，所以由面密度和线密度两个自变量构成的回归式统计上也是非常显著的。

表11结果说明：第一列是回归过程中引入自变量的情况，第二列是对应的回归系数，根据这个回归系数可得回归方程。第四列是标准化回归系数，可以衡量自变量对因变量的贡献程度，根据标准化回归系数，最终可得标准化回归方程：y=176.626-0.396x1+4.179x2。其中y为折皱回复角，x1为织物面密度，x2为线密度。可见织物面密度对织物折皱性起了较主要的作用。

模型1：引入一个自变量“面密度”，回归常数是320.948，Sig.F=0.000<0.001，是十分显著的；回归系数是-0.511，Sig.F=0.000<0.001，是十分显著的。因此第一步回归式可以用y(折皱回复角)=320.948-0.511x(面密度)表示。

模型2：引入两个自变量“面密度、线密度”，回归式是y(折皱回复角)=176.626-0.396x1(紧度)+4.179x2(线密度)。

多元回归分析中，如果自变量引入较少，回归方程将无法很好地解释说明因变量的变化，但自变量的个数越多，由于自变量间的共线性，会给回归方程带来许多影响。如织物紧度、厚度统计上没有显著性，因而表7～表11没有加入它们，未引入方程的自变量见表12。

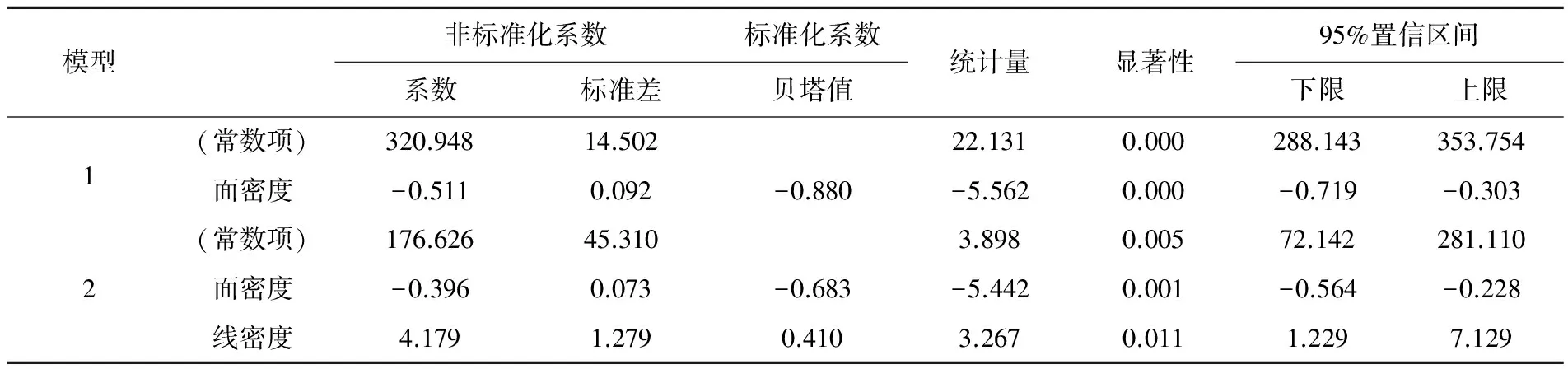
表11 回归方程

注：a.因变量: 折皱回复角。

表12 未引入方程的自变量

注：a.预测变量: (常量), 面密度; b.预测变量: (常量), 面密度, 线密度; c.因变量: 折皱回复角。

表12结果说明：回归分析过程中尚未引入方程的自变量情况。

从模型1看，线密度、厚度、紧度均未引入方程，第五列是在控制了方程中已有自变量的前提下计算出某自变量与因变量的偏相关系数，线密度的偏相关系数最高为0.756，可判定下一步它进入方程。这与模型2相吻合。第六列是自变量共线性检测中的自变量容忍度，容忍度越大，说明与其他自变量的相关关系越弱，共线性越小。从表12可看出厚度的容忍度最大，说明它与其他自变量的相关关系最弱。

从模型2看，织物紧度、厚度未引入方程，它们的偏相关系数都相当小，没有统计显著性。即使把它们追加引入，回归式的影响比率改善的部分也非常小。因此多重回归分析到此为止。

从上面的分析不难发现，在上述众多结构参数中，织物面密度和纱线线密度对织物折皱性的影响最为突出。

综合以上试验数据认为，抗皱性受织物面密度的影响最显著,其次为纱线线密度、厚度、总紧度，而受经纬密度影响较小。对某一纤维材料而言，纱线的细度、织物组织结构对织物厚度的影响，进而也影响织物的折皱性。线密度越小，织物的抗弯度越小，表现为轻薄、稀松、柔软，织物的弹性回复性较差。织物单位面积质量、厚度大,抗弯刚度较大，其抗皱性能较好。同时,织物的折皱恢复性能与织物的紧度也有密切的关系。在一定条件下，即品种、原料成分和组织相同的情况下，织物紧度大，结构紧密，其纱线内应力大，抗弯曲压缩性能好，去除外力后恢复速度快，弹性好；但当织物紧度达到一定程度时，则织物变得硬板，折皱恢复性能反而下降[8-11]。纱线弯曲程度越大，织物越丰满厚实，弹性和抗折皱性能也越好。

4 结论

本文通过对样品的测试和回归分析，探讨毛织物的折皱性能与其结构参数有较大的相关性，运用SPSS统计分析软件对织物的结构参数和服用性能指标的相关性作了回归分析，从理论上建立了织物的抗皱性能与其结构参数的关系式。

4.1抗皱性受织物面密度的影响最显著，其次为纱线线密度、厚度、总紧度，而受经纬密度影响较小。

4.2织物抗皱性能与其结构参数的关系可用y=176.626-0.396x1+4.179x2表示。其中y为折皱回复角，x1为织物面密度，x2为线密度。可见织物面密度对织物折皱性起了较主要的作用。

4.3对织物进行设计时，保持其它变量相似，改变其自变量，在一定程度上可以改善织物的某些性能。

但是实验也存在不足之处，由于各种织物的结构要求相似，其性能才具备可比性，所以选择的织物的结构参数未必那么精确，因此，利用回归分析的方法找出各结构参数对服用性能影响的显著性从而得到共性的结论，与真实存在一些误差。

参考文献：

[1] 徐蕴燕.织物性能与检验(2版)[M].北京:中国纺织出版社，2004.

[2] 赵书经.纺织材料实验教程[M].北京:中国纺织出版社，2000.

[3] 姚穆.纺织材料学(3版)[M].北京:中国纺织出版社，2009.

[4] 王锦成,刘海波.毛精纺产品结构与折皱恢复性能的关系[J].上海纺织科技，1999,27(4):60—61.

[5] 于学智,吴世刚,王漓江.柞丝绸厚度与抗皱性相关程度的回归分析[J].辽东学院学报，2007,14(3):173—175.

[6] 姜为青.薄型精纺毛织物综合服用性能与结构参数的关系[J].纺织学报，2006,27(11):86—89.

[7] 李梅,张会青.毛织物的服用性能与纱线和织物结构的关系[J].毛纺科技，2005,(6):32—34.

[8] 张晓婷,高卫东,卢雨正.织物折皱回复角与其物理力学性能的关系[J].纺织学报，2008,29(6):29—31.

[9] 赵丽丽，张金瑞，徐锡方，等.轻薄型精纺毛织物与衬料的互配性研究[J].山东纺织科技，2004，45(3)：4—6.

[10] 谢英，杨利永，沈宋，等.防紫外与凉爽性精纺毛织物产品开发[J].山东纺织科技，2008，49(2)：17—19.

[11] 冯建永，段亚峰，张龙江，等.T/R纺毛织物的生产工艺研究[J].山东纺织科技，2008，49(6)：15—18.