多尺度有限元建模及在结构设计中的应用

黄银燊，袁理明，吕 鹏

(中南建筑设计院股份有限公司，湖北武汉430071)

随着我国经济的迅速发展，对建筑结构的功能要求日趋复杂，外观要求也更加苛刻，这给工程结构设计带来了巨大的挑战，结构工程的设计分析也经历一个迅速发展的阶段。一些新的结构形式和结构设计理念不断提出。精细化分析、精细化设计是目前的趋势。对于大型的结构一般采用杆系模型、壳、墙等宏观模型分析结构的整体性能，但是这些模型不能准确模拟结构局部细节的信息，如复杂构件局部应力分布、节点半刚性、节点破坏形态等。对大型结构进行整体精细化实体建模分析，由于计算机条件限制且工作量巨大，是不现实的。因此对关键的构件局部和节点的分析，通常的处理方法是将其从宏观模型中取出，单独进行精细化的有限元分析，考虑更多的结构细节，如考虑接触、材料非线性等，为结构设计提供依据。然而，这种二次分析难以准确确定局部模型的边界条件及其具体的加载形式，而不同的边界条件对分析的结果影响很大，给判断分析结果带来困难［1-2］。而且在往复荷载的作用下，难以判断局部模型的最不利工况，需要进行多次不同工况组合下的分析。

而在统一的模型下进行结构的多尺度建模计算为上述问题的解决提供了有效的解决方案［3-4］。多尺度计算的应用领域非常广泛，而对于工程结构而言，多尺度主要考虑采用宏观与微观模型相结合的模型，兼顾整体和细部，目前在大跨度桥梁结构分析中应用较多。对于大型结构整体而言，其单元尺寸往往在101m级，而对于细部而言，其特征单元尺寸一般在mm级。结构的多尺度模型首要问题就是解决不同量级尺度下模型的联接问题，使整体结构的分析和局部细节的分析同步进行，并且考虑到结构材料的局部微细观尺度上的损伤演化与整体结构之间的相互影响。

本文探讨了在ANSYS软件中进行了结构多尺度建模计算的方法，验证了微观模型和宏观模型之间联接的准确性，并在一复杂超限高层组合结构的设计中进行了包括复杂节点微观模型和整体结构模型的多尺度弹塑性时程分析。计算结果表明，多尺度模型可以更准确地模拟结构热点部位的受力情况，为设计人员对结构性能的把握提供更加丰富的信息。

1 多尺度有限元建模

1.1 界面联接方式

从工程结构设计角度出发，多尺度建模首先需要根据节点的复杂程度和破坏过程中的非线性程度，选择适当尺度的分析模型。图1为精细模型与宏观模型的联接示意图。实际工程中常见的模型组合包括：梁单元与实体(壳)单元联接、壳单元与实体单元联接等［5］。由于不同单元模型采用的力学简化和假设不同，故需要在不同精度模型之间采取适当的联接方式，达到力的平衡和变形的协调，并且尽量不造成对模型的过分约束。以精细模型为实体单元、宏观模型为壳单元的联接来讲(剖面如图1)，恰当的联接方式应该是，变形后的实体单元和壳单元交界面上各点位移贴合，但是在交界面上各点位移沿平行于该面方向的分量则不能一致。模型界面间转动自由度的传递按照平截面假定。其位移协调条件可以表示为：

其中为θ2'点的转角，t为单元厚度。

ANSYS中提供了多种方式进行不同精度单元之间的联接。一种简单的方式是，在局部坐标系下将上述条件直接写成约束方程形式;另外一种方式是对界面处适当的自由度建立刚性联接(REB2)，在界面区域自动形成约束方程，从节点的位移与主节点始终保持一致，但会导致刚度的增加。上述两种方式可用于小变形分析。对于大变形问题，ANSYS中提供用多点约束(MPC)方法来进行各不同精度模型的耦合，即用接触算法来模拟体耦合。这种方法能更好地模拟真实情况，而且使用范围更广。MPC方法可以克服传统接触算法和ANSYS中的其他多点约束工具的缺点，不需要输入接触刚度。对于小变形问题，它代表真实的线性接触行为，求解系统方程时不需要平衡迭代。对于大变形问题，MPC方程在每个平衡迭代中不断进行更新，克服了小应变的限制条件。在实际工程中应根据分析目的、模型复杂程度和计算代价等条件选择适当的约束方法。

图1 不同尺度模型联接

1.2 联接方法算例

在ANSYS软件中用一个长度为3 m的悬臂矩形钢梁模型的压弯加载算例验证了上述多尺度建模方法的可行性。矩形钢管梁截面高度为500 mm，宽度350 mm，钢管壁厚为10 mm。材料应力应变关系采用双折线模型，初始弹性模量为200 GPa，屈服后硬化模量为3 GPa。建立了4个有限元模型(如图2)：A模型全部采用壳单元shell181;B模型和C模型均采用多尺度模型，多尺度模型一段采用壳单元shell181，另一段采用梁单元Beam189，界面位置不同(B和C的粱单元分别长0.6 m和1.5 m)，并采用MPC多点约束界面联接方法;D模型全部采用梁单元Beam189建模。

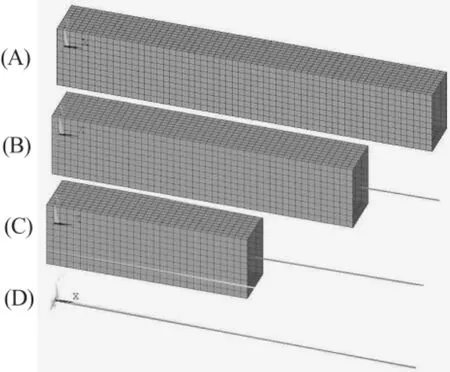
图2 验证模型

加载过程如下：首先在悬臂端沿轴向施加恒定轴压力20 kN，然后在垂直于梁轴线方向施加竖向荷载P。得到P(竖向荷载)—Δ(顶点位移)曲线，如图3所示。可见A、B、C三种模型曲线基本完全吻合，而D模型荷载偏小，但结果相差在3%以内，对于工程分析可以忽略。图4给出了各模型的等效应力云图，可以看出，多尺度模型B和C壳单元部分的应力分布与A模型吻合较好，在联接处没有出现应力集中情况，且保持了变形的协调。仍然采用上述模型，进一步进行了弹塑性动力分析验证。在悬臂梁的端部添加质量，并考虑钢梁自身重量，体系阻尼比0.04。输入单向El Centro NS地震波，分析得到各模型的悬臂端位移反应(Δ)时程曲线，如图5所示，并与理论计算结果进行了比较。可见各模型的位移反应时程曲线吻合亦令人满意，位移反应最大值相差在3%以内。

图3 P—Δ曲线

图4 等效应力/Pa

图5 动力分析结果比较

2 工程应用

在实际工程结构整体分析中，大多采用基于梁、壳、墙模型等宏观模型进行整体结构非线性有限元计算。采用梁单元建立的模型，在节点部位被简化为刚性，结构的破坏主要体现为梁柱构件的塑性铰，而实际上节点本身的破坏在震害中并不少见，“强柱弱梁、节点更强”的设计往往难以实现，且不能经受实际地震的考验［6］。一般来说，节点部位构造复杂，采用常规的计算方法难以准确得到应力分布、破坏形态等。为了解决上述问题，在一复杂超限连体高层结构设计中，对多个关键节点和热点部位采用实体单元或壳单元精细建模，并进行了弹塑性动力时程分析。

2.1 结构模型

该结构为由两栋高度不同的塔楼组成的高位连体复杂高层结构，高层塔楼均采用“圆钢管混凝土柱+H型钢梁或钢桁架+钢筋混凝土核心筒”结构，连接体采用钢桁架结构。结构主楼和副楼混凝土核心筒均偏置。本结构同时具有扭转不规则、凹凸不规则、局部夹层、楼板不连续、部分楼层刚度突变、部分楼层承载力突变等超限内容。结构总层数46层，总高度约210 m，整体模型如图6(a)所示。

连接体桁架设计是本工程设计的关键，而其中节点的构造和处理尤为重要。连接体弦杆在多种工况组合下为压弯或拉弯构件，采用方箱型截面，截面尺寸均为500 mm，最大板厚40 mm。腹杆均采用倒置的 H型钢度高为500 mm，翼缘宽度500—700 mm，最大板厚60 mm。钢材选用Q345GJC。在节点中，杆件轴力通过翼缘直接传至节点板，各轴力汇交于节点板取得平衡。本文选取其中构造最复杂的两个关键节点进行了多尺度的有限元分析。

节点1为连接体主钢桁架下端与主楼筒体墙体连接部位，桁架弦杆延伸入剪力墙筒体内，墙内设有钢骨柱，如图6(b)所示。节点2为连体主桁架中部一复杂钢节点，如图6(c)所示。整体模型中用Beam188和 Beam189单元模拟结构杆件，用shell181单元模拟墙体，shell63单元模拟楼板;精细模型中，节点1采用实体单元模拟钢构件和混凝土，节点2采用弹塑性壳单元模拟钢板，并植入整体模型中。

图6 多尺度结构模型

2.2 分析结果

本文共进行了两条天然波和一条人工波的大震工况的分析，采用了精细模型分析，时间稍有增加。图7为节点1某时刻的混凝土竖向应力云图。由图7可见，混凝土在与加劲板接触处压应力较大，Z向应力超过设计强度，此处混凝土应该合理设计。另外可以发现，节点处钢材在大震下均未进入塑性状态，但是连接钢板转角处局部应力水平偏高。

图7 节点1混凝土竖向应力云图(kPa)

图8给出了节点2应力较大时的应力应变图。分析表明，在大震作用下整个节点大部分都处在较低的应力水平下，而只在某些小范围局部应力较高甚至进入塑性，但这种局部高应力范围较小，会随着施工焊接的的影响而缓解，或者通过应力重分布而缓解，对结构整体的影响不大。

图8 节点2 Mises应力(Pa)

图9 节点5号杆件2两种模型杆件轴力时程比较

图9给出了节点2的5号杆件在整体模型和精细模型在各时刻的杆件内力对比。由图9可见，两个模型计算出的杆件轴力基本上完全吻合，因为对于多尺度的精细模型来说，节点的边界条件在各个时刻和各个工况下都是天然满足的。采用精细化的模型可以更精确地得到各个时刻的节点应力分布，为节点的设计提供有力依据。

4 结论

3.1 在ANSYS中验证了不同尺度之间单元的联接方式，表明可以实现不同尺度模型间的联接过渡，误差均在在工程可接受范围之内。

3.2 在一复杂混合高层结构分析中进行了结构多尺度计算，通过不同尺度单元间的协同，实现了复杂节点微观模型和整体框架模型的多尺度弹塑性时程计算，计算结果表明，多尺度模型可以更加准确地模拟节点的实际受力情况。

3.3 多尺度有限元计算方法可以在可接受的计算资源和计算时间下，既反应结构的整体性能，又反映结构的局部信息，在结构设计的领域有着较好的应用前景。

［1］ 郑伯兴，黄长华.钢管相贯节点疑难问题分析及对策探讨［J］.钢结构，2007，22(9)：91-94.

［2］ 陈其业，梁乃刚.多分支管节点的有限元分析［A］.见：中国钢结构协会海洋钢结构专业委员会，第一次学术交流论文集.1985.

［3］ 吴佰建，李兆霞，汤可可.大型土木结构多尺度模拟与损伤分析——从材料多尺度到结构多尺度力学［J］.力学进展，2007，37(3)：321-336.

［4］ 陆新征，林旭川，叶列平.多尺度有限元建模方法及其应用［J］.华中科技大学学报(城市科学版)，2008，25(4)：76 ～80.

［5］ 王勖成，邵敏.有限元方法基本原理与数值方法［M］.北京：清华大学出版社，1988年.

［6］ 夏珊，刘爱文.汶川地震框架柱震害的初步分析［J］.震灾防御技术，2008，3(3)：237-242.