在工程应用中i p-i q谐波检测算法改进与仿真研究

张俊敏，玉振明

（1.桂林电子科技大学 信息与通信学院，广西 桂林 541004；

2.梧州学院 信号分析与处理实验室，广西 梧州 543002）

在工程应用中i p-i q谐波检测算法改进与仿真研究

张俊敏1，玉振明2

（1.桂林电子科技大学 信息与通信学院，广西 桂林 541004；

2.梧州学院 信号分析与处理实验室，广西 梧州 543002）

谐波检测是有源电力滤波器非常关键的一环，只有准确地检测到谐波才能进行合理补偿。为了克服有源电力滤波器中ip-iq算法补偿效果在电网波动和负载变化时出现下降的不足，提出了一种改进的ip-iq谐波及无功电流检测方法，在寻找某一小频率范围内的最优滤波器的基础上，根据电网和负载变化以及模糊隶属函数进行实时投切。该算法提高了补偿后的稳态响应。改进后的算法在工程应用中具有很强的帮助作用。通过simulink仿真证明方法的有效性。

瞬时无功理论；谐波检测；有源电力滤波器；simulink

1 引言

面对电力系统的无功及谐波问题日趋严重的状况，传统的各种无功补偿及谐波抑制方法已难以满足现代电力系统的需要。作为一种新型的补偿装置，有源电力滤波器 （Active Power Filter：APF）能够快速地对大小和频率都不规律变化的谐波及无功进行补偿，近年来受到了国家和企业的广泛重视。

APF的关键技术在于谐波电流的检测与补偿电流的产生。目前电力有源滤波器中关于谐波检测的方法主要有基于FFT处理的算法、小波变换法、基于人工神经网络以及基于瞬时无功功率的p-q和ip-iq等方法。由于FFT变换法至少需要一个工频周期，因此延迟较大。小波变换则比较复杂，延迟比较大，目前应用不广。神经网络这样的智能算法，若要满足实际效果，其结构比较复杂，目前以实验室研究为主，应用也不广。而基于瞬时无功的ip-iq方法，在滤波器设计合理的情况下，一方面因为延迟较小，另一方面实现起来也相对简单，所以目前应用最广。但在实际应用中，电网与负载的波动对ip-iq检测算法的效果有较大的影响。本研究在介绍基于瞬时无功功率的ip-iq检测算法的基础上，对现有的算法在电网与负载波动的情况下，固定的滤波器参数无法保证达到最佳的滤波效果进行研究。通过分析实验数据，找出滤波器参数与实际应用的对应关系，对ip-iq算法做进一步的改进，使之在应用中效果更佳。

2 传统瞬时无功理论的i p-i q谐波检测算法

基于瞬时无功理论[1]的谐波算法有多种，如：p-q算法、d-q算法、改进的p-q算法、p-q-r算法。关于这些基于瞬时无功功率方法实验效果的评估，文献 [2]的作者进行了系统研究。p-q算法可以说是比较优秀的。p-q算法与ip-iq算法类似，唯一不同的是：p-q算法需要检测三相电压信号，而ip-iq算法只需检测A相电压的相位即可。ip-iq算法的原理图如图1所示。

图中，C32为三相变两相变换矩阵，C23为C32矩阵的转置，C为由正余弦信号形成的矩阵。分别如下所示：

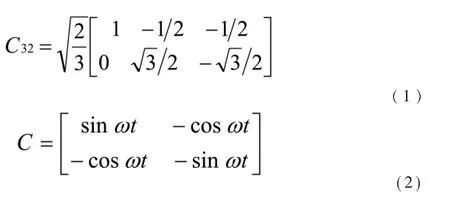
在传统算法中计算用到的正弦、余弦信号要与A相电压同相，同频率。下面可以证明：在电网电压波动与本地产生的正余弦信号的频率相位不完全一致的情况下，也可以精确地检测出电网信号。

设三相被检测电流分别为

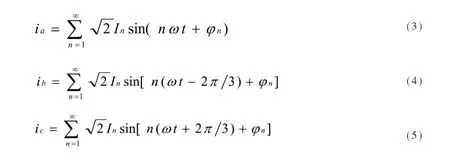
设用于计算的正弦与余弦信号分别为：sin（ωt+θ）、cos（ωt+θ）。其中ω1与电流信号频率ω不一致，相位θ为任意值。根据ip-iq算法运算规则，由图1可得：

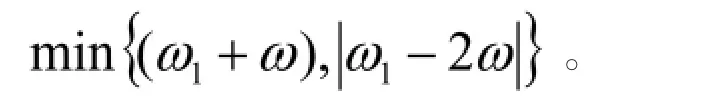
现在对得到的低频分量ip，iq，进行反变换，由图1可得

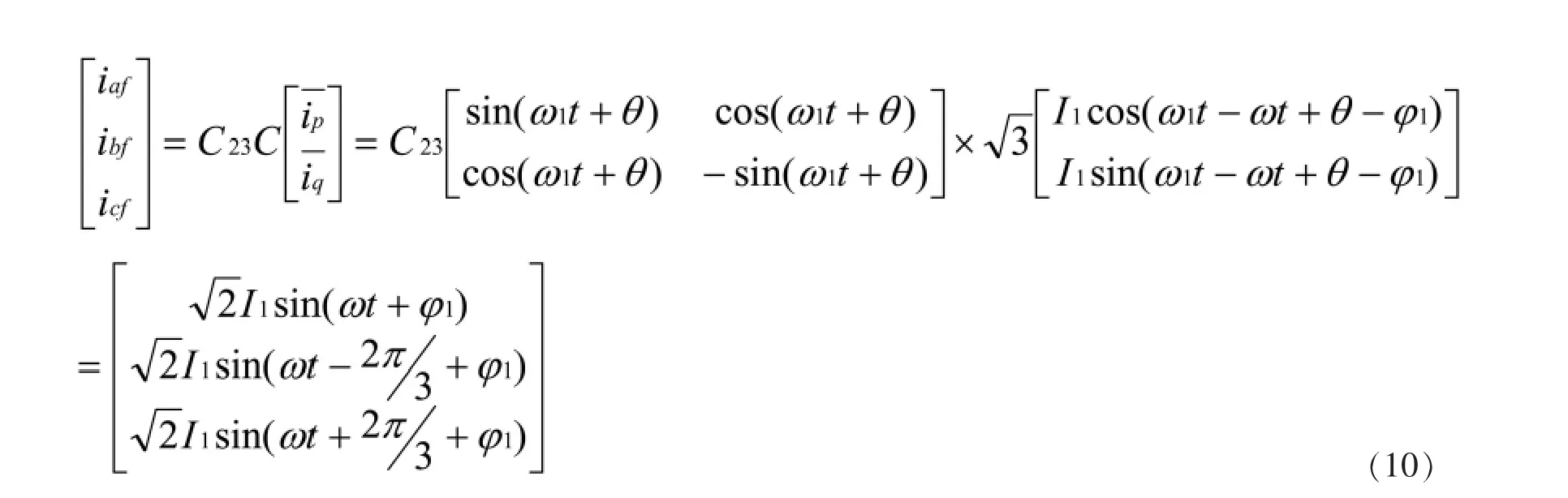
从最后的结果可以发现：尽管正余弦信号与电网电压信号的频率、相位有差别，但如果能设计出合理的低通滤波器，仍能完美地检测出谐波电流中的基波，准确地得到需要的检测信号。

3 改进的i p-i q谐波检测算法的实现原理及步骤

基于传统瞬时无功功率理论的谐波检测算法，要求变换中使用的正余弦信号与电网电压信号的频率一致，这个条件很苛刻，如果使用固定频率的低通滤波器，由于控制器存在延迟时间，所以会引起谐波检测的误差，使得补偿效果变差，甚至在某些高次谐波上有放大谐波的可能。在上一节的证明可以看出：尽管检测算法中正弦信号与电网电压信号的频率、相位存在差别，如果能设计出可跟随电网频率变化的滤波器，就能完美地检测出电流中的基波成分。

针对这一问题，大量学者对设计合理的低通滤波器做了研究，如：文献 [3]的作者提出对IIR数字滤波器与均值滤波器串联的方式进行设计。该算法提高了ip-iq算法的暂态响应，但稳态响应并未得到提高。文献 [4]的作者使用变步长的LMS的自适应滤波器代替了传统算法中IIR数字低通滤波器。该算法使暂态响应和稳态响应均未得到提高，但提高了系统的适应能力。在实验中发现：最优滤波器在某个频率范围内是唯一的，只需找出对应的最优滤波器，建立模糊集合，利用专家经验法设计隶属函数，进行实时选择投切即可。

模糊集合A为已经设计的低通滤波器，为了说明问题，选择截止频率分别为4Hz，8Hz，12Hz，16Hz， 20Hz的IIR数字低通滤波器。 μA（u） 为集合A的隶属函数， 设定取阈值为 λ1、 λ2、 λ3、 λ4、 λ5。

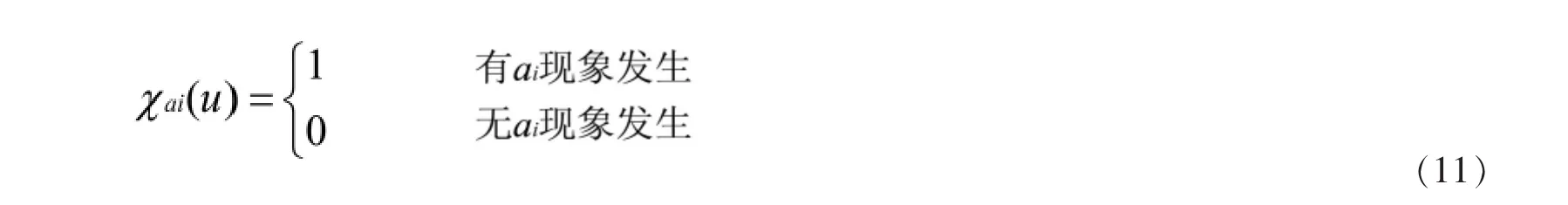
目前定义各现象a1为电网电压频率升高，a2为负载电流增大，a3为IGBT正常工作，a4为THD值降低。a1、a2、a3、a4根据实际工程测量进行 “学习”和实践检验逐步修改完善，根据式 （12）可以计算出μA（u），由μA（u）落在对应阈值区域即可实现投切。

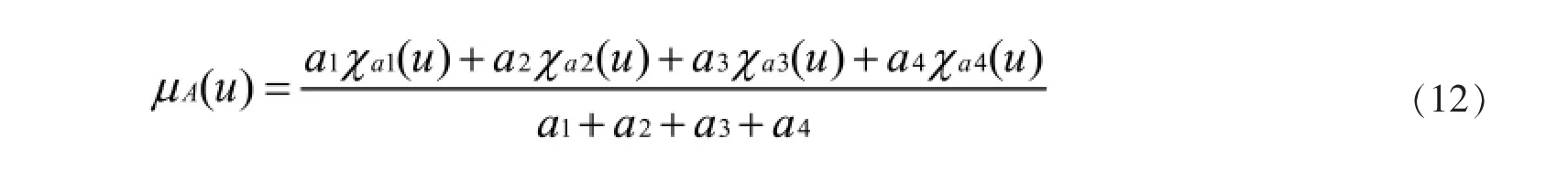
以上是本文提出的基于最优滤波器投切的谐波检测算法。在提高稳态响应的同时，增加了系统的适应能力。为了使本文所提出的算法更具有工程参考价值，在寻找最优滤波器的时候，将控制器的延迟一起考虑进去，综合评估本检测算法，实验步骤如下：

（1）使用传统ip-iq算法与滞环控制器搭建仿真实验平台；

（2）设计一组截止频率为4Hz，8Hz，12Hz，16Hz，20Hz，原型滤波器为ButterWorth的IIR低通滤波器[5]。在标准额定电压的基础上，让电网电压频率在 （50±50）Hz的范围内波动，记录下对应电压频率下的谐波总畸变率 （THD）；

（3）使用FFT分析一个工频周期的频率，根据式 （12）以实现最优滤波器的投切。

上述方法能够并行地检测谐波电流，提高谐波电流高次补偿效果，并能合理应对电网电压频率波动的情况。

4 基于Matlab的仿真实验

4.1 仿真环境建立

Matlab是一款功能非常强大的科学计算软件工具，Simulink是Matlab内一种图形化模型输入仿真工具。Simulink内含有不同的模块可供使用，为仿真提供了极大的方便。这里以simPowersystems工具箱为基础，建立的仿真模型如图2所示。

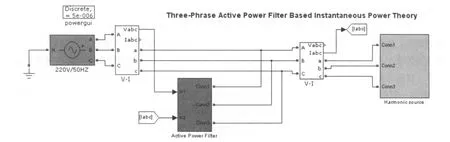
图2 谐波仿真图

图2为一个有源电力滤波器的典型补偿结构，Active Power Filter模块中，检测谐波部分使用的是ipiq算法，如图3所示。

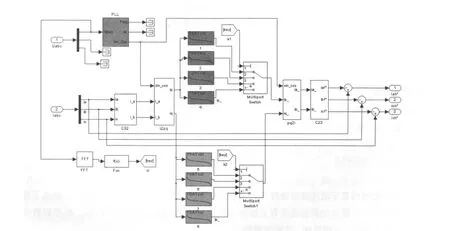
图3 谐波ip-iq检测仿真图

4.2 实验结果及分析

4.2.1 实验结果

现设定电网信号频率设为50Hz，IIR滤波器使用3阶，分析补偿后谐波总畸变率 （THD），可以得出电网电压频率50Hz下的IIR滤波器截止频率与THD的关系图 （见图4）。

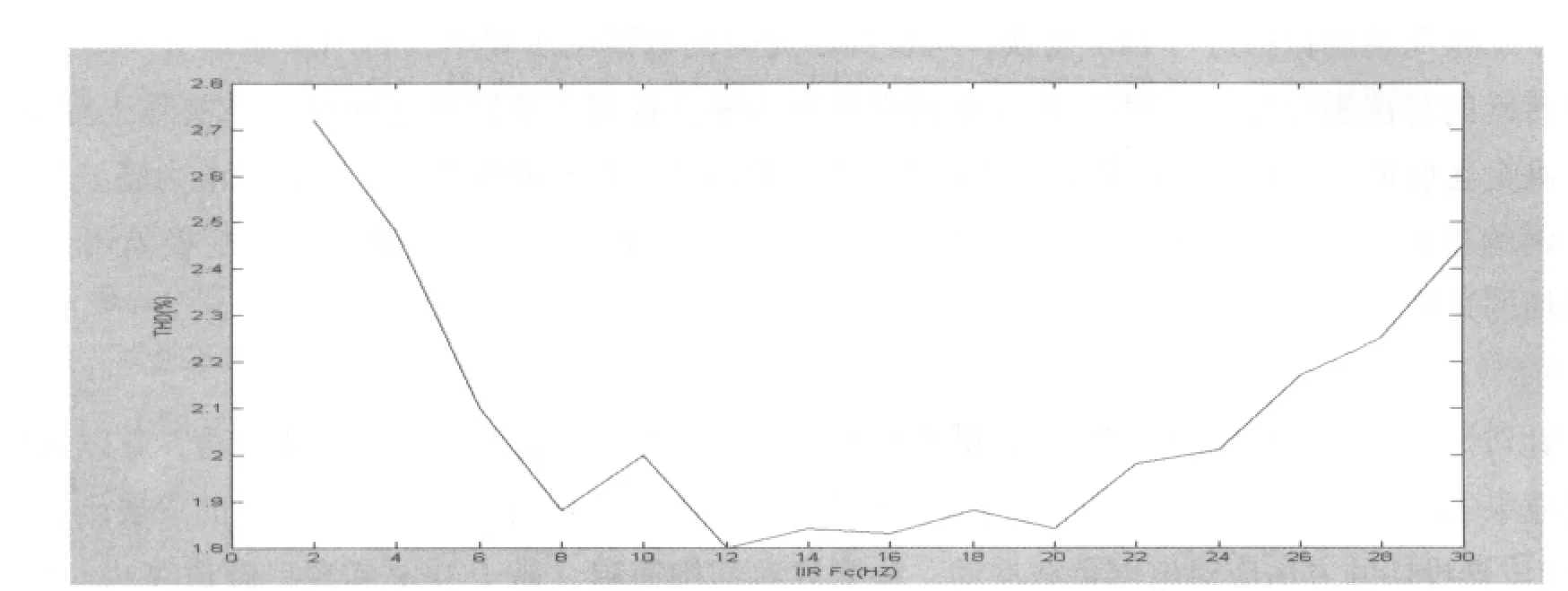
图4 电网电压频率50Hz下的IIR滤波器截止频率与THD的关系图

其中X轴为IIR数字滤波器的截止频率，变量范围是0.5Hz到30Hz；Y轴为谐波总畸变率 （THD），变量范围是1.8%到2.8%。将电网电压频率从49.5Hz变化到50.5Hz，每0.1Hz可以得到一幅图，将所有所得的图进行整理，可以得出电网电压频率 （50±0.5）Hz情况下IIR滤波器截止频率与THD的关系图（见图 5）。

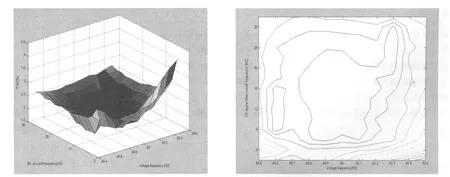
其中图5中左图，X轴为电网电压频率，变量范围是（50±0.5）Hz；Y轴是IIR数字滤波器截止频率，变量范围是0.5Hz到30Hz；Z轴是谐波总畸变率 （THD），变量范围是1.5%到4.5%。图5中右图为左图对应的等高图，X轴为电网电压频率，变量范围是 （50±0.5）Hz；Y轴是IIR数字滤波器截止频率，变量范围是0.5Hz到30Hz。

4.2.2 实验结果分析

图5中右图为左图所对应的等高图，X轴为电网电压频率，变量范围是 （50±0.5）Hz；Y轴是IIR数字滤波器截止频率，变量范围是0.5Hz到30Hz。IIR数字滤波器的截止频率最佳值以穿过等高图内环的线段长度最长为佳。如电网电压频率在49.7Hz附近波动时，截止频率12Hz为佳；电网电压频率在50Hz附近波动时，截止频率16Hz为佳；电网电压频率在50.2Hz附近波动时，截止频率20Hz为佳；电网电压频率在50.4Hz附近波动时，截止频率为24Hz为佳。

对一个工频周期的数据进行FFT变换，可检测出此时的电网电压频率，利用隶属函数实现自动投切的方式对传统的算法进行改进，使得THD维持在最低水平，提高了算法的适应性。在实际工程应用中，良好的人机交互也是必要的。一般需在液晶屏显示的内容包括：谐波补偿的效果，有源电力滤波器的工作状态及电网的当前状况等三方面。从这个角度上说，对一个工频周期的数据进行FFT变换就可以认为是不额外添加的开销。

5 结论

本文针对传统基于瞬时无功功率ip-iq谐波电流检测算法无法跟随电网以及负载波动，难以达到最佳谐波补偿效果的问题，提出了一种改进的谐波检测算法。改进算法利用专家经验法设计的隶属函数对数字IIR低通滤波器投切的方法应对电网负载波动。检测算法结构简单，易于DSP实现。改进算法与传统ipiq算法相比，在不降低动态响应的情况下，提高了检测精度且具有自适应算法鲁棒性较强的优点，仿真结果证明了改进型谐波电流检测算法的有效性。

[1]Akgai H，Kanazawa Y，Nahae A．Instantaneous reactive power compensators comprising switching devices without energy storage componets[J]．IEEE Transctions on Industry Application1984（3）：625—630．

[2]Reyes S.Herrera,Patricio Salmerón.Instantaneous Reactive Power Theory Applied to Active Power Filter Compensation：Different Approaches,Assessment,and Experimental Results[J].IEEE Transctions on Industry Electronics,2008（55）：184-196.

[3]周柯，罗安.一种改进的ip-iq谐波检测方法及数字低通滤波器的优化设计[J].中国电机工程学报,2007（34）：96-101.

[4]刘金泉，陈兆岭.一种改进ip-iq谐波电流检测算法[J].电测与仪表,2011（5）：14-17.

[5]罗安.电网谐波治理和无功补偿技术及设备[M].北京：中国电力出版社,2006：52-56.

Improvement and Simulation of the Ip-iq Harmonic Detection Method in Engineering Application

Zhang Junmin1, Yu Zhenming2
（1.Information&Communication College,Guilin University of Electronic Technology,Guilin 541004,China； 2.Wuzhou University,Wuzhou 543002,China）

The harmonic detection is crucial to the active power filter because its accuracy is the prerequisite for correct compensation.To avoid the instable ip-iq harmonic detection in the active power filter caused by fluctuating power grid and load,the paper proposes an improved detection method of ip-iq harmonic and reactive currents in which real-time switching is implemented according to the variation in power grid and load as well as the fuzzy membership functions after the optimal filter within a small frequency range is found.With its effectiveness proved by simulation of simulink,the method improves the steady-state response after the harmonic compensation and will be of enormous value in engineering application.

instantaneous reactive power theory； harmonic detection； active power filter,simulin

广西科学研究与技术开发计划项目（桂科攻10123010－13）；广西教育厅科研项目（桂教科研200911MS231）

O441.5

A

1673-8535（2012）01-0052-07

2011-12-06

张俊敏 （1985-），男，广西柳州人，桂林电子科技大学信号与信息处理专业硕士研究生，研究方向： 智能信号处理。

玉振明 （1963-），男，广西梧州人，梧州学院教授，博士，硕士生导师，研究方向：图像处理、信号处理。

覃华巧）