基于高斯分布估计的快速水平集分割方法研究

张思维

（黄淮学院 电子科学与工程系，河南 驻马店 463000）

基于高斯分布估计的快速水平集分割方法研究

张思维

（黄淮学院 电子科学与工程系，河南 驻马店 463000）

传统的CV模型只能用于分割灰度分布比较均匀、目标与背景灰度均值差异较大的图像，且因需要求解偏微分方程导致分割速度很慢．文章在传统快速水平集分割模型的基础上，将高斯分布估计引入速度项，使得快速水平集可以分割复杂的目标，并将 HIS空间中的色调分量与强度分量进行融合，得到了一种彩色高斯快速模型．新算法具有分割速度快、可分割复杂目标的优点．

CV模型；快速水平集；高斯分布估计；彩色模型

0 引言

基于水平集的图像分割方法具有数值求解稳定性高、抗噪性能好、分割边界光滑连续等优点．由Chan和Vese提出的CV模型[1]是水平集分割方法中的经典模型，因其具有模型简单、抗噪性好等优点而得到了广泛应用．但是，CV模型存在两个缺陷：一是只能分割简单的目标，对于目标和背景灰度均值相近或者灰度分布不均匀的图像，分割效果不理想；二是分割速度慢，大大降低了其实用性．

为了分割较为复杂的目标，文献[2―3]提出了基于概率分布估计的水平集方法，文献[4]提出了局部的基于区域的水平集模型．这些模型在分割效果上有很大提高，但分割速度变得更慢．CV模型分割耗时是由偏微分方程和符号距离函数的求解过程决定的．为了提高分割速度，文献[5]提出了一种快速的符号距离生成方法，文献[6]提出了用源点映射扫描法加快符号距离函数计算的方法，文献[7]提出了通过引入符号函数惩罚项而避开符号距离函数求解的方法．但是，这些模型仍需求解偏微分方程，分割速度仍然不快．Shi等人在文献[8]中提出了一种无需求解偏微分方程的快速水平集方法，通过引入基于梯度和基于阈值的速度项，极大地提高了分割速度，但难以分割复杂目标．

本文将高斯分布估计思想引入快速水平集模型，通过改进速度项，得到一种新的基于高斯分布估计的快速水平集分割方法，并将HIS空间中的色调分量与强度分量进行融合，建立起一种彩色高斯分布估计模型．

1 传统CV模型及其存在的问题

基于水平集的活动轮廓模型分割方法又称几何活动轮廓模型．活动轮廓模型分割的基本思想是用能量泛函来表示曲线的某一状态，通过设计合适的能量泛函，当能量值最小时对应的曲线即是目标轮廓线．早期，演化曲线是用参数方程描述的，这种方法下，曲线的拓扑结构难以改变，灵活性差．水平集理论[9]提出后，曲线由原来的参数方程描述变为零水平集表示．水平集表示下，能量泛函求最值变为求解偏微分方程，使得数值求解的稳定性更好．

CV模型是基于水平集的活动轮廓模型分割法中的经典模型，其能量泛函为

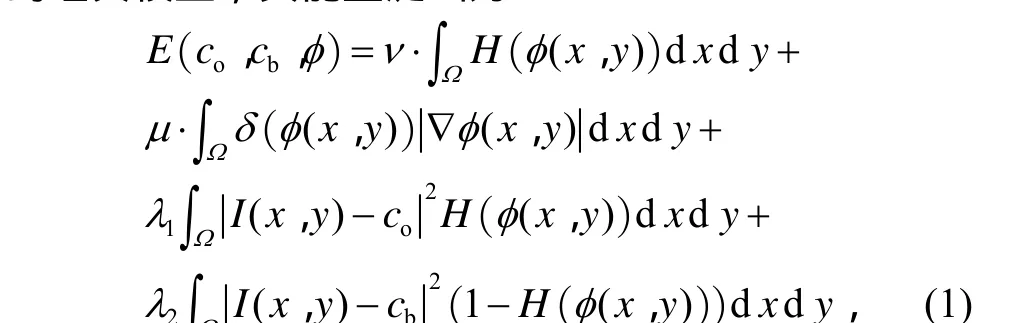
每次迭代都需要对(2)式进行一次运算，而(2)式中的每个变量都是和图像同样大小的矩阵，因此运算量很大．由公式(1)可以看出，当轮廓线内部和外部区域的灰度方差之和最小时，能量函数值最小，因此轮廓线内外区域的平均灰度差是曲线演化的驱动力，当目标和背景区域的平均灰度值相近时，演化曲线难以逼近正确的边界线．图 1(a)所示的是一幅人工图，原图大小为159像素×156像素，目标和背景区域的灰度均值相同但方差不同，利用传统CV模型分割的结果如图1(b)（分割失败），分割耗时8 s．图1(c)所示的豹子图像，目标较为复杂，原图大小为494像素×217像素，用传统CV模型分割的结果如图1(d)（分割失败），分割耗时32.58 s．图1(e)所示的斑马图像，原图大小为586像素×391像素，用传统CV模型分割的结果如图1(f)（分割失败），分割耗时45.34 s．可见，传统CV模型的分割速度慢，且难以分割复杂的目标．

图1 传统CV模型分割示例

2 基于高斯分布估计的快速水平集分割模型

文献[8]提出的快速实时水平集分割法，极大地提高了分割速度．

传统的水平集模型中，水平集函数用符号距离函数来表示．在快速水平集中，水平集函数被离散化为4个整数值，即

其中：水平集函数值小于0的区域是目标区域，记为Ωin，水平集函数值大于0的区域是背景，记为Ωout；水平集值为−3的区域称为内部区域（interior region），水平集值为+3的区域称为外部区域（exterior region）；水平集函数值为−1和+1的点分别属于内部链表和外部链表，其定义为

其中N(x)为点x的上下左右四邻域点．从上述定义可以看出，内部链表点是目标区域中与背景区域相邻的点，外部链表点是背景区域中与目标区域相邻的点．因此，可以用内部链表或外部链表来表示边界轮廓线．

快速水平集中的曲线演化通过交换内部链表和外部链表中的点来实现．如图2所示，曲线在点A处向外扩张，可以把A点从链表Lout中交换到链表Lin中；曲线在点B处收缩，可以把B点由链表Lin中交换到链表Lout中．元素的交换由switch_in和switch_out两种操作完成，switch_in操作将链表Lout中的点x交换到链表Lin中，实现曲线的扩张；switch_out操作将链表Lin中的点x交换到链表Lout中，实现曲线的收缩．这两种操作的执行规则是：对于Lout中的点，当该点的速度项大于0时，执行switch_in操作，否则不执行；对于Lin中的点，当该点的速度项小于 0时，执行switch_out操作，否则不执行．可见，速度项决定着曲线以何种方式演化．文献[8]中给出了两个速度项，一个是基于梯度的，另一个是基于区间阈值的，模型简单，但难以分割复杂的对象．

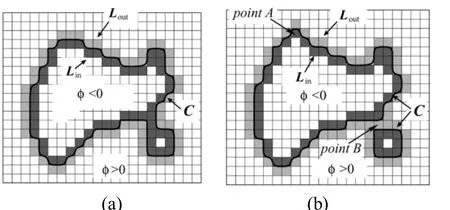
图2 快速水平集曲线演化示意图

为了使快速水平集可以分割复杂的目标，本研究将高斯分布估计引入速度项，得到一种新的速度项．为解决色彩信息丰富的复杂图像分割问题，本研究将HIS空间中的色调分量和强度分量进行融合，得到一种彩色高斯快速模型．

基于高斯分布估计的快速速度项公式为

其中I(x，y)是点(x，y)处的灰度值，uin和uout分别是轮廓线内部区域和外部区域的平均灰度值，σin和σout分别是轮廓线内部区域和外部区域的灰度方差．每次迭代后，都需要对内、外区域的均值和方差进行更新，均值和方差公式分别为

其中H（）φ为水平集函数．

为分割色彩信息丰富的图像，这里提出一种彩色高斯分布估计速度项，其公式为

其中λI和λH是加权系数，FH是对HIS空间的色调分量进行高斯估计，计算公式为

基于高斯估计的快速水平集分割算法的具体流程如下：

(1) 设定初始化轮廓线，初始化水平集函数、Lin链表和Lout链表．

(2) 更新轮廓线内部和外部区域的平均灰度值及方差（如果是彩色模型需要同时计算平均色调及方差）．先遍历链表Lout中的点，计算当前点的速度项F，若F＞0则执行switch_in操作；再次遍历链表Lout并删除不再属于该链表的点．同样，遍历链表Lin中的点，计算当前点的速度项F，若F＜0则执行switch_out操作；再次遍历链表Lin并删除不再属于该链表的点．

(3) 重复执行第 2步直至满足迭代终止条件．迭代终止条件有两种：一种是人工设定迭代次数；另种是链表Lout中任意点的速度项F＜0且链表Lin中任意点的速度项F＞0．

3 实验结果

图3显示了利用本文提出的基于高斯分布估计的快速水平集算法的分割结果，其中：图3(a)、图3(b)显示的分别是图1(a)所示人工图的初始化曲线和分割结果，目标区域基本上被分割开；图3(c)显示的是一幅X射线图的初始化曲线，具有灰度分布不均匀，部分边缘模糊的特点，其分割结果如图3(d)所示，目标基本上被分割开；图3(e)、图3(f)显示的分别是豹子图像的初始化曲线和分割结果，豹子的轮廓被完整地分割开．

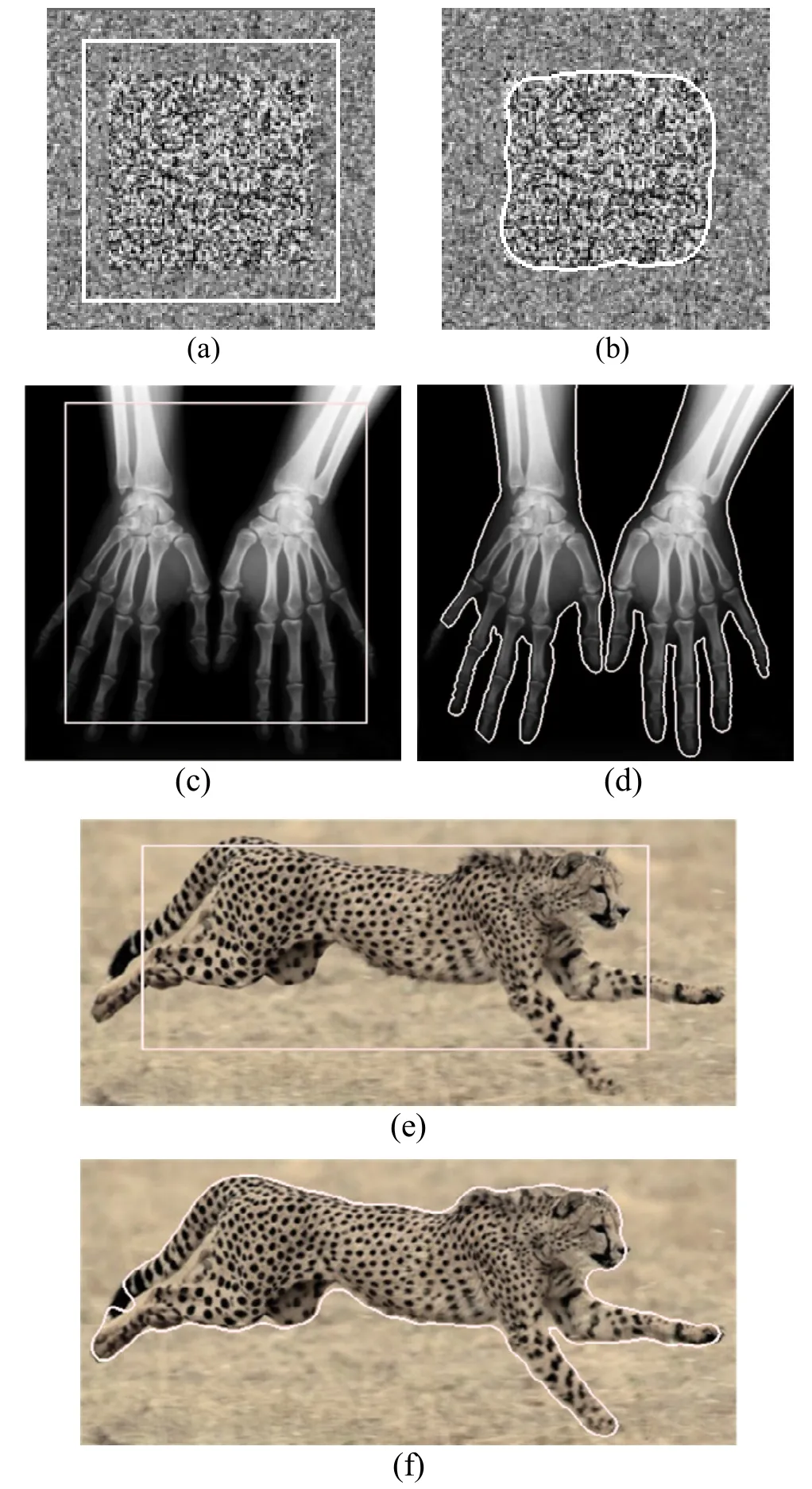
图3 高斯估计快速模型分割实验示例

图1(e)中的斑马图像色彩信息较为丰富，使用本文的彩色高斯快速模型进行分割实验，结果如图4所示，斑马轮廓被较好地分割出来．

图4 彩色高斯快速模型分割实验示例

表1给出了用传统方法和本文提出的改进方法分割上述图片的分割速度对比．可以看出本文提出的改进方法有效地提高了分割速度．

表1 传统水平集与本文改进算法分割时间对比

以上通过对传统CV模型及传统快速水平集的分析研究，针对其存在的问题，将高斯分布估计引入速度项，使得快速水平集可以分割复杂的目标，并将HIS空间中的色调分量与强度分量进行融合，得到了一种彩色高斯快速模型．实验结果表示，本文提出的新模型可以分割目标与背景灰度概率分布不同的图像，分割能力和分割速度与传统水平集方法相比都有很大的提高．

[1] Tony F Chan，Luminita A Vese．Active contours without edges[J]．IEEE Transactions on Image Processing，2001，10(2)：266―277．

[2] 杨鸿波，时永刚，邹谋炎．一种非参数估计的活动围道图像分割方法[J]．电子信息学报，2004(12)：1849―1855．

[3] 孙文杰，陈允杰，汤杨，等．一种改进的活动区域轮廓模型——无需水平集重新初始化[J]．计算机工程与应用，2008，44(2)：8―11．

[4] Li Chunming，Kao Chiu-Yen，Gore J C，et al．Minimization of Region-Scalable Fitting Energy for Image Segmentation[J]．IEEE Transactions on Image Processing，2008，17：1940―1949．

[5] 张博，苏永利．一种快速的符号距离函数的生成方法[J]．计算机应用软件，2008(6)：102―103．

[6] 李俊，杨新，施鹏飞．基于Mumford-Shah模型的快速水平集图像分割方法[J]．计算机学报，2002，25(11)：1177―1178．

[7] Li C，Xu C，Gui C，Fox M．Level set evolution without re-initialization: a new variational formulation[C]//Proceedingsof the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition，2005：1―7．

[8] Yonggang Shi，William Clem Karl．A Real-Time Algorithm for the approximate of Level-Set-Based Curve Evolution[J]．IEEE Transactions on Image Processing，2008，17(5)：645―656．

[9] Osher S，Sethian J A．Fronts propagating with curvaturedependent speed: algorithms based on Hamilton Jacobi formulations[J]．Journal of computational physics，1988，79：12―49．

Research on Fast Level Set Segmentation Method based on Gauss Distribution Estimation

ZHANG Si-wei
(Huanghuai University, Zhumadian Henan 463000, China)

The traditional CV model can only be used for the segmentation of the image whose gray distribution is uniform and whose targets and background have a big difference in gray level. The segmentation speed is very slow due to the need of solving partial differential equations during the segmentation process. On the base of the traditional fast level-set segmentation model,Gauss distribution estimation is introduced into a fast level-set method and a new fast level-set method segmentation algorithm is developed. The new algorithm has the advantages of fast segmentation speed and the segmentation of complex targets.

CV model; fast-level-set method; Gauss distribution estimation; color model

TP391

A

1006-5261(2012)02-0011-04

2012-02-17

张思维（1979―），男，河南项城人，讲师，硕士．

〔责任编辑 张继金〕