过等参测地线的B样条曲面重构

杨火根

(江西理工大学理学院，江西赣州341000)

过等参测地线的B样条曲面重构

杨火根

(江西理工大学理学院，江西赣州341000)

基于一般正则曲面上测地线的几何特征以及B样条乘积和升阶理论，构造了一类B样条曲面插值预先给定的B样条曲线,使这些曲线成为所构造曲面的边界等参测地线.该方法显式地计算了插值曲面上与插值条件相关的控制顶点，并且测地线插值条件中自由参数对曲面形状的影响具有局部性，插值曲面内部的自由控制顶点可作为曲面形状调整一种手段.与传统Coons超限插值方法不同，该方法所构造的插值曲面表示成标准的张量积B样条形式，与当今主流CAD系统的内在要求一致.计算实例表明该方法可行.

B样条曲面；B样条乘积；插值；测地线

0 引言

测地线，曲面上测地曲率处处为零的曲线，因其优美的内蕴几何性质，使得它在工业设计与加工等领域得到了广泛应用[1-3].例如在制鞋和成衣加工中，Wang等[4]对这一问题作了研究，他们以足背线和身腰线为测地线，给出了过这些公共测地线的非多项式形式曲面束的设计方法.然而当今主流CAD系统曲线曲面大多以多项式形式表示[5]，所以构造多项式形式的曲面成为后续研究主流.在非相交等参测地线插值曲面构造中，主要采用Hermite插值法[6-7]和二步法[8-10]等.而在相交测地线插值中，则一般采用Coons超限插值法[11-12].然而受测地线插值条件约束和构造方法所限，自由参数对曲面形状的影响往往带有整体性.并且曲面若以Bézier形式表示，其次数将达到13×13次[11].

目前，测地线插值中的曲线曲面主要还集中在一般多项式和Bézier形式上，而基于CAD系统中另一种曲线曲面表示形式(即B样条形式)的研究还未发现.文中考虑基于B样条方法的测地线插值问题，可利用B样条所特有的一些性质来解决上述测地线插值中的一些缺陷，如形状参数影响的整体性，相交测地线插值中曲线曲面次数过高问题等.由于测地线插值条件中包含测地线的一阶和二阶导矢向量积，为满足某些高品质曲面C2连续需要(如汽车行业、消费类产品中的A级曲面)，文中假定测地线为5次C4连续B样条曲线.

1 预备知识

为显式表示插值曲面控制顶点，首先简要介绍B样条乘积和升阶理论（具体细节可参考文献[13]）.设两B样条函数系数，Nj1，k1（t）和Nj2，k2（t）分别为定义在节点向量Γ1,Γ2上的k1和k2次B样条基函数.记k=k1+k2，节点向量Γ={…，ti，ti+1，…，ti+k，ti+k+1，…}，且节点ti∈Γ1或ti∈Γ2，其重数m满足：

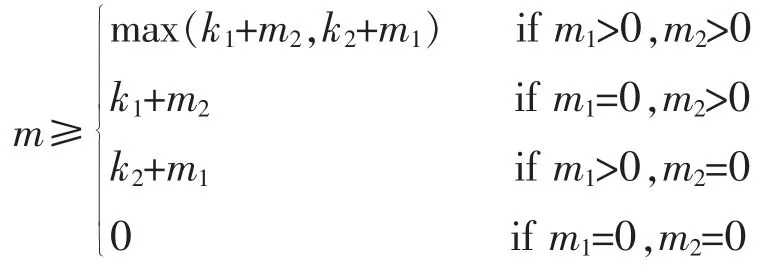
其中m1和m2为节点ti在Γ1,Γ2中的重数.集合Ik={1，2，…，k}，从Ik中任取k1个数组成集合p={p1，…，pk1}，剩下的k2个数组成集合Q={q1，…，qk2}，对给定的i，记节点向量ΓP={…，ti，ti+p1，…，ti+pk1，ti+k+1，…}，ΓQ={…，ti，ti+q1，…，ti+qk2，ti+k+1，…}，则有:

引理1[13]f1,f2，k及节点向量Γ1,Γ2,ΓP,ΓQ,Γ如上所述，则两B样条函数的乘积f1（t）f2（t）能被定义在节点向量Γ上的k次B样条基函数表示，即

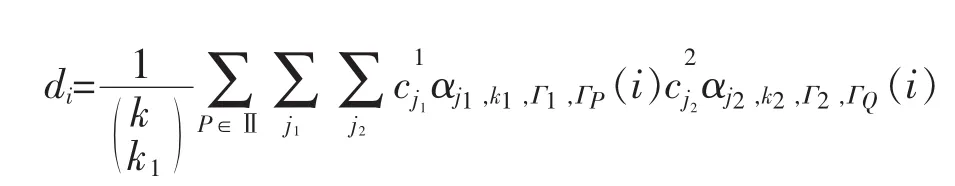
其中αj1，k1，Γ1，ΓP和αj2，k2，Γ2，ΓQ为离散B样条，Ⅱ表示P的所有可能性选择.

引理2[13]定义在节点向量Т1上的k1次B样条被表示成定义在节点向量Т上的k（k〉k1）次B样条函数

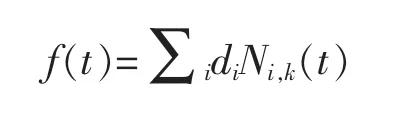
对任一空间曲线r（t），满足r′（t）×r″（t）≠0，记曲线在任一点t处的单位切向量、主法向量和副法向量为e（t），n（t）和b（t），其这三个向量两两正交，构成曲线在点r（t）处的Frenet局部坐标架.

2 B样条曲面插值测地边界线

假设两条给定的5次B样条曲线如下：

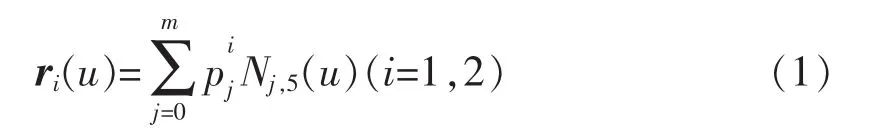
不妨设曲面R（u，v）以ri（u）为u向边界测地线，则ri（u）上任意点处的主法向量平行于曲面R（u，v）在该点的法向量，因此曲面在该点的切平面可由向，从而插值曲面在边界线ri（u）上的跨界切矢Rv（u，vi）可表示为：

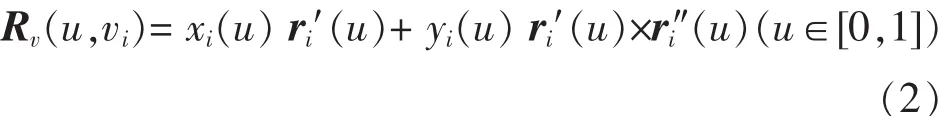
其中，当i=1时，vi=0；当i=2时，vi=1.由于′（u）×（u）为6次(因′（u）与ri″（u）的最高次系数向量平行)，考虑到曲面R（u，v）至少达到C2连续并且次数尽量较低，这里取yi（u）为非零常数bi，xi（u）为二次B样条函数义在节点向量T0={0,0,0,1,1,1}上.

下面将式（2）表示成B样条形式.记

和Nj2，3（u）分别定义在节点向量T′和T″上，且T″′，T″与节点向量U有相同的内节点.

根据引理1，fi（u）可以表示成如下6次B样条曲线：

同理，利用矢量积的坐标表达式和引理1，gi（u）可以表示为7次C2连续的B样条曲线，不妨记其控制顶点为（j=0，1，…，5m-18），节点向量为，其中的相异内节点值与U的内节点值相同，但重数为5.由于q次多项式曲线r（u）的矢量积r′（u）×r″（u）为2q-4次多项式曲线（因为r′（u）和r″（u）最高次项的向量系数平行），ri（u）为分段5次多项式曲线，因此在节点向量的每个非零子区间上gi（u）实际次数为6，即gi（u）实际上为定义在节点向量T上的6次C2连续B样条曲线，设其表达式为：

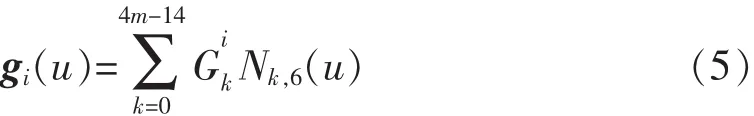
由式（3）、式（4）、式（5）可得Rv（u，vi）的B样条表示为：

为确定插值曲面相关控制顶点，再将两条测地边界线表示成式(6)的形式，由引理2有：

因插值曲面v向边界线无约束，不妨设为3次B样条曲线，其节点向量为V={v0，…，v3，v4，…，un，un+1，…，un+4}，uk＜vk+1（k=3，…，n），v0=…=v3=0，un+1=…=un+4=1记：

由式

对R（u，v）关于v求偏导，分别令v=0和1，联合式（6）、式（8）得：

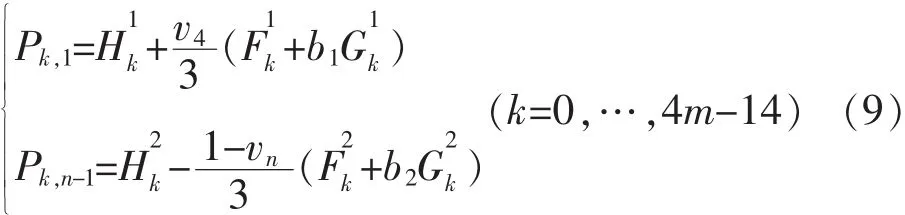
从式（9）可知，测地线插值条件（2）仅与曲面边界线的控制顶点及邻接边界线的控制顶点有关，其他控制顶点是自由的.也就是说，若曲面R（u，v）以ri（u）为u向边界线，当其两条u向边界线的控制顶点由式（8）决定，邻接边界线的那两排控制顶点由式（9）确定，其他内部控制顶点自由选择，则曲面R（u，v）必以ri（u）为u向边界测地线.

按上述方法，基于OpenGL用C语言编程,6×3次C2连续B样条曲面R（u，v）插值两条给定的空间B样条曲线为曲面等参边界测地线的实例见图1.图1（a）表示由式(1)定义的两条B样条曲线（m=7）及其控制多边形，图1（b）表示由式（8）、式（9）确定的插值曲面两条边界线的30个控制顶点（红色）、邻接边界线的30个控制顶点（蓝色）及其控制多边形.

图1 B样条曲面插值等参测地线

3 结论

文中给出了构造一类B样条曲面插值给定曲线为曲面边界测地线的方法，当给定的边界线为5次C4连续B样条曲线时，插值曲面显式地表示为6×3次C2连续的张量积B样条曲面.与插值条件相关的曲面控制顶点的显式表示说明测地线插值仅与曲面边界线和邻接边界线的那排控制顶点有关，与曲面内部其他控制顶点无关，这使得插值条件中的自由参数仅影响曲面的局部形状，其他区域形状可通过内部自由的控制顶点来调整.插值曲面表示为标准的张量积B样条形式，符合当今CAD系统的表示要求.该方法可推广到相交测地线的插值曲面构造，以解决目前插值曲面次数偏高等缺陷.

[1]杨庆山,姜忆南.张拉索-膜结构分析与设计[M].北京:科学出版社,2004.

[2]张连东，王德伦.一种基于测地线的机器人轨迹规划方法[J].机器人，2004,26(1):83-86.

[3]Tucker III C L.Forming of advanced composites:Advanced Composites Manufacturing[M].New York：Gutowski,1997:297-372.

[4]Wang Guojin,Tang Kai,Tai Chiew-lan.Parametric representation of a surface pencil with a common spatial geodesic[J].Computer-Aided Design,2004,36(5):447-459.

[5]杨火根，赖新兴.一类相邻NURBS曲面G1光滑拼接算法[J].江西理工大学学报,2006,27(4):41-44.

[6]Sprynski N,Szafran N,Lacolle B,et al.Surface reconstruction via geodesic interpolation[J].Computer Aided Design,2008,40（4）:480-492.

[7]赵宏艳,王国瑾.过测地线的优化曲面设计[J].计算机研究与发展,2009,46(2):289-294.

[8]Sanchez Reyes J,Dorado R.Constrained design of polynomial surfaces from geodesic curves[J].Computer-Aided Design，2008,40（1）:49-55.

[9]Paluszny M.Cubic polynomial patches through geodesics[J].Computer-Aided Design,2008,40（1）:56-61.

[10]Yang Huo-gen,Zou Wei-gang.Optimized design Bézier surfaces interpolation geodesics[C].T Proceedings of the T3rdT IEEET International Symposium on Information Science and Engineering，2010,12:550-553.

[11]Farouki R T,Szafran N,Biard L.Construction of Bézier surface patches with Bézier curves as geodesic boundaries[J].Computer-Aided Design,2009,41(11):772-781.

[12]Farouki RT,Szafran N,Biard L.Construction and smoothing of triangular Coons patches with geodesic boundary curves[J].Computer Aided Geometric Design,2010,27(4):301-312.

[13]Mφrken K.Some identities for products and degree raising of splines[J].Constructive Approximation,1991,7:195-208.

Reconstruction of B-spline surfaces through isoparametric geodesics

YANG Huo-gen
（Faculty of Science,Jiangxi University of Science and Technology,Ganzhou 341000,China）

Based on the geometric features of geodesic on regular surface and the theory of products and degree raising of B-spline,a B-spline surface interpolating the given space B-spline curves is constructed.The curves are isoparametric boundary geodesics of the constructed surface.The control points associating with interpolation conditions are computed explicitly.The free parameters of the geodesic interpolation conditions only affect the local shape of surface,and the shape of the interpolating surface can be adjusted by its free inner control points.Being different from the traditional Coons interpolation scheme,the constructed surface is presented as standard tensor-product B-spline form,which is compatible with modern CAD systems.The method is illustrated with computational examples.

B-spline surfaces;products of B-spline;interpolation;geodesic

O241.5

A

2012-07-05

江西省自然科学青年基金项目(2009GQS0047)；江西理工大学科研基金项目计划（jxxj11062）

杨火根(1975-)，男，副教授，主要从事CAGD和反向工程等方面的研究，E-mail:yanghuogen@126.com.

2095-3046（2012）05-0093-04