时间延迟在随机系统中的作用
刘圣君,王祺,丰海,1b
(1.厦门城市学院,a.电子通信教研室;b.嵌入式Linux应用中心,福建厦门361008;2.日本筑波大学化学系,日本筑波305-8571)
时间延迟在随机系统中的作用
刘圣君1a,王祺2,丰海1a,1b
(1.厦门城市学院,a.电子通信教研室;b.嵌入式Linux应用中心,福建厦门361008;2.日本筑波大学化学系,日本筑波305-8571)
文中通过一个具体的模型,阐明了时间延迟在一些动力学系统中的重要作用.当输出信号由自身调控的延迟时间为零时,只有低频部分的功率谱对延迟时间的变化敏感,这个延迟时间是由输入信号调控输出信号引起的.对于输入信号而言,随着延迟时间的增加,主峰的高度和峰的数目都是增加的.同时,对输出信号而言,随着延迟时间的增加,峰的数目是增加的,而主峰的高度则没有发生变化.然而,当输出信号被输入信号调控的延迟时间为零时,随着输出信号由自身调控的延迟时间的变化,输出信号比输入信号呈现出更为复杂的行为.
时间延迟;动力学;机理;振荡;功率谱
0 引言
研究随机系统的动力学机理的一个重要因素是时间延迟(Time delay),在许多实际的随机系统中时间延迟是不可避免的,它反映了与系统的物质,能量及信息输运相关的传递时间[1-5].Strogatz[1]为解释时间延迟的实质,曾经举过一个形象的例子:当用旧式的淋浴器时,一开始流出的水是冷的,于是调高水温,可是水并没有马上变热,这是由于旧式的加热器从开始加热到放出热水需要消耗一定的时间.可是这时如果再继续调高水温则会带来麻烦,水温超过了人们最初的需要,可能会变得很烫,这时也只能再调低水温.如此地反复调节,就引起了水温的一系列振荡行为.实验研究表明[2,5],在很多实际的生物系统中,当某个生化反应所消耗的时间要明显多于系统中其它反应所需要的时间时,时间延迟所起的作用就相当重要.因而,研究者们在研究随机系统的网络单元时,经常会在模型中引入一个时间延迟[5-8],或者多个时间延迟[9-14].引入延迟的基本思想是把涉及到大分子序列的复杂的多步过程简化为一个单一的带延迟的过程[15].基本的方法是消除复杂的多步过程中的快反应,并且用一个特征延迟时间来保留慢反应.延迟效应的引入对在分子水平上研究随机动力学,以及理解发生在所有网络模块中的整个动力学都有着十分重要的意义[3-6,16].
Monk等的结果表明,时间延迟的引入,不仅使得复杂的生化反应动力学得到简化,更重要的结论是时间延迟是引起基因调控网络中振荡现象的重要原因[5].2003年被提出的Lewis模型[6]和Monk模型[5]就是典型的例子,至今还在不断地被进行深入研究[12,17-20].时间延迟引起的这种振荡现象不仅在生物系统,在整个自然界内都普遍地存在着.因此,时间延迟的引入不仅是描写生化反应本身的内在需要,也是为了能更好地解释这些振荡系统内普遍存在的物理机制.理论研究表明,时间延迟能为系统带来非线性效应,时间延迟的大小是影响系统动力学特性的重要因素[11-21],同时也是影响系统稳定性的重要因素[13-14,16].近年来,对于时间延迟系统模型的研究广泛地深入到基因调控网络[5-6]、生理节奏振荡[22-23]、免疫系统[14]、细胞周期[8]、神经网络[24-25]及生态系统[26]等方面.文献[4]列出了一些延迟系统的例子,并给出了相应的特征延迟时间.
文中通过一个具体系统的模型,引入了时间延迟,并通过数值计算其功率谱,进一步阐明了时间延迟在动力学系统中的重要作用,数值计算的结果表明,时间延迟是引起动力学系统振荡现象的重要原因.时间延迟的引入,会引起功率谱的主峰高度以及峰的数目的增加,因而,反应出系统振荡强度的增加.本工作将对研究实际随机系统的振荡具有重要的指导意义.例如,生理节奏振荡的周期和细胞周期都能通过功率谱的分析获得.通过计算功率谱的最低峰的频率,能预测随机系统的振荡周期.并对在分子水平上研究随机系统的动力学,以及理解发生在所有网络模块中的整个动力学都有着潜在的意义.
1 模型和分析
下面通过一个具体的模型,来考查时间延迟在一些动力学系统中的重要作用.此模型是从最普遍的生物网络模块出发,这个模块也是相对比较简单的却有很大程度的生物相关性.在蛋白质的降解过程中,时间延迟作为一个很重要的关键点被考虑,同时,也考虑了源于内噪声和外噪声的随机行为.文中的模型由以下一组典型的郎之万方程表示:

其中X代表输出信号,S代表输入信号.这方面的动力学实例可以参见文献[27].τ1是输出信号X被输入信号S调控的延迟时间,τ2是输出信号X由自身调控的延迟时间.A和C分别是带延迟的信号合成和消失的速率.B是不带延迟的信号消失的速率.k1和k-1代表随机系统从一种状态变化到另外一种状态的速率.文中考虑的是随机系统,此系统的内噪声用η1(t)表示,外噪声用η2(t)表示,它们都是如下形式的高斯白噪声:

用X(t)和S(t)对方程(1)和方程(2)做如下代换:

其中,X*和S*分别代表无延迟时确定性方程(1)和方程(2)的稳定解,表示如下:

其中,∈=k1/k-1代表网络的反馈强度,方程(1)和方程(2)可代换为:

其中,E=k-1+k1X*,F=k1S*.对方程组(6)和方程组(7)进行傅里叶变换可得:

接着用插值法求解方程组(8)和方程组(9),并且忽略高阶项.取弱噪声和弱反馈近似,x(ω)和s(ω)的解保留到η1(ω)和η2(ω)的二阶项,这种近似是合理的[28-29].定义如下中间变量[29]:
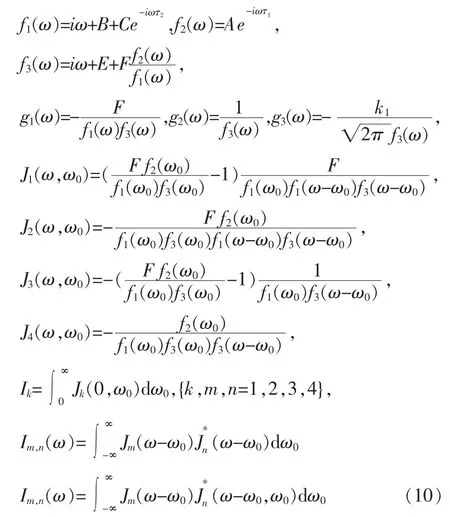
由方程组(8)和方程组(9)可以得到x(ω)和s(ω)功率谱:

其中,


图1 输入信号和输出信号的功率谱随延迟时间的变化

数值计算的结果见图1.
从图1可以看出和时间延迟效应相关的输入信号S和输出信号X的功率谱的振荡情况,其中的参数分别是A=1,B=2,C=1,k-1=1,∈=1.当τ2=1时,只有低频部分的功率谱对延迟时间τ1的变化敏感.对于输入信号S而言,随着τ1的增加,主峰的高度和峰的数目都是增加的.同时,对输出信号X而言,随着τ1的增加,峰的数目是增加的,而主峰的高度则没有发生变化.接下来考查当τ1=0时,τ2对输入信号S和输出信号X的功率谱的影响,输出信号X比输入信号S呈现出更为复杂的行为.在功率谱的低频部分,对s(t)和x(t)的谱Ss(ω)和Sx(ω)来说,随着τ2的增大,振荡的强度是增强的,且峰的数目也是增加的.
2 小结
时间延迟是研究随机系统动力学机理的一个重要因素,在许多实际的随机系统中时间延迟也是不可避免的.文中通过一个具体的模型,阐明了时间延迟在一些动力学系统中的重要作用.通过推导模型中输入信号S和输出信号X的功率谱并进行数值计算,可以得到和时间延迟效应相关的输入信号S和输出信号X的功率谱的一些重要的信息,当输出信号X由自身调控的延迟时间τ2=0时,只有低频部分的功率谱对输出信号X被输入信号S调控的延迟时间τ1的变化敏感.对于输入信号S而言,随着τ1的增加,主峰的高度和峰的数目都是增加的.同时,对输出信号X而言,随着τ1的增加,峰的数目是增加的,而主峰的高度则没有发生变化.然而,当输出信号X被输入信号S调控的延迟时间τ1=0时,随着输出信号X由自身调控的延迟时间τ2的变化,输出信号X比输入信号S呈现出更为复杂的行为.在功率谱的低频部分,对s(t)和x(t)的谱Ss(ω)和Sx(ω)来说,随着τ2的增大,振荡的强度是增强的,且峰的数目也是增加的.
本研究方法对研究实际的随机系统具有重要的理论和实际意义,例如,生理节奏振荡的周期和细胞周期都能通过功率谱的分析获得.通过数值计算功率谱的最低峰的频率,能预测随机系统的振荡周期.进而,还能预测随机系统的演化方向.并对在分子水平上研究随机系统的动力学,以及理解发生在所有网络模块中的整个动力学都有着潜在的意义.
[1]Strogatz S H.Death by delay[J].Nature,1998,394:316-317.
[2]Hirata H,Yoshiura S,Ohtsuka T,et al.Oscillatory expression of the bHLH factor Hes1 regulated by a negative feedback loop[J].Science,2002,298(5594):840-843.
[3]Lev Bar-Or R,Maya R,Segel L A,et al.Generation of oscillations by the p53-Mdm2 feedback loop:A theoretical and experimentalstudy[J].Proc.Natl.Acad.Sci.USA,2000,97(21):11250-11255.
[4]Frank T D,Beek P J,Friedrich R.Fokker-Planck perspective on stochastic delay systems:Exact solutions and data analysis of biological systems[J].Phys.Rev.E,2003,68(2):21912-21921.
[5]Monk N A M.Oscillatory expression of Hes1,p53,and NF-kB driven by transcriptional time delays[J].Current Biology,2003,13(16):1409-1413.
[6]Lewis J.Autoinhibition with transcriptional delay:A simple mechanism for the zebrafish somitogenesis oscillator[J].Current Biology,2003,13(16):1398-1408.
[7]Srividhya J,Gopinathan M S,Schnell S.The effects of time delays in a phosphorylation-dephosphorylation pathway[J].Biophysical Chemistry,2007,125(2-3):286-297.
[8]Albeck J G,Burke J M,Spencer S L,et al.Modeling a snapaction,variable-delay switch controlling extrinsic cell death[J].PLOS Biology,2008,6(12):2831-2852.
[9]Srividhya J,Gopinathan M S.A simple time delay model for eukaryotic cell cycle[J].Journal of Theoretical Biology,2006,241(3):617-627.
[10]Adimy M,Crauste F,Ruan S G.Periodic oscillations in leukopoiesis models with two delays[J].Journal of Theoretical Biology,2006,242(2):288-299.
[11]Song Y L,Peng Y H,Wei J J.Bifurcations for a predator-prey system with two delays[J].Journal of Mathematical Analysis and Applications,2008,337(1):466-479.
[12]Wu H X,Liao X F,Guo S T,et al.Stochastic stability for uncertain genetic regulatory networks with interval time-varying delays[J].Neurocomputing,2009,72(13-15):3263-3276.
[13]Tanaka Aki S M,Sandra M.S.de Godoy.Permanence of stability for a class of system of differential equations with two delays[J].NonlinearAnalysis:RealWorldApplications,2009,10(1):172-184.
[14]Yu C B,Wei J J.Stability and bifurcation analysis in a basic model of the immune response with delays[J].Chaos,Solitions&Fractals,2009,41(3):1223-1234.
[15]Zhu R,Salahub D.Delay stochastic simulation of single-gene expression reveals a detailed relationship between protein noise and mean abundance[J].FEBS Letters,2008,582(19):2905-2910.
[16]Yan S W.Negative feedback dynamics and oscillatory activitiesin regulatory biological networks[J].Journal of Biological Systems,2007,15(2):123-138.
[17]Veflingstad S R,Plahte E,Monk N A M.Effect of time delay on patternformation:Competitionbetweenhomogenisationand patterning[J].Physica D:Nonlinear Phenomena,2005,207(3-4):254-271.
[18]Rateitschak K,Wolkenhauer O.Intracellular delay limits cyclic changes in gene expression[J].Mathematical Biosciences,2007,205(2):163-179.
[19]Novak B,Tyson J J.Design principles of biochemical oscillators[J].Nat.Rev.Molecular Cell Biology,2008,9(12):981-991.
[20]Ribeiro A S.Stochastic and delayed stochastic models of gene expression and regulation[J].Mathematical Biosciences,2010,223(1):1-11.
[21]Yan S W,Zhuo Y Z.A unified model for studying DNA damageinduced p53-Mdm2 interaction[J].Physica D:Nonlinear Phenomena,2006,220(2):157-162.
[22]Sriram K,Gopinathan M S.A two variable delay model for the circadian rhythm of Neurospora crassa[J].Journal of Theoretical Biology,2004,231(1):23-38.
[23]Bohn A,Lopes J R,Diambra L A,et al.Delay model of circadian gene expression with two negative feedback loops[J].Biological Rhythm Research,2006,37(5):405-417.
[24]Monteiro L H A,Pellizari A,Chaui-Berlinck J G,et al.Oscillation death in a two-neuron network with delay in a selfconnection[J].Journal of Biological Systems,2007,15(1):49-61.
[25]Momiji H,Monk N A M.Oscillatory Notch-pathway activity in a delay model of neuronal differentiation[J].Phys.Rev.E,2009,80(2):21930.
[26]Nie L R,Mei D C.Effects of time delay on symmetric twospecies competition subject to noise[J].Phys.Rev.E,2008,7(3):31107.
[27]Bratsun D,Volfson D,Tsimring L S,et al.Delay-induced stochastic oscillations in gene regulation[J].Proc.Natl.Acad.Sci.USA,2005,102(41):14593-14598.
[28]Liu S J,Wang Q,Liu B,et al.Noise transmission and delayinduced stochastic oscillations in biochemical network motifs[J].Chinese Physics B,2011,20(12):128703.
[29]刘圣君.生物化学过程的随机动力学与统计性质研究[D].北京:北京师范大学,2010.
The effects of the time delay in the stochastic systems
LIU Sheng-jun1a,WANG Qi2,FENG Hai1a,1b
(1.Xiamen City University,a.Department of Electronic Communications;b.Embedded LINUX Application Center,Xiamen 361008,China;2.Department of Chemistry,Tsukuba University,Tennodai,Tsukuba 305-8571,Japan)
A prototype model is proposed and the important roles of the time delay in the dynamical systems are clarified in this paper.When the time delay regulated by the output signal is zero,only the power spectrum in the low frequency is sensitive to the change of time delay regulated by the input signal.To the input signal,the height and the number of the main peak increase with the increase of the time delay.While to the output signal,the number of the peak increases but there is no change in the height of the main peak.However,when the time delay of the output signal regulated by the input signal is zero,the output signal shows more complex action than the input signal with the change of the time delay of the output signal regulated by itself.
time delay;dynamics;mechanism;oscillation;power spectrum
O231.3
A
2012-09-06
2012年福建省高校杰出青年科研人才计划;2011年厦门城市职业学院重点课题(KY11-08)
刘圣君(1981-),女,博士,讲师,主要从事非线性动力学与统计理论、光伏电子等方面的研究,E-mail:liushengjunok@163.com.
丰海(1976-),男,博士,副教授,主要从事嵌入式系统等方面的研究,E-mail:fenghai@xmcu.cn.
2095-3046(2012)05-0056-04

