Arzela-Ascoli定理条件的改变和减弱

张亚林

（天津大学 理学院，天津 300072）

Arzela-Ascoli定理条件的改变和减弱

张亚林

（天津大学 理学院，天津 300072）

文章将Arzela-Ascoli定理中的闭区间［α，β］上的连续函数族扩展到无穷紧空间上的连续算子族，给出了无穷紧空间上的连续算子族相对紧性判断的一个充要条件；然后将定理中一致有界减弱为在一点有界，定理的结论仍然成立.

Arzela-Ascoli定理；相对紧；等度连续；一致有界

0 引言

Ascol-Arzelai定理对出了有限闭区间上连续函数族相对紧性判定的一个充要条件，其应用非常广泛，但局限于有限区间.对于这一结果，已经有很多推广，在文［1］中将闭区间［α，β］推广到紧空间K，指出C（K）的子集F是相对紧的当且仅当F等度连续且一致有界；文［2］也对Ascoli-Arzela定理进行了一定程度上的推广.但是这些推广都是在实值范围内进行的，本文将实值连续函数推广到向量值连续算子，即假设E为紧度量空间，X为Banach空间，C（E，X）表示从E到X的连续函数的全体，给出了C（E，X）上任一子集相对紧的充要条件，大大扩展了应用范围.另外，定理中的一致有界条件很强，如果能减弱为在一点有界的话，定理的适用范围将进一步扩大.

1 预备知识

定义1［3］设（X，ρ）是距离空间，A是X的子集，如果A中的任何点列必有在X中的收敛子列，则称A为紧集.

定义2［3］设（X，ρ）是距离空间，A是X的一个子集，B⊆A，如果有ε＞0，使得以B中各点为中心，以ε为半径的开球全体覆盖A，即A⊆U x∈BO（x，ε），则称B是A的ε网.如果B是有限集，则称B是A的有限ε网.

定义3［3］设（X，ρ）是距离空间，A是B的子集，如果对于任意ε＞0，都存在着A的一个有限ε网，则称集合A是完全有界的.

从下述引理可以看出，集合的相对紧性与完全有界有着重要的联系.

引理1［3］1）度量空间中相对紧集必是完全有界集；2）在完备度量空间中，完全有界集必是相对紧集.

引理2［3］设A是R n的子集，则A是相对紧的当且仅当A是有界的.

关于连续函数，有下面重要概念.

定义4［2，3］设F是C［α，β］的子集，

1）如果存在M＞0，使得对任意x∈［α，β］，任意f∈F都有｜f（x）｜≤M，则称F是一致有界的；

2）如果对于任意的ε＞0，存在δ＞0，使得对于任意两点x1，x2∈［α，β］，当｜x1－x2｜＜δ时，对F中每个函数f都有｜f（x1）－f（x2）｜＜ε，则称F是等度连续的.

引理3（Ascoli-Arzela）（［4］） 设F＝f（t）是定义在α≤t≤β上的一致有界且等度连续的实值（m维）向量函数族，则从F中必可选取一个在α≤t≤β上一致收敛的函数列｛f n（t）｝，（n＝1，2，…）.

2 主要结果

下面给出C（E，X）中的一些定义.

设E为紧空间，X是Banach空间，用C（E，X）表示E到X的连续函数全体，令

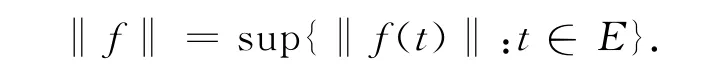
容易验证C（E，X）为Banach空间.对于C（E，X）的子集，也有类似的一致有界和等度连续的概念.

定义5［5］设F是C（E，X）的子集.

1）如果存在M＞0，使得对于任意x∈E，f∈F都有‖f（x）‖≤M，则称F是一致有界的；

2）如果对任意的ε＞0，存在δ＞0，使得对于F中的每个函数f都有‖f（x1）－f（x2）‖＜ε，则称F是等度连续的.

定义6［5］设f是从距离空间（X，ρ1）到距离空间（Y，ρ2）的一个映射，如果对任意ε＞0，存在δ＞0，使得对任意x1，x2∈X，当ρ1（x1，x2）＜δ时，有ρ2（f（x1），f（x2））＜ε，则称f是一致连续的.

注意到定义在闭区间上的实值函数如果连续，则必一致连续，下述引理显示这一结论对从紧距离空间到距离空间的连续算子也成立.

引理4 若f是从紧距离空间E到距离空间X的连续算子，则f是一致连续的.

定理1 若F⊆C（E，X）是相对紧的，则F是一致有界且等度连续的.

对于一般的Banach空间，C（E，X）中子集的相对紧性有如下定理.

定理2 令E为紧度量空间，X为Banach空间，F为连续映射族C（E，X）的子集，则F为相对紧的当且仅当下面两个条件满足：

1）F是等度连续的；

2）对于任意的x∈E，集合F（x）＝f（x）：f∈F是相对紧的.

证明 假设F满足两个条件.我们证明F是相对紧的，由已知X为Banach空间，故C（E，X）为完备的，由引理1，只需证明F为完全有界集.

因为F为同等连续的，即对任意的ε＜0，存在δ＝δ（ε）＞0，对于任意的f∈F，任意的x1，x2∈E，当ρ（x1，x2）＜δ时，

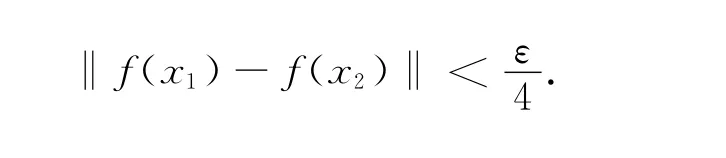
又E是紧度量空间，由引理1，对于上述δ＞0，存在｛x1，x2，…，x n｝⊂E，对于任意x∈E，存在1≤i0≤n，使得ρ（x，x i0）＜δ.

由条件2），F（x1），F（x2），…，F（x n）是相对紧的，故

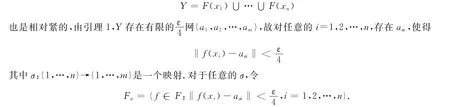
则有限个Fσ覆盖F，要说明Fσ为F的有限ε网，只需说明Fσ的半径为＜ε即可.对于任意的f，g∈Fσ，x∈E，

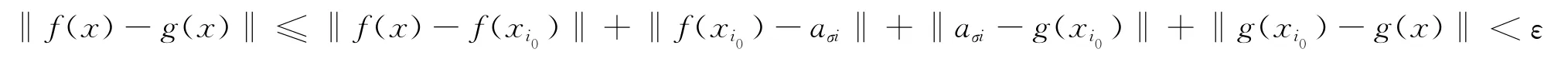
充分性得证.

下证必要性.对于等度连续，证法同定理1，对于2）由F的相对紧性易得.

现在我们将原定理中的条件适当减弱.

定理3 Ascoli-Arzela定理中函数族的一致有界性减弱为在某一点有界，结论依然成立.

证明 不妨设F在α点有界，我们只需证F一致有界.

由F等度连续，则对任意的ε＞0，存在δ＝δ（ε）＞0，对任意的f∈F，任意的x1，x2∈［α，β］，当｜x1－x2｜＜δ时，

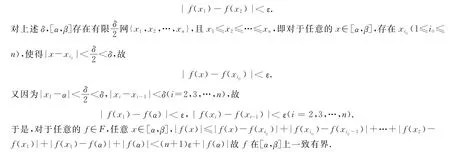
显然在这种较弱的条件下，定理的使用范围大大增大了.

［1］张恭庆，林源渠.泛函分析讲义［M］.北京：北京大学出版社，2004

［2］郭 伟.Ascoli-Arzela定理的一个推广及应用［J］.系统科学与数学，2002，22（1）：115-122

［3］夏道行，吴卓人，严绍宗.实变函数与泛函分析［M］.北京：北京大学出版社，1985

［4］尤秉礼.常微分方程补充教程［M］.北京：人民教育出版社，1981

［5］Serge L.Real and functional analysis［M］.Berlin：Spring Verlag，1993

A Change and Reduction of the Condition on Arzela′s Theorem

Zhang Yalin
（Institute of Science，Tianjin University，Tianjin 300072，China）

The continuous function groups in Arzela-Ascoli theoren which defined on［α，β］are reduced to a class of continuous operator groups defined on infinity dimension complact spaces，and the sufficient and necessary conditions are given for relative compactncss of a class of continuous operator groups.The uniformly boundedness condition is weakcned to bound in a point，the theorem is still on in this case.

Arzela-Ascoli theorm；relative compact；equicontinuous；uniformly boundedness

王映苗】

1672-2027（2012）01-0072-03

O174.1

A

2011-12-25

张亚林（1987-），女，山东河泽人，天津大学在读硕士研究生，主要从事方程谱理论的研究.