权重信息不完全的梯形模糊数多属性决策

张伟竞 黄天民 陈尚云

（西南交通大学 数学学院，四川 成都 610031）

权重信息不完全的梯形模糊数多属性决策

张伟竞 黄天民 陈尚云

（西南交通大学 数学学院，四川 成都 610031）

针对权重信息不完全且属性值为梯形模糊数的模糊多属性决策问题，给出了基于梯形模糊数质心的多属性决策方法，并通过投影法建立了非线性规划模型，通过数学软件得到各属性权重，并通过质心横坐标与纵坐标在虚拟理想方案上的投影率的乘积作为排序指标，进行排序择优.最后通过实例说明了该方法的有效性.

梯形模糊数；质心；投影率；多属性决策

0 引言

在很多多属性决策中，由于备选方案的模糊性和复杂性，决策者往往不能准确地给出决策方案的评价信息，而通常以模糊数的形式给出.因此，对各备选方案的排序和择优就成为重要的研究课题之一.

针对部分属性权重信息已知且属性值为梯形模糊数的多属性决策问题，根据质心横坐标与纵坐标重要程度的不同，给出了基于质心横坐标在虚拟理想方案上的投影法，建立了非线性规划模型，从而得到各属性权重向量，并进行择优.该方法便于用数学软件操作实现且较为简单，且提供了新的途径.

1 基本概念

2 决策理论与方法

3 决策实例

现考虑一个购买轿车的多属性决策问题，有4辆轿车分别为A1，A2，A3，A4，有3个属性G1，G2，G3分别为轿车价格，安全系数，总体设计，其中G1为成本型属性指标，G2，G3为效益型属性指标，属性集Gj（j＝1，2，3）的权重不能完全确定.已知的部分权重信息为：w3－w2≤0.2，w1－w3≤0.35，0.6w1≤wi≤0.8w1.决策矩阵A为：

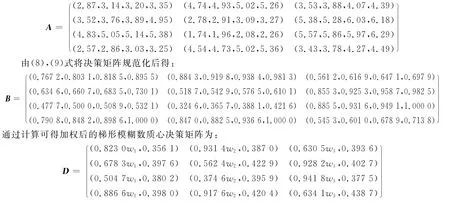
4 结束语

针对上述多属性决策问题，依据质心横坐标和纵坐标重要程度的不同，通过质心核横（纵）坐标来建立规划模型，并进行决策，该方法便于在计算机上操作实现，并且梯形模糊数的质心更能体现加权后梯形模糊数的所有信息，最后通过决策实例，说明这类决策模型的有效性和实用性.

［1］ Wang Y M，Yang J B，Xu D L，et al.On the centroids of fuzzy number［J］.Fuzzy Sets and Systems，2006，157：919-926

［2］ Wang Y J，Lee S H.The revised method of ranking fuzzy numbers with an area between the centroid and original point［J］.Computer ＆ Mathematics with Applications，2008，55：2 033-2 042

［3］ 王应明.多指标决策与评价的新方法－投影法［J］.系统工程和电子技术，1999，21（3）：1-4

［4］ Lee K S，Park K S，Eum Y S.Extend methods for identifying dominance and potential optimality in multicriteria analysis with imprecise information［J］.European Journal of Operational Research，2001，134（4）：557-563

［5］ Kim S H，Han C H.An interactive procedure for multiple attribute group decision making procedure with incomplete information［J］.Computer ＆ Operational Research，1999，26（8）：755-772

［6］ 吴 超，胡 昆.区间数多属性决策中权重灵敏度分析［J］.系统工程和电子技术，2004，26（2）：1 217-1 219

［7］ 徐泽水.不确定多属性决策方法及应用［M］.北京：机械工业出版社，2001

［8］ 李荣均.模糊多准则决策理论与应用［M］.北京：科学出版社，2002

［9］ 卫贵武.基于模糊信息的多属性决策理论与方法［M］.北京：中国经济出版社，2010

Multiple Attribute Decision Making of Trapezoid Fuzzy Numbers Based on Attribute Weight Information is Incomplete

Zhang Weijing Huang Tianmin Chen Shangyun
（Department of Mathematic，Southwest Jiaotong University，Chengdu 610031，China）

With respect to multiple attribute decision making problems in which the attribute weight information is incomplete and the attribute values are trapezoid fuzzy numbers.Given a new method based on the centroid point of trapezoid fuzzy numbers，and how decisions by the projection method for nonlinear planning model，using software of mathematics for solve each attribute weight，and ranking with the product on the centroid point on horizontal axis and vertical axis the projection rate on the ideal solution，according to the relational degree，all alternatives are ranked.Finally，a numerical example is provided to illustrate the effectiveness of the method.

trapezoid fuzzy numbers；centroid point；the projection；multiple attribute decision making

王映苗】

1672-2027（2012）03-0053-04

C934；O29

A

2012-05-10

张伟竞（1986-），男，山西晋城人，西南交通大学在读硕士研究生，主要从事模糊优化与决策研究.