基于遗传算法的广义回归神经网络在地震预测中的应用

韩晓飞，潘存英，罗词建

（1.中国科学技术大学，合肥 230026；2.陕西省地震局，西安 710068；3.韩城地震台，陕西 韩城 715403）

基于遗传算法的广义回归神经网络在地震预测中的应用

韩晓飞1，2，潘存英3，罗词建2

（1.中国科学技术大学，合肥 230026；2.陕西省地震局，西安 710068；3.韩城地震台，陕西 韩城 715403）

提出了利用基于遗传算法结合广义回归神经网络（GRNN）进行地震预测的新方法。利用遗传算法的全局搜索能力、不易陷入局部极小点等优点来优化GRNN的径向基函数中心、宽度以及输出层的权值，使得计算结果全局最优。在实际地震数据中选取了100组样本数据进行仿真实验，并利用MATLAB进行仿真。仿真结果表明，本文提出的方法具有较高的精度和一定的理论指导意义。

广义回归神经网络；遗传算法；地震预测

0 引言

地震预测是对未来地震的发震时间、发震地点和震级做出预报。由于地震的孕育发生过程是一个复杂的、非线性以及不确定的动力学系统，它至今是一个世界性的科学难题，也是现代高科技的前沿课题。目前，国内外地震学家在地震预测中所使用的方法主要有以下3大类：（1）非确定性数学方法；（2）物理学方法；（3）新发展的系统科学方法。

随着计算机技术的发展和普及，以及计算机智能的迅速发展，智能化的计算方法成为研究的一个热点问题，其中包括神经网络、遗传算法、模糊控制以及专家系统等。由于神经网络具有非线性拟合能力、很强的容错性和鲁棒性，故本文采用广义回归神经网络对地震进行预测。但是由于GRNN易陷入局部最小值，进而利用遗传算法来对GRNN进行优化，从而得到全局最优值。

1 广义回归神经网络

广义回归神经网络（Generalized Regression Neural Network，简称GRNN）是美国学者Donald F.Specht在1991年提出的。它是径向基函数网络的一种，是一种三层静态前向网络，其拓扑结构如图1所示。第一层为输入层，由信号源节点组成；第二层为隐含层，其单元数根据所描述问题的需要而定；

第三层为输出层，它对输入模式的作用做出响应。

图1径向基神经元模型结构

GRNN具有很强的非线性映射能力和柔性网络结构，以及高度的容错性和鲁棒性，适于非线性问题的研究，在逼近能力和学习速度上较RBF网络有着较强的优势。网络最后收敛于样本量积聚较多的优化回归面，并且在样本数据较少时，预测效果也较好。此外，网络还可以处理不稳定的数据。利用径向基神经元和线性神经元就可以建立广义回归神经网络，其神经元模型结构如图2所示。

2 遗传算法对GRNN的优化

GRNN每个隐含层节点都有2个重要的参数，即径向基函数的中心和宽度。中心的选取对于神经网络的函数逼近能力具有很大的影响，不恰当的选取会使网络收敛慢，甚至造成网络发散；而宽度决定了网络对输入数据的响应范围。除此之外，隐含层到输出层的连接权是另外一个需要训练的参数。然而，GRNN常规的学习规则很容易使结果收敛到局部最小，甚至根本不收敛。所以采用遗传算法对GRNN进行优化，以求得全局最优值。其具体操作过程如下。

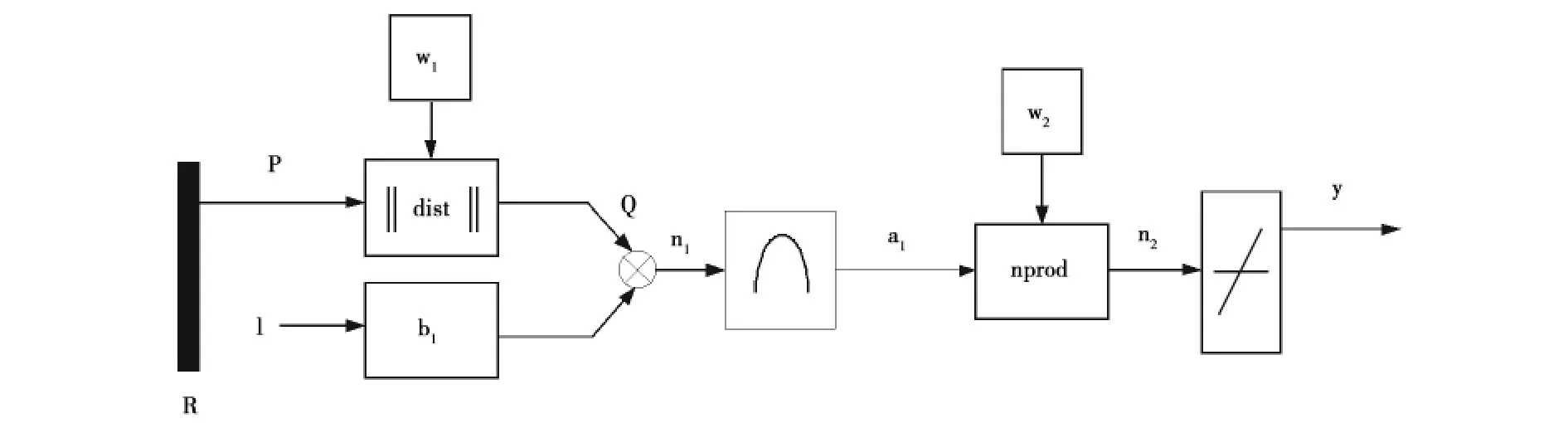
图2 广义回归神经网络结构图

2.1 编码

以往的训练方法大都属于混合方式，这种方法将聚类和获取权重分为不相关的两个独立的过程，失去了整个RBF网络的完整性。为克服上述缺点，本文将RBF网络的参数统一编码，将三种参数编到一个染色体中。对于RBF神经网络，中心是重要参数，对网络性能有很大影响，不同的中心对应着不同的宽度，中心变化，宽度也随之变化，所以采用中心和宽度交替排列的编排顺序。对于一个染色体串，具体的编码方式是：不同的中心和对应的宽度顺次排列，再顺序编排各个调节权重。同时，根据神经网络训练的精度要求，预设网络隐层节点个数P，在计算过程中根据逼近程度调整P，最终满足精度要求或精度不再提高。通常可先选择较小的P值，再不断增加。这样每个染色体串的长度为MP＋P＋NP，其中M为输入节点数，P为隐层节点数，N为输出节点数。其染色体结构图如表1所示。

表1 染色体编码串

常用的编码方式有二进制和实数编码2种。二进制编码具有编码、解码操作简单，交叉、变异操作便于实现等优点。然而二进制存在着连续函数离散化时的映射误差。个体编码串较短时，可能达不到精度要求；而个体编码串长度较长时，虽然提高编码精度，但却会使遗传算法的搜索空间急剧增大，尤其对于RBF网络这种优化参数比较多的情况，其巨大的搜索空间会使得遗传算法性能相当差，甚至无法进行下去。而实数编码（浮点数编码）是个体的每个基因值都用某一个范围内的浮点数表示，个体编码长度等于其决策变量的个数。便于在较大空间的遗传搜索，且精度高于二进制编码，因此本文采用实数编码方式。

2.2 初始种群的产生

种群的大小对遗传算法的影响很大，种群数目大，可以增加种群中个体的多样性，容易找到最优解，但会延长算法收敛的时间；种群数目小，可以加快算法的收敛，但容易陷入局部极小值。

2.3 适应度函数的构造

适应度是遗传算法中描述个体性能的主要指标。一般个体适应度取值越大，个体的性能越好；反之，个体适应度越小，个体性能越差。在遗传算法中，适应度的值必须是大于等于0的数。因此，将目标函数转换成适应度函数，一般需遵循2个基本原则：适应度值必须大于等于0；优化过程中目标函数变化（如向目标函数最大值变化或最小值变化）方向应与群体进化过程中适应度函数变化方向一致。训练RBF神经网络的目标是使网络的精确度函数达到最小，精确度由网络期望输出与实际输出之间的误差决定，因此建立适应度函数为：

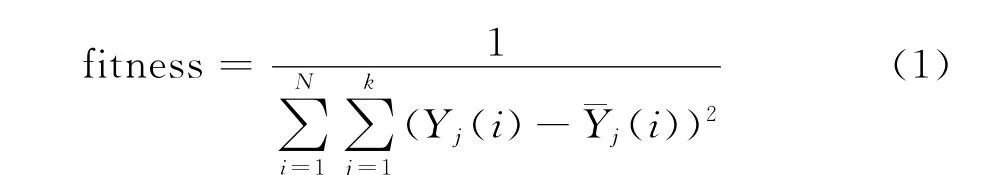
其中，Yj（i）和¯Yj（i）分别表示训练数据i在第j个输出节点的实际输出和期望输出，K和N 分别是输出节点数和输入数据的数目。

2.4 选择操作

本文的选择操作采用赌轮选择（比例选择）方法，赌轮选择是遗传算法选择操作最常用的方法。它是将所有个体的适应度之和看作一个轮盘，根据适应度的大小，将每个个体与轮盘中某些部分对应起来，然后旋转轮盘上的指针，指针所在处对应的个体被选中。应用计算机操作的具体方法是：对上代群体中所有个体的适应度进行累加得适应度之和∑F：根据各个个体的适应度值的大小，将各个个体与［0，∑F］上某区域建立对应关系；在［0，∑F］范围内产生一个随机数；随机数所在的区域对应的个体被选择。显然，个体适应度值越大，被选择的几率越大。

2.5 交叉操作

针对本文的实数编码方式，交叉操作采用3点算术交叉方案。其具体做法为：首先产生3个随机数并转换成需要进行交叉操作的实数位置。如图3中的3个随机数为3、6、9，表明将对染色体中的第3、第6和第9实数进行交叉操作。然后针对确定3对实数采用算术交叉产生下一代群体。

图3 交叉操作

算术交叉是由2个实数的线性组合而产生2个新的个体。假设对父代染色体中的Xk和Yk进行算术交叉，则交叉运算后所产生的2个实数为：

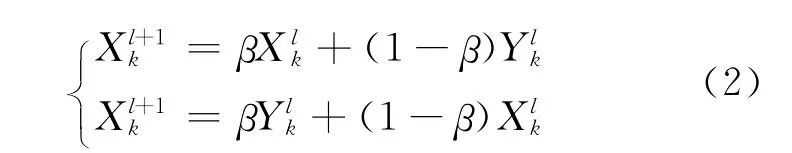
式中，β为取值范围在（0，1）内的常数，本文取交叉概率Pc＝0.6。

2.6 变异操作

在二进制编码中，被选中的变异位进行取反运算，即如果是“0”则变为“1”，如果是“1”变为“0”。但是，对于实数编码则不同于二进制编码。本文采用的是2点按位变异，首先随机生成变异点的位置（与交叉点的选取方法相同），然后在参数取值范围之内生成2个随机数，替换变异点原有的实数，替换后的新个体作为下一代染色体。

2.7 GA-GRNN算法流程设计

根据前面遗传算法优化GRNN的方法，整个地震预测模型设计流程如下：

1、对原始数据进行预处理，以达到训练要求；

2、根据确定的编码方式和种群大小，用随机数发生器，对种群进行初始化，生成初始种群P（t），并设进化代数t＝0；

3、将染色体个体进行解码操作，得出G R NN的3个重要参数，并通过G R NN的结构公式计算出输入训练样本所对应的输出；

5、找出群体中适应度值最高和最低的个体，采用最优保存策略；

6、判断适应度值是否满足收敛精度要求，如满足，则结束，如未满足，转到下一步；

7、判断当前进化代数t是否达到最大进化代数，如达到，则结束，如未达到，转到下一步；

8、对当前种群进行选择、交叉、变异操作；

9、通过遗传操作，生成新一代种群，当前进化代数t＝t＋1，转到第3步。

以上训练过程结束后，得到最终的进行地震预测的G R NN，再通过测试样本进行测试，观察计算结果与实际地震参数的误差。算法的整体流程图如图4所示。

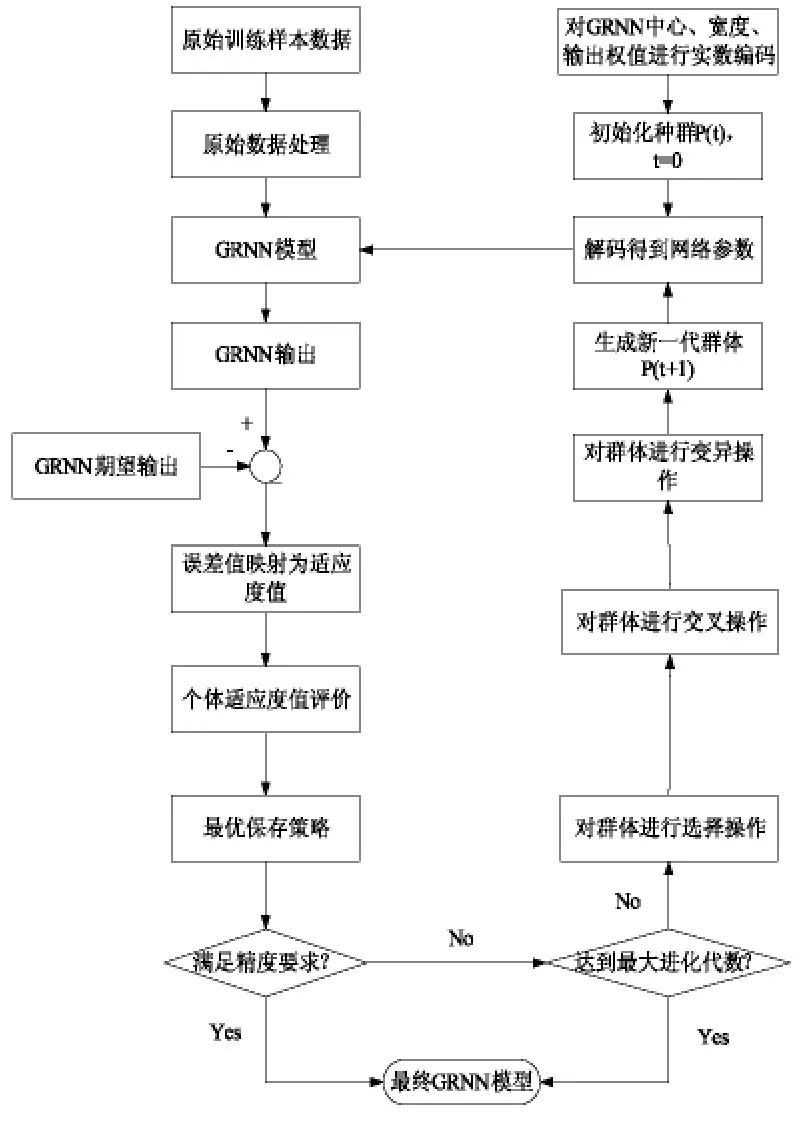
图4 算法整体流程图

3 基于MAT L A B的仿真及分析

以陕西省汉中地震台观测资料对应陕西周边地区2006—2011年的地震资料作为样本源，选择地震前3天的日均值数据作为样本数据（表2）。实现基于G R NN的地震预报。根据这些地震资料，提取出7个预报因子和实际发生的震级作为输入和目标向量。根据相关文献分析以及对地震活动前兆观测量的调查，最终选定预报因子为：（1）气氡；（2）气汞；（3）气温；（4）气压；（5）垂直摆；（6）伸缩仪；（7）水管仪。一共收集了100组样本数据，其中列出了后15组地震数据（表3）。

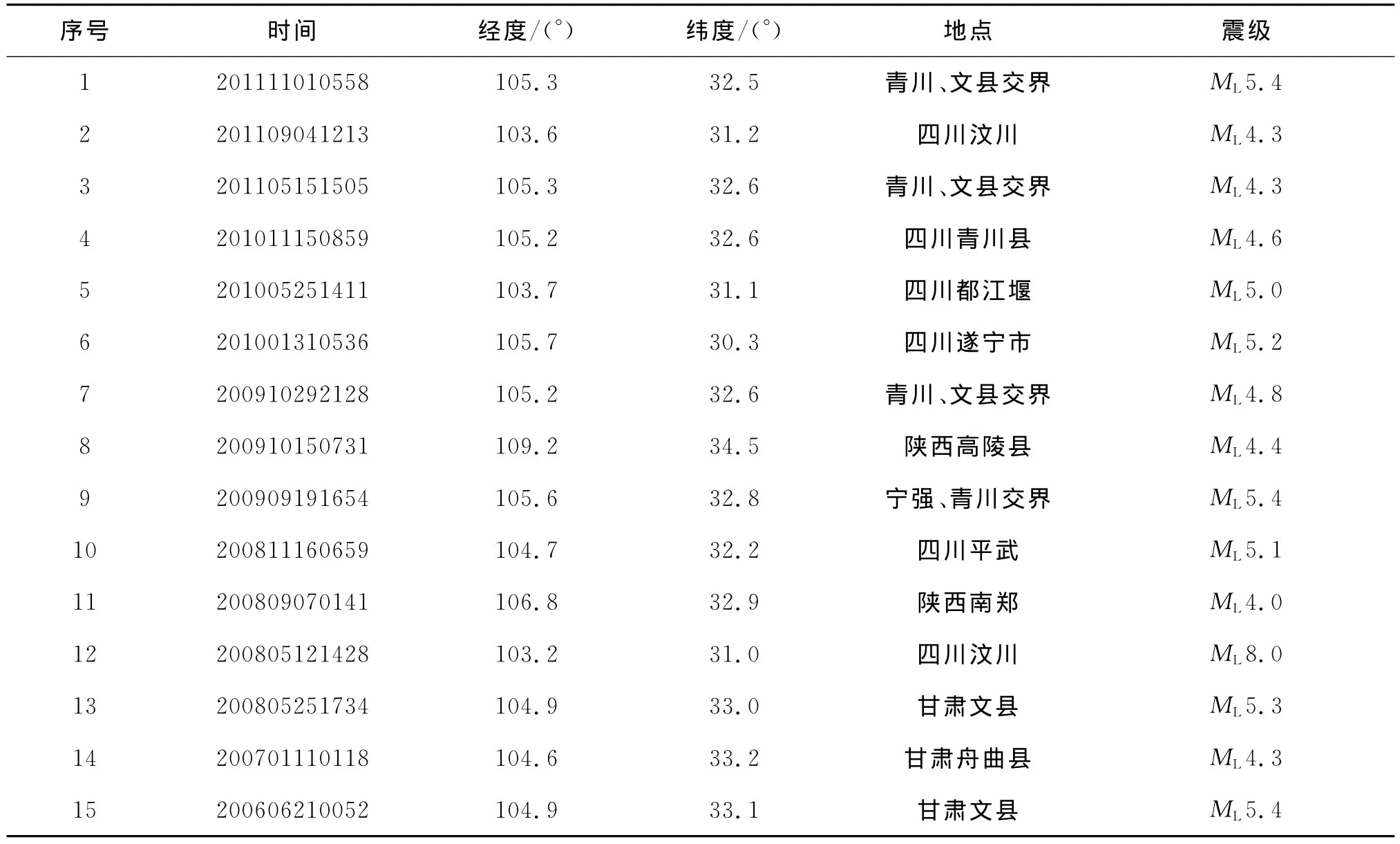
表2 地震样本

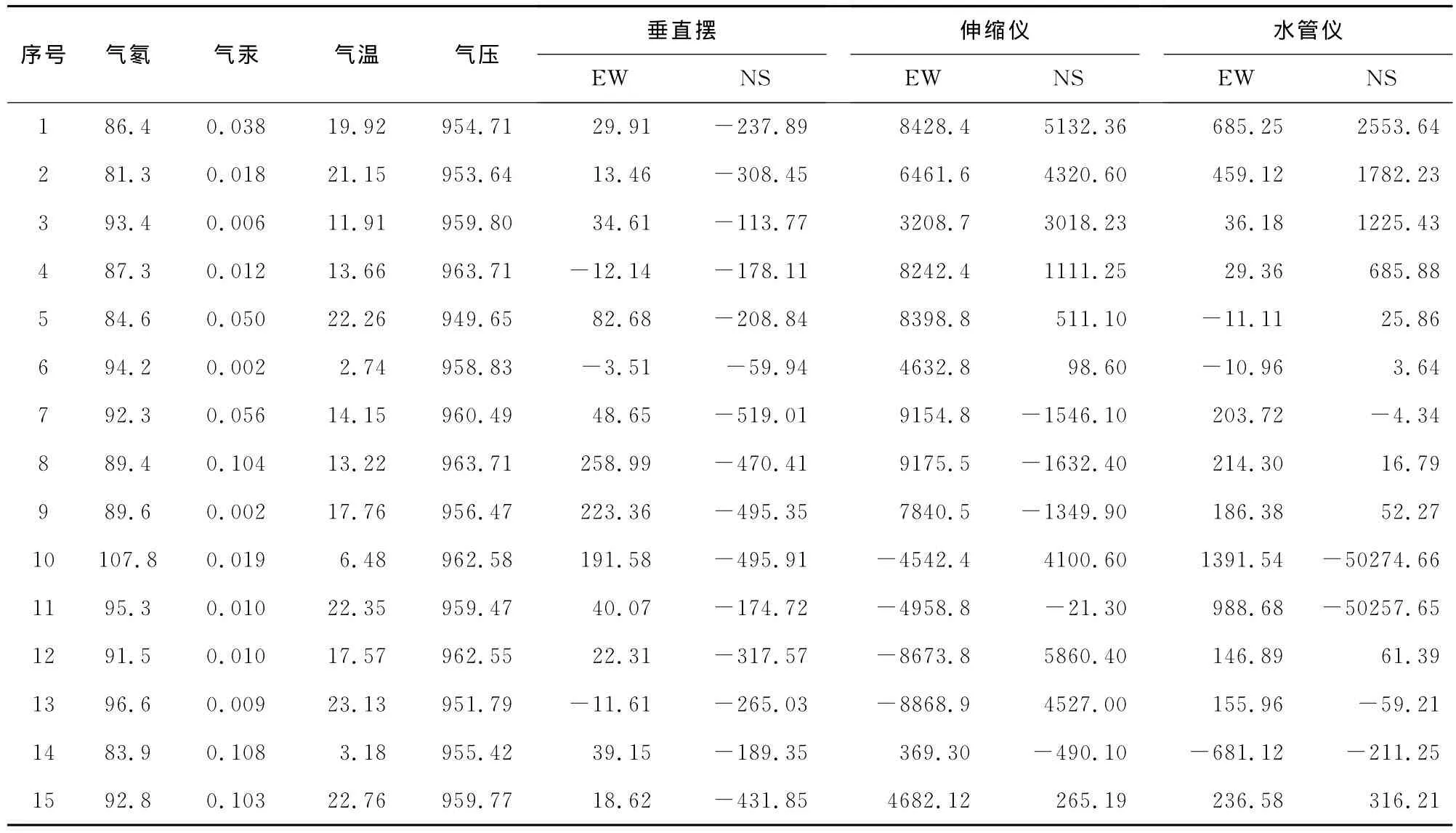
表3 学习样本

其中前95组样本数据作为训练样本，最后5组数据作为测试样本。按照上述设计步骤，建立仿真模型如下。

图5是采用BP神经网络得到的仿真图，其中图（a）是样本误差曲线，从图中可以看出经过167步，曲线误差达到0.001。（b）图‘＋’代表预测值，‘－’表示实际地震级数。（c）图是经过B P神经网络对地震进行预测后所得到的震级与实际震级的相对误差曲线。

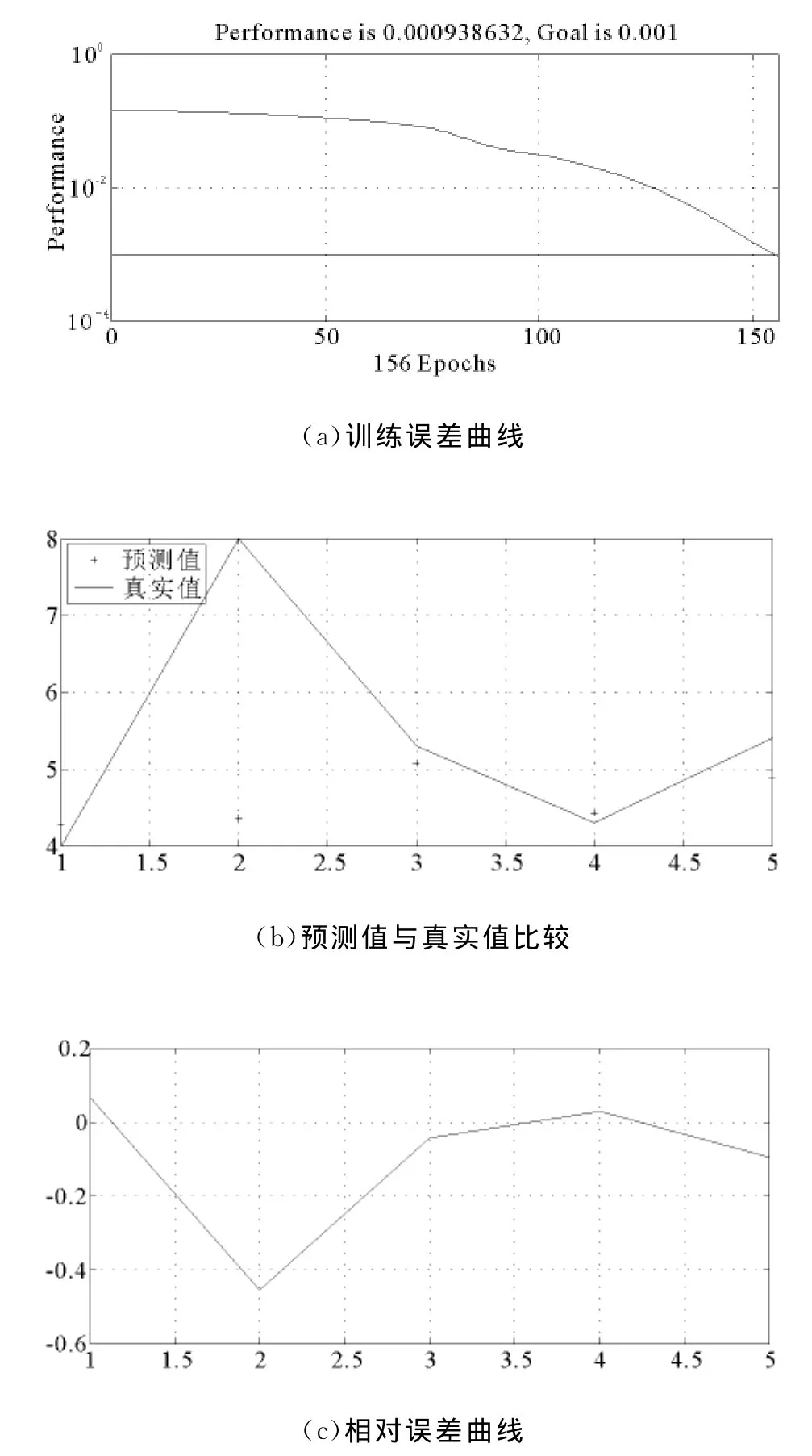
图5 BP神经网络的地震预测

图6为采用本文所介绍的GA-GRNN方法得到的仿真图，其中（a）是样本训练的误差曲线，从图中可以看出经过5步，曲线误差达到0.001。（b）图‘＋’代表预测值，‘－’表示实际地震级数。（c）图是经过B P神经网络对地震进行预测后所得到的震级与实际震级的相对误差曲线。

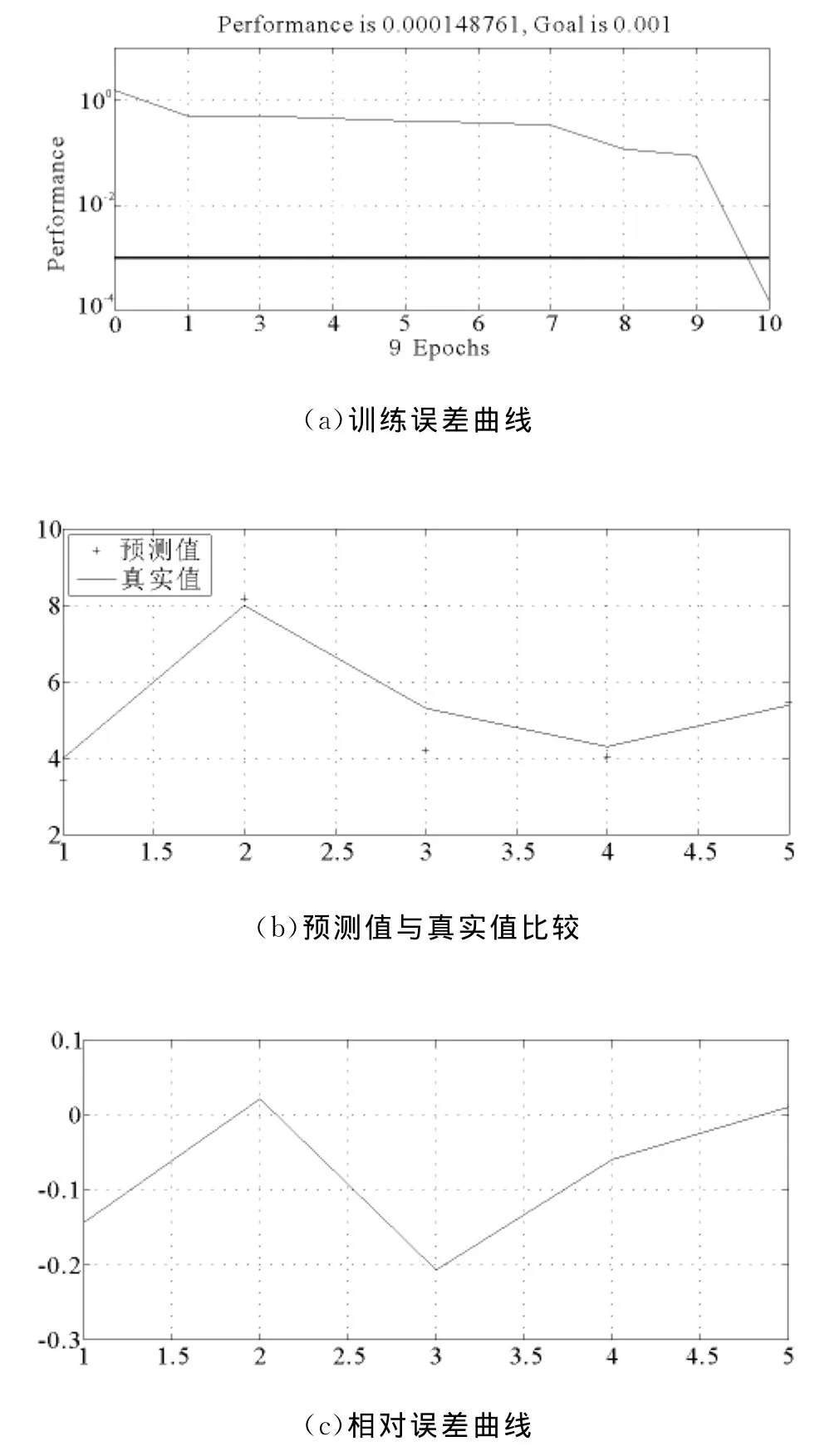
图6 GA-GRNN方法的地震预测

表4为BP算法和本文使用的GA-GRNN方法对地震预测结果的比较。

从仿真结果可以看出，本文所提出的GAGRNN方法训练步数相比BP算法大为减少，BP算法达到训练目标需要167步，而本文算法只需5步；其次，由于遗传算法的引进，使得GA-GRNN方法可以寻找到全局最优解，从地震预测的结果及预报误差分析来看，GA-GRNN方法相比BP算法有着更高的精度。

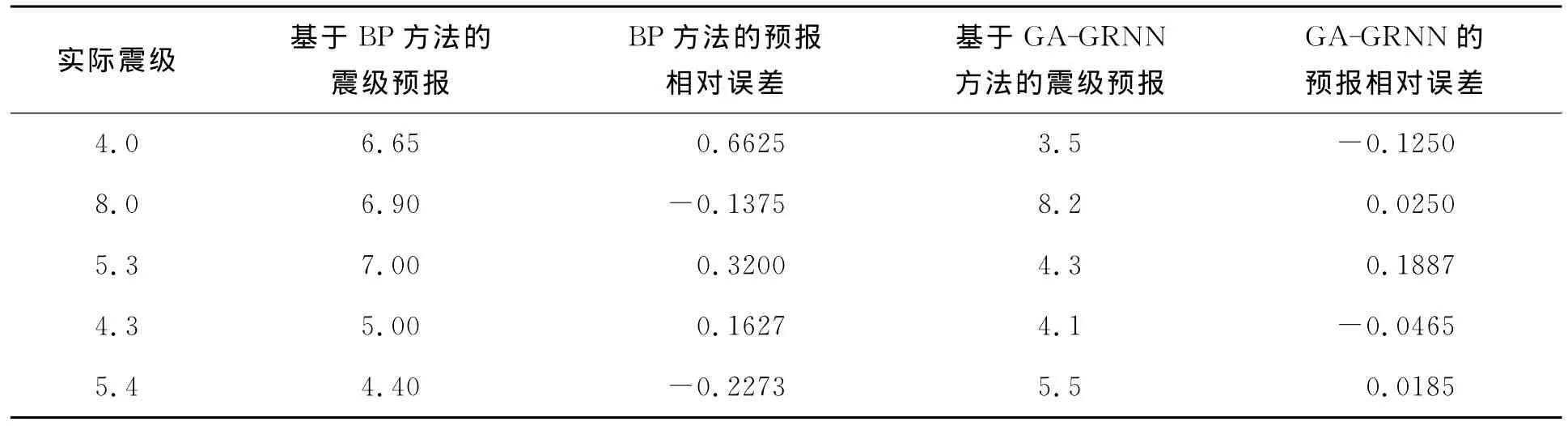
表4 B P算法与G A-G R N N方法比较

4 结论

地震预测是个世界性的科学难题，本文提出GA-GRNN方法来对地震进行预测，通过搭建B P神经网络模型以及本文所提出的GA-GRNN模型比较，说明本文所提出的GA-GRNN方法相比传统的BP法预测方法不仅可以找到全局最优解，而且有着更少的训练步数，证明了本文所提出的方法在地震预测的可行性。

［1］ 梅世蓉，冯德益.中国地震预测概论［M］.北京：地震出版社，1993.

［2］ 蒋长胜.与地震预测有关的关键物理问题［J］.国际地震动态，2007，（2）：1-8.

［3］ 王培德.对推进地震预测工作的一些政策问题的讨论［J］.国际地震动态，2009，（9）：2-10.

［4］ 国家地震局科技监测司.综合预测分册［M］.北京：地震出版社，1989.

［5］ Hung－Ming Lin，Shun－Kung Chang，Jian－Hong Wu，et al.Neural network－based model for assessing failure potential of highway slopes inthe Alishan，Taiwan Area：Pre－and post－earthquake investigation［J］.Engineering Geology.2009，104（3）：280－289.

［6］ 张国民，张晓东，吴荣辉，等.地震预测回顾与展望［J］.国际地震动态，2005，（5）：3-15.

［7］ 欧阳志远.关于地震预测预测得认识论和方法论问题［J］.中国人民大学学报，2009，（1）：96-104.

Application of Generalized Regression Neural Network Based onGenetic Algorithm in Earthquake Predication

HAN Xiao－fei 1，2，PAN Cun－ying3，LUO Ci－jian2
（1.University of Science and Technology of China，Hefei 230026，Anhui，China；2.Earthquake Administraton of Shaanxi Province，Xi’an 710068，Shaanx，China；3.Hancheng Seismic Station，Hancheng 715403，Shaanxi，China）

A new method was proposed to predict earthquake through using generalized regression neuralnetwork（GRNN）based on genetic algorithm（GA）.Global optimum can be found through using GA’s a－bility of global searching and being not liable to get the minimum to optimize the the center and width ofradial basis function and weights of output layer.At last，using100sample data obtained from actualearthquake，a simulation experiment is done based on MATLAB.The simulation shows that the methodhas a good result.

generalized regression neural network；genetic algorithm；earthquake prediction

P315.01；P315.75

A

1003－1375（2012）01－0048－06

2011-07-14

韩晓飞（1982－），男（汉族），陕西西安人，工程师﹐主要从事地震观测与研究工作.E-mail：liuyun2196＠sina.com.cn